8 Moderation & Interaktion
8.1 Folien
8.2 Daten der heutigen Sitzung
8.3 Code und Ausgaben aus der Vorlesung
Laden der relevanten Pakete
library(report) # Einfaches Erstellen von statistischen Berichten
library(marginaleffects) # Vorhersagen aus Regressionsmodellen
library(patchwork) # Mehre Plots in einer Grafik kombinieren
library(tidyverse) # Datenmanagement und Visualisierung: https://www.tidyverse.org/── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.2.0 ✔ readr 2.1.6
✔ forcats 1.0.1 ✔ stringr 1.6.0
✔ ggplot2 4.0.2 ✔ tibble 3.3.1
✔ lubridate 1.9.4 ✔ tidyr 1.3.2
✔ purrr 1.2.1
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsLesen und Aufbereiten des Datensatz von Voegele & Bachl
# https://osf.io/72azd/
d <- haven::read_sav(here::here("data/Voegele_Bachl_2017.sav")) |>
mutate(
schwab = factor(c_0001, labels = c("Hochdeutsch", "Schwäbisch")), # Stimulus
gender = as_factor(v_113), # Gender
age = ifelse(v_114 == 0, NA, v_114), # Alter
gesamt = v_126, # Gesamtbewertung des Politikers
sym = rowMeans(pick(v_139, v_141)), # Sympathie des Politikers
atol = rowMeans(pick(v_25, v_26_gedreht, v_27, v_28_gedreht, v_29)), # Einstellung zum schwäbischen Dialekt
klang = rowMeans(pick(v_54, v_55_gedreht, v_57_gedreht)), # Klang der Stimme
verst = rowMeans(pick(v_121, v_122, v_123, v_125)), # Verständlichkeit des Sprechers
polint = rowMeans(pick(v_4, v_5))
) |>
filter(v_104 == 1) |> # Filter: Nur Wahlberechtigte in BW
filter(gender != 0) |> # Zur Vereinfachung: Ohne 1 Person ohne Gender- und Age-Antwort
mutate(gender = fct_drop(gender)) |> # Zur Vereinfachung: Ohne 1 Person ohne Gender- und Age-Antwort
select(schwab, gender, age, polint, atol, klang, verst, gesamt, sym)Stichprobenbeschreibung
d |>
select(schwab, gender, age, atol, gesamt) |>
haven::zap_labels() |>
report_sample(by = "schwab")# Descriptive Statistics
Variable | Hochdeutsch (n=146) | Schwäbisch (n=177) | Total (n=323)
-------------------------------------------------------------------------------
gender [männlich], % | 44.5 | 43.5 | 44.0
Mean age (SD) | 39.34 (18.53) | 40.16 (19.10) | 39.79 (18.82)
Mean atol (SD) | 3.33 (0.77) | 3.29 (0.79) | 3.31 (0.78)
Mean gesamt (SD) | 3.84 (0.79) | 3.59 (0.90) | 3.71 (0.86)Modell ohne Interaktion mit Kontrolle von Gender schätzen
m1 <- lm(gesamt ~ schwab + gender, data = d)Regressionstabelle für Modell ohne Interaktion mit Kontrolle von Gender
m1 |>
report_table(include_effectsize = FALSE, metrics = "R2_adj")Parameter | Coefficient | 95% CI | t(320) | p | Fit
---------------------------------------------------------------------------
(Intercept) | 3.99 | [ 3.83, 4.15] | 49.21 | < .001 |
schwab [Schwäbisch] | -0.25 | [-0.44, -0.07] | -2.69 | 0.007 |
gender [männlich] | -0.33 | [-0.52, -0.15] | -3.53 | < .001 |
| | | | |
R2 (adj.) | | | | | 0.05Vorhersagen des Modells ohne Interaktion mit Kontrolle von Gender
theme_set(theme_classic(base_size = 12))
plot_predictions(m1, condition = "schwab") +
plot_predictions(m1, condition = c("schwab", "gender")) &
ylim(c(3.2, 4.2))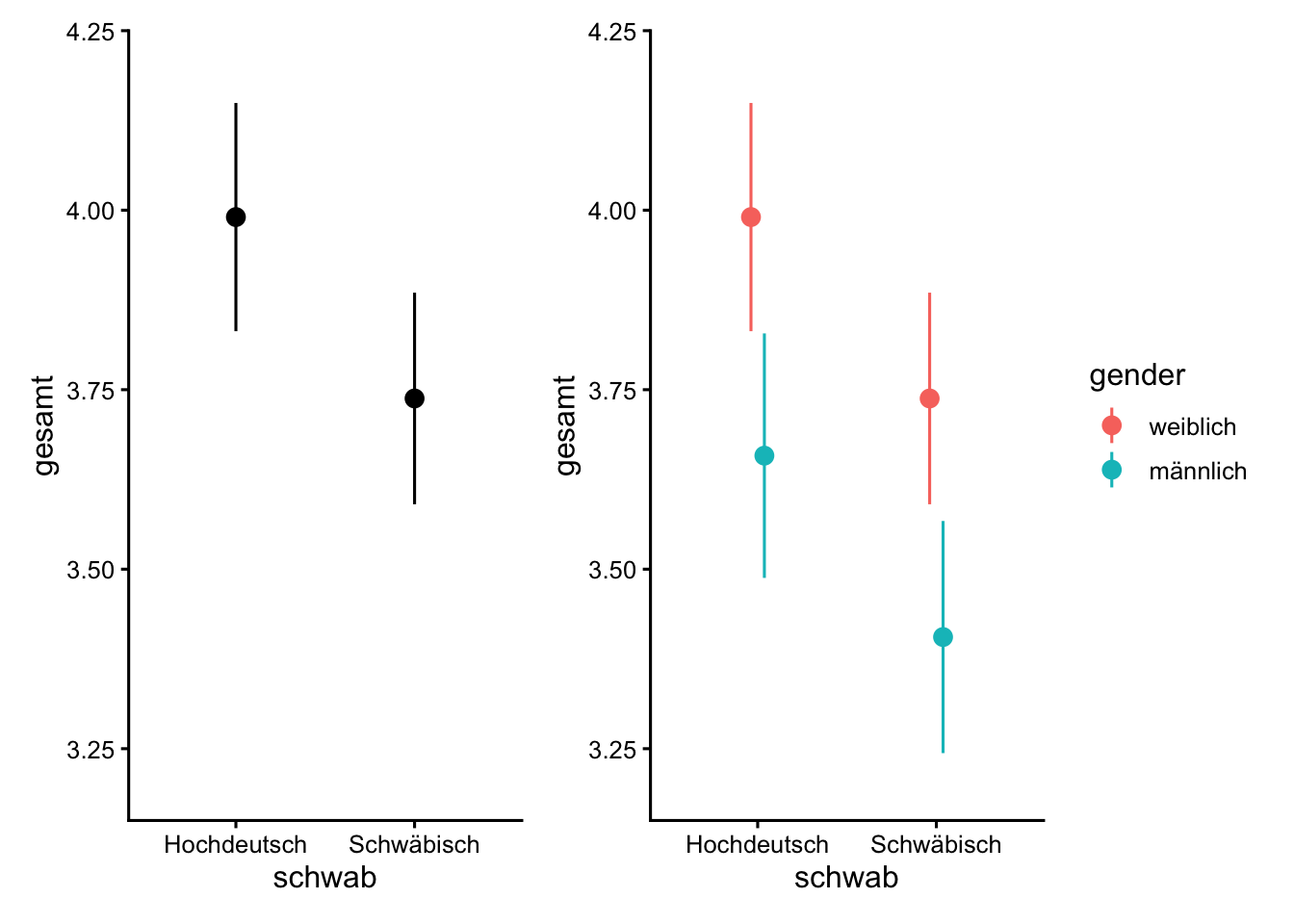
Modell mit Moderator Gender schätzen
m2 <- lm(gesamt ~ schwab * gender, data = d)Regressionstabelle für Modell mit Moderator Gender
m2_table <- m2 |>
report_table(include_effectsize = FALSE, metrics = "R2_adj")
m2_tableParameter | Coefficient | 95% CI | t(319)
-------------------------------------------------------------------------------
(Intercept) | 3.98 | [ 3.79, 4.16] | 42.58
schwab [Schwäbisch] | -0.23 | [-0.47, 0.02] | -1.79
gender [männlich] | -0.30 | [-0.57, -0.02] | -2.13
schwab [Schwäbisch] × gender [männlich] | -0.06 | [-0.43, 0.31] | -0.33
| | |
R2 (adj.) | | |
Parameter | p | Fit
-------------------------------------------------------
(Intercept) | < .001 |
schwab [Schwäbisch] | 0.074 |
gender [männlich] | 0.034 |
schwab [Schwäbisch] × gender [männlich] | 0.743 |
| |
R2 (adj.) | | 0.05Vorhersagen des Modells mit Moderator Gender
plot_predictions(m2, condition = c("schwab", "gender")) +
plot_predictions(m2, condition = rev(c("schwab", "gender"))) +
scale_color_brewer(type = "qual") &
theme(legend.position = "bottom") &
ylim(c(3.2, 4.2))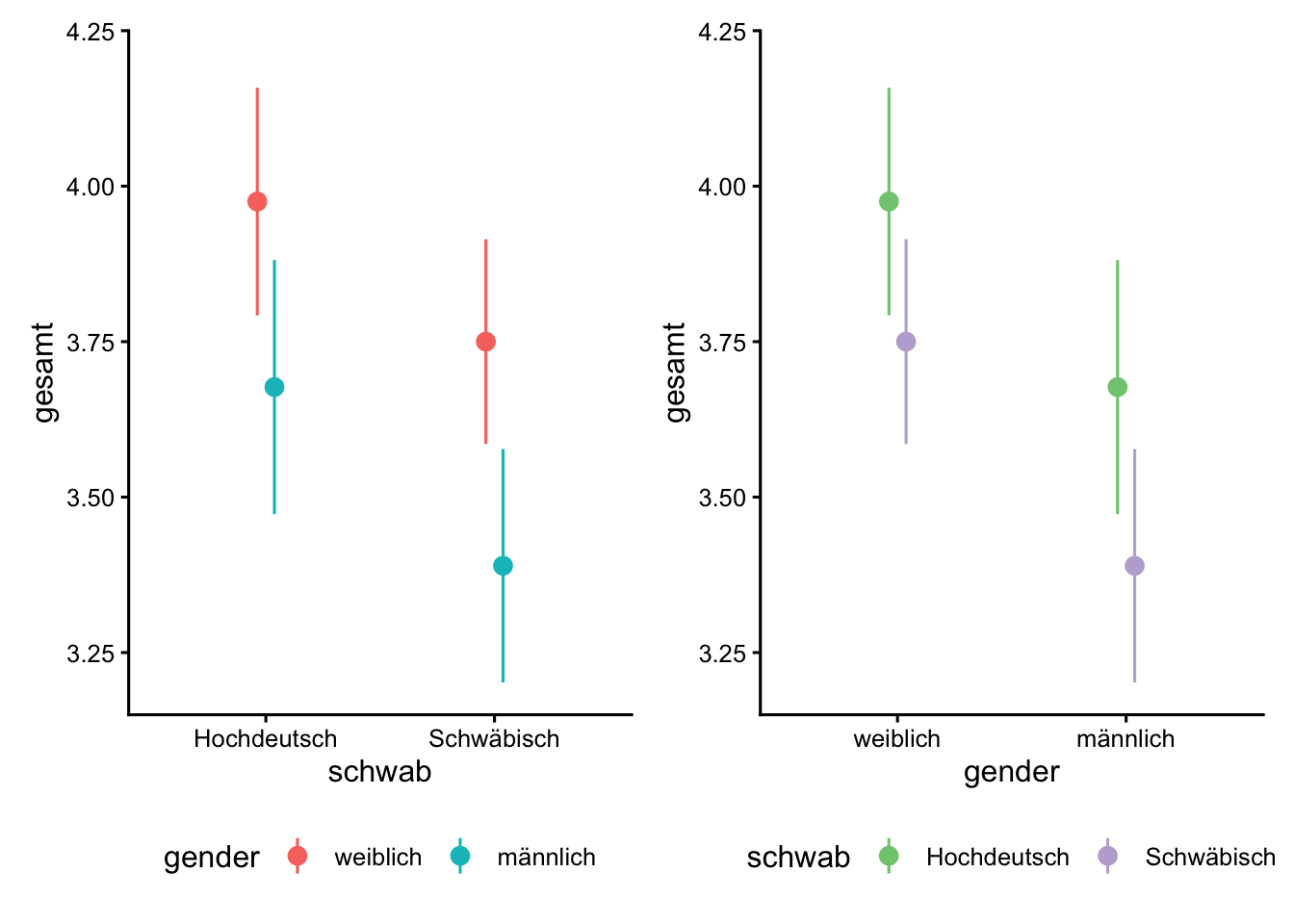
Modell ohne Interaktion mit Kontrolle von AtoL schätzen
m3 <- lm(gesamt ~ schwab + atol, data = d)Regressionstabelle für Modell ohne Interaktion mit Kontrolle von AtoL
m3 |>
report_table(include_effectsize = FALSE, metrics = "R2_adj")Parameter | Coefficient | 95% CI | t(320) | p | Fit
---------------------------------------------------------------------------
(Intercept) | 3.41 | [ 2.99, 3.83] | 15.93 | < .001 |
schwab [Schwäbisch] | -0.24 | [-0.43, -0.06] | -2.56 | 0.011 |
atol | 0.13 | [ 0.01, 0.25] | 2.12 | 0.034 |
| | | | |
R2 (adj.) | | | | | 0.03Vorhersagen des Modells ohne Interaktion mit Kontrolle von AtoL
plot_predictions(m3, condition = list("schwab", atol = "threenum")) +
plot_predictions(m3, condition = rev(list("schwab", atol = "threenum"))) +
scale_color_brewer(type = "qual") &
theme(legend.position = "bottom") &
ylim(c(3.2, 4.2))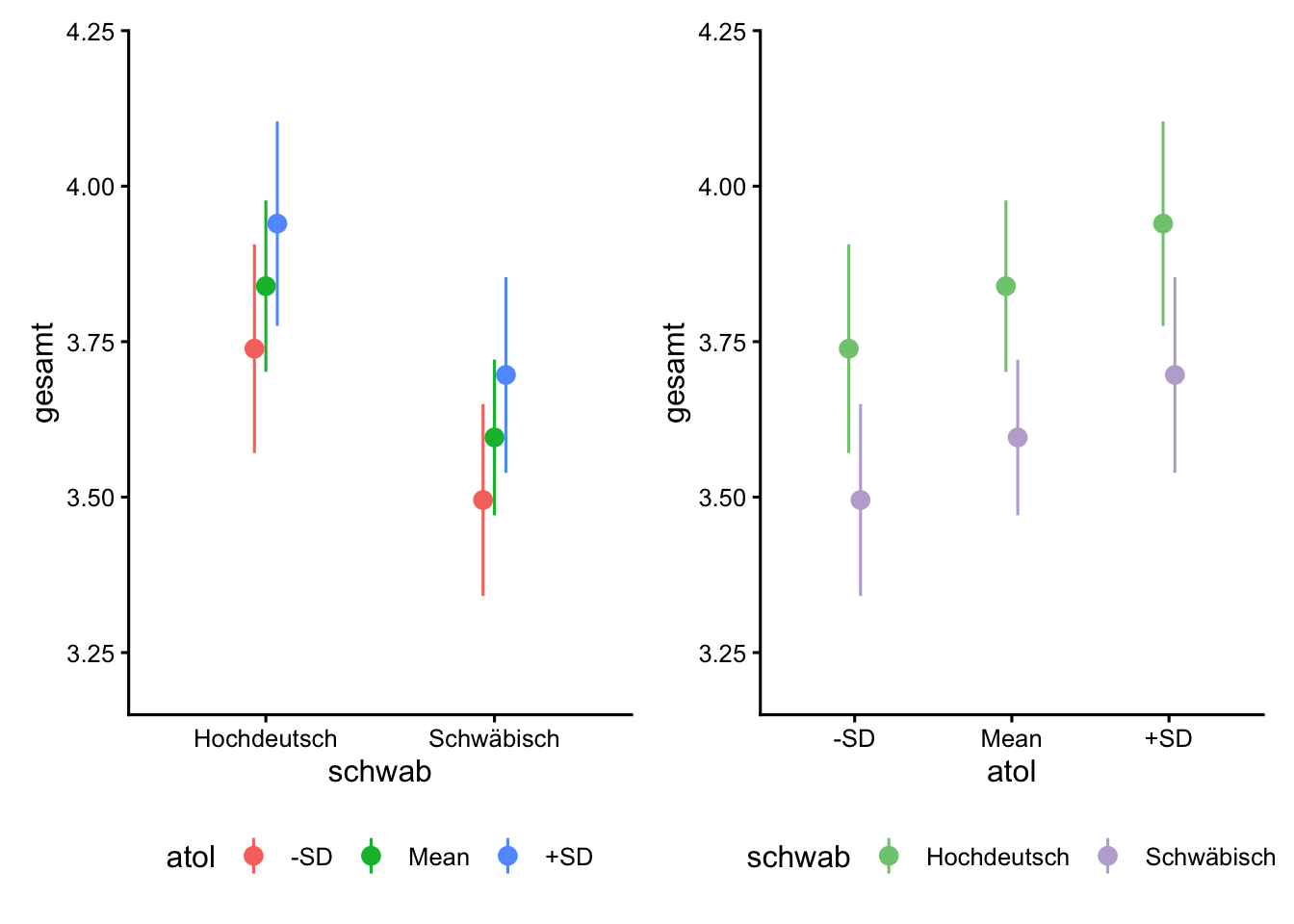
Modell mit Moderator AtoL schätzen
m4 <- lm(gesamt ~ schwab * atol, data = d)Regressionstabelle für Modell mit Moderator AtoL
m4 |>
report_table(include_effectsize = FALSE, metrics = "R2_adj")Parameter | Coefficient | 95% CI | t(319) | p | Fit
----------------------------------------------------------------------------------
(Intercept) | 4.06 | [ 3.45, 4.66] | 13.11 | < .001 |
schwab [Schwäbisch] | -1.39 | [-2.20, -0.58] | -3.37 | < .001 |
atol | -0.06 | [-0.24, 0.11] | -0.71 | 0.481 |
schwab [Schwäbisch] × atol | 0.34 | [ 0.11, 0.58] | 2.85 | 0.005 |
| | | | |
R2 (adj.) | | | | | 0.05AtoL zentrieren und Modell mit Moderation erneut schätzen
d <- d |> mutate(atol_c = atol - mean(atol))
m4_c <- lm(gesamt ~ schwab * atol_c, data = d)Regressionstabelle für Modell mit zentriertem AtoL als Moderator
m4_c_table <- m4_c |>
report_table(include_effectsize = FALSE, metrics = "R2_adj")
m4_c_tableParameter | Coefficient | 95% CI | t(319) | p | Fit
------------------------------------------------------------------------------------
(Intercept) | 3.84 | [ 3.71, 3.98] | 55.26 | < .001 |
schwab [Schwäbisch] | -0.24 | [-0.43, -0.06] | -2.61 | 0.010 |
atol c | -0.06 | [-0.24, 0.11] | -0.71 | 0.481 |
schwab [Schwäbisch] × atol c | 0.34 | [ 0.11, 0.58] | 2.85 | 0.005 |
| | | | |
R2 (adj.) | | | | | 0.05Vorhersagen des Modells mit zentriertem Moderator AtoL
plot_predictions(m4_c, condition = list("schwab", atol_c = "threenum")) +
plot_predictions(m4_c, condition = rev(list("schwab", atol_c = "threenum"))) +
scale_color_brewer(type = "qual") &
theme(legend.position = "bottom") &
ylim(c(3.2, 4.2))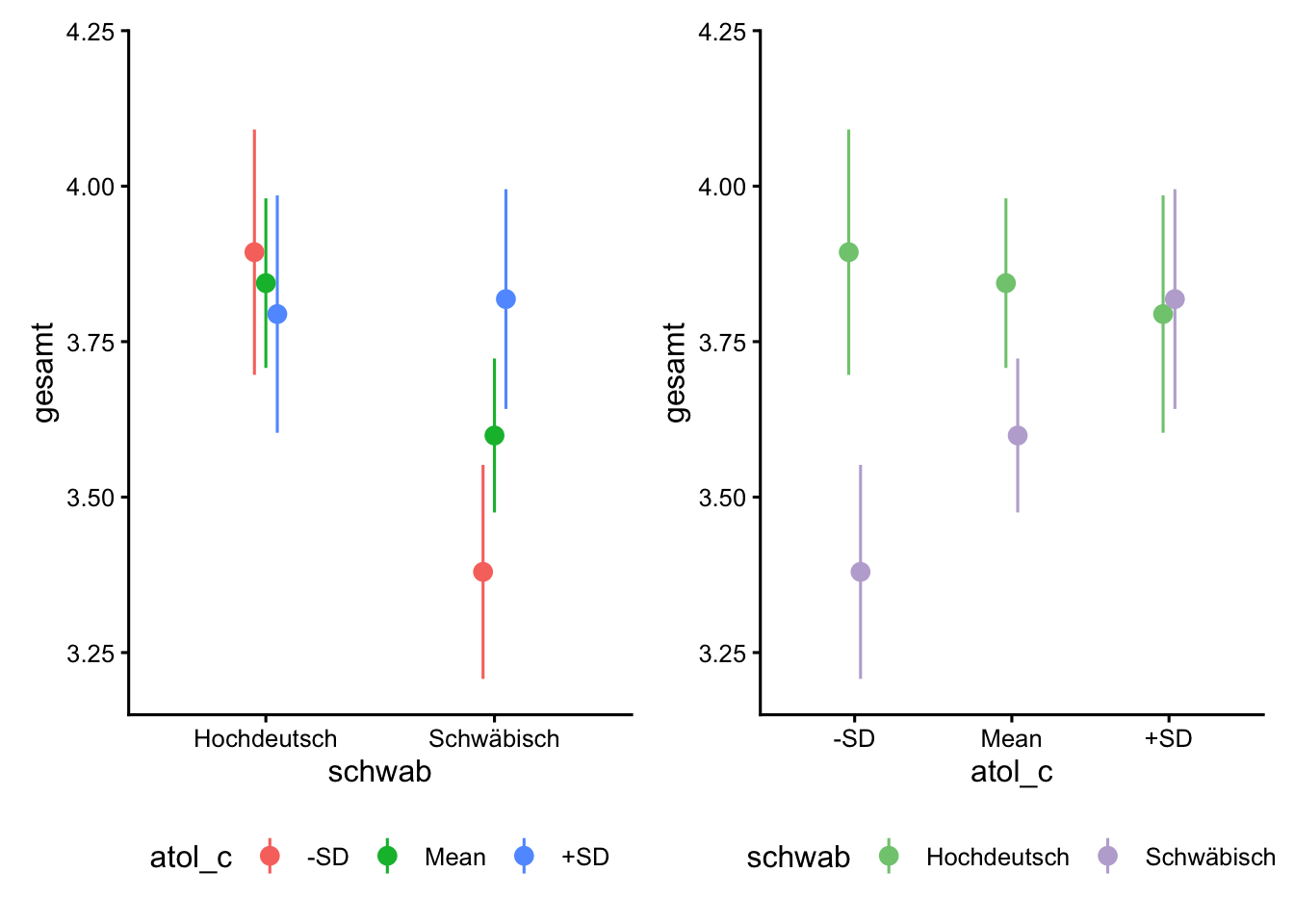
plot_slopes(m4_c, variables = "schwab", condition = "atol_c") +
geom_hline(yintercept = 0, linetype = 2)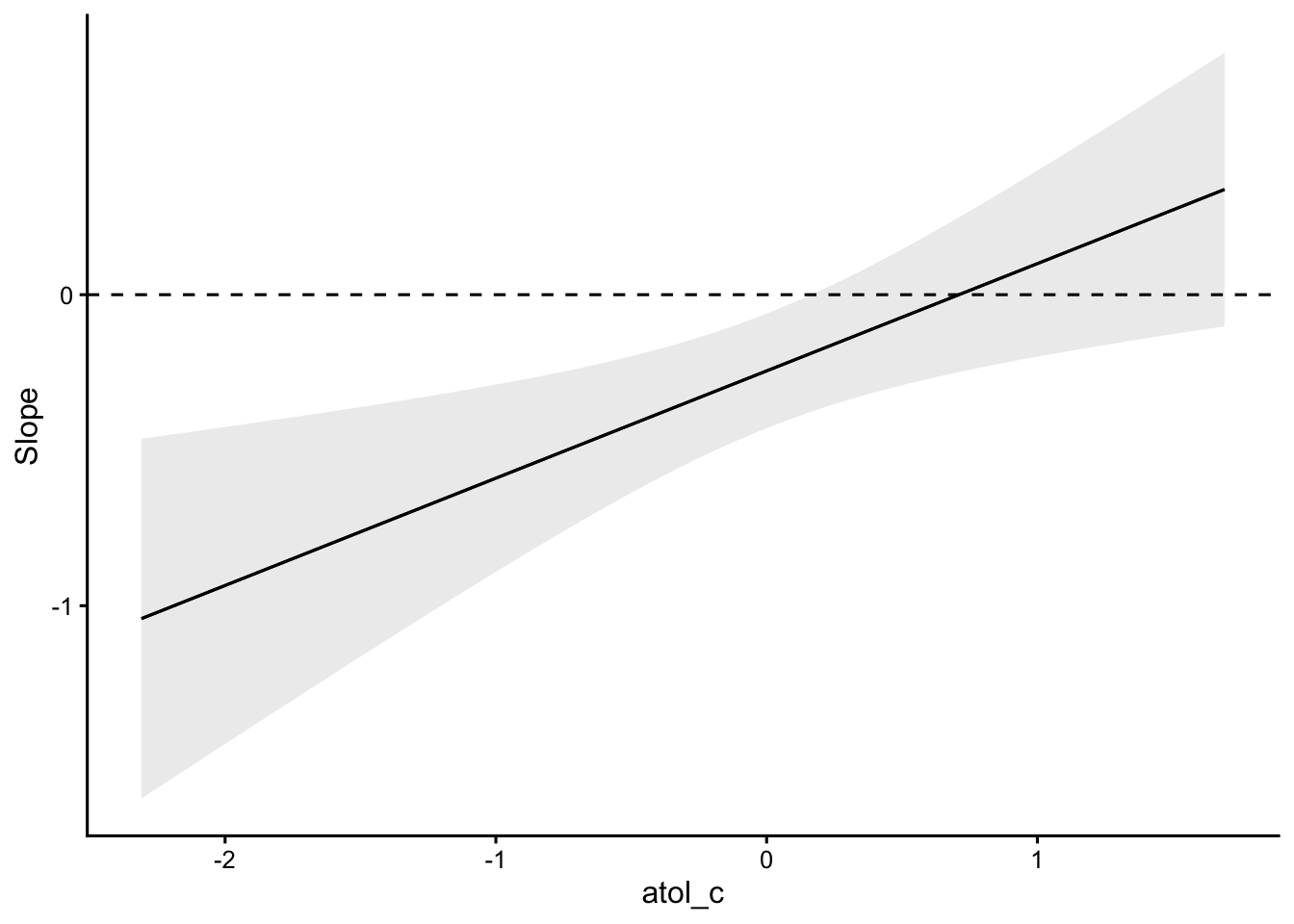
m4_c_tableParameter | Coefficient | 95% CI | t(319) | p | Fit
------------------------------------------------------------------------------------
(Intercept) | 3.84 | [ 3.71, 3.98] | 55.26 | < .001 |
schwab [Schwäbisch] | -0.24 | [-0.43, -0.06] | -2.61 | 0.010 |
atol c | -0.06 | [-0.24, 0.11] | -0.71 | 0.481 |
schwab [Schwäbisch] × atol c | 0.34 | [ 0.11, 0.58] | 2.85 | 0.005 |
| | | | |
R2 (adj.) | | | | | 0.05plot_predictions(m4_c, condition = rev(list("schwab", atol_c = "threenum")))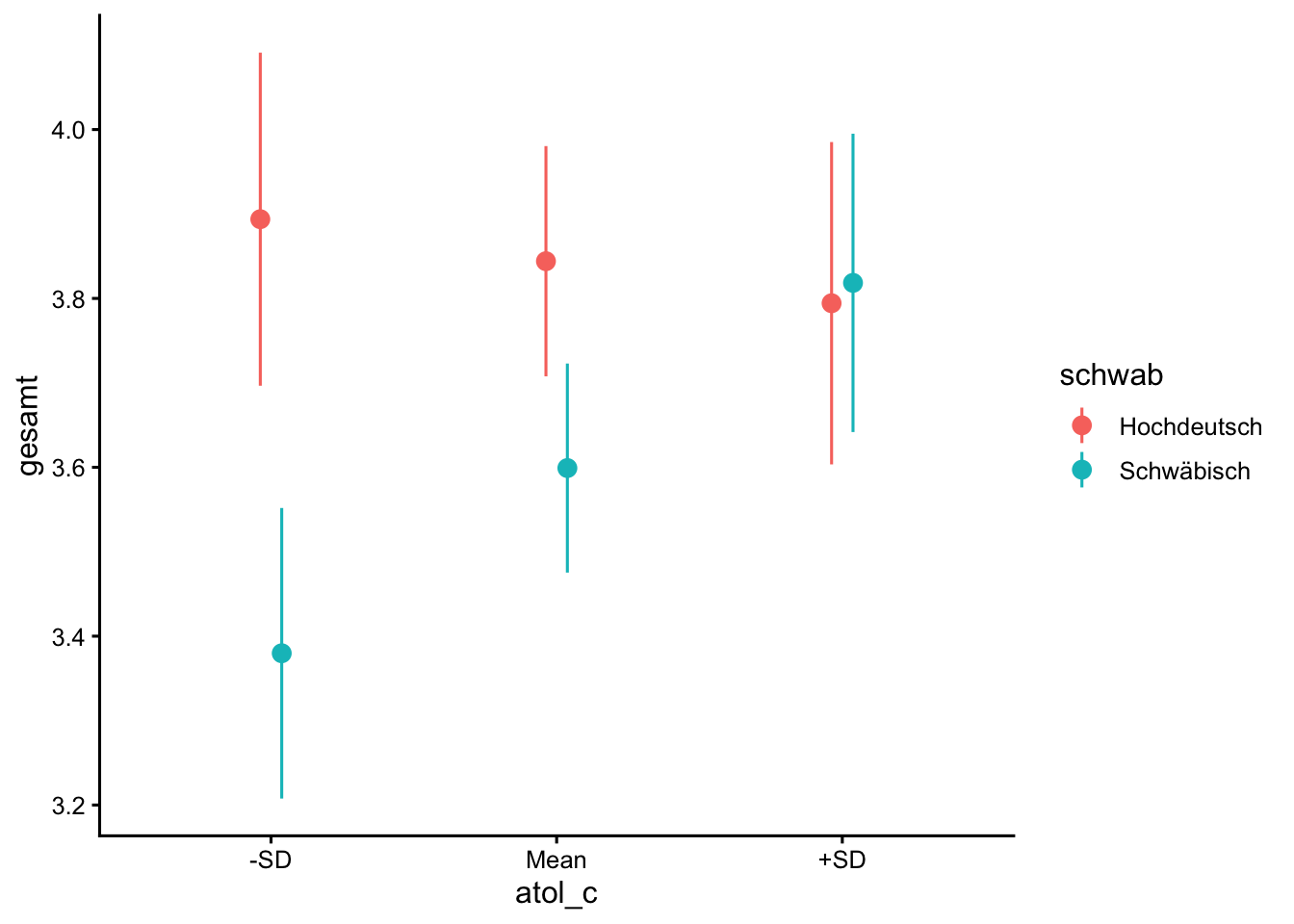
plot_slopes(m4_c, variables = "schwab", condition = "atol_c") +
geom_hline(yintercept = 0, linetype = 2)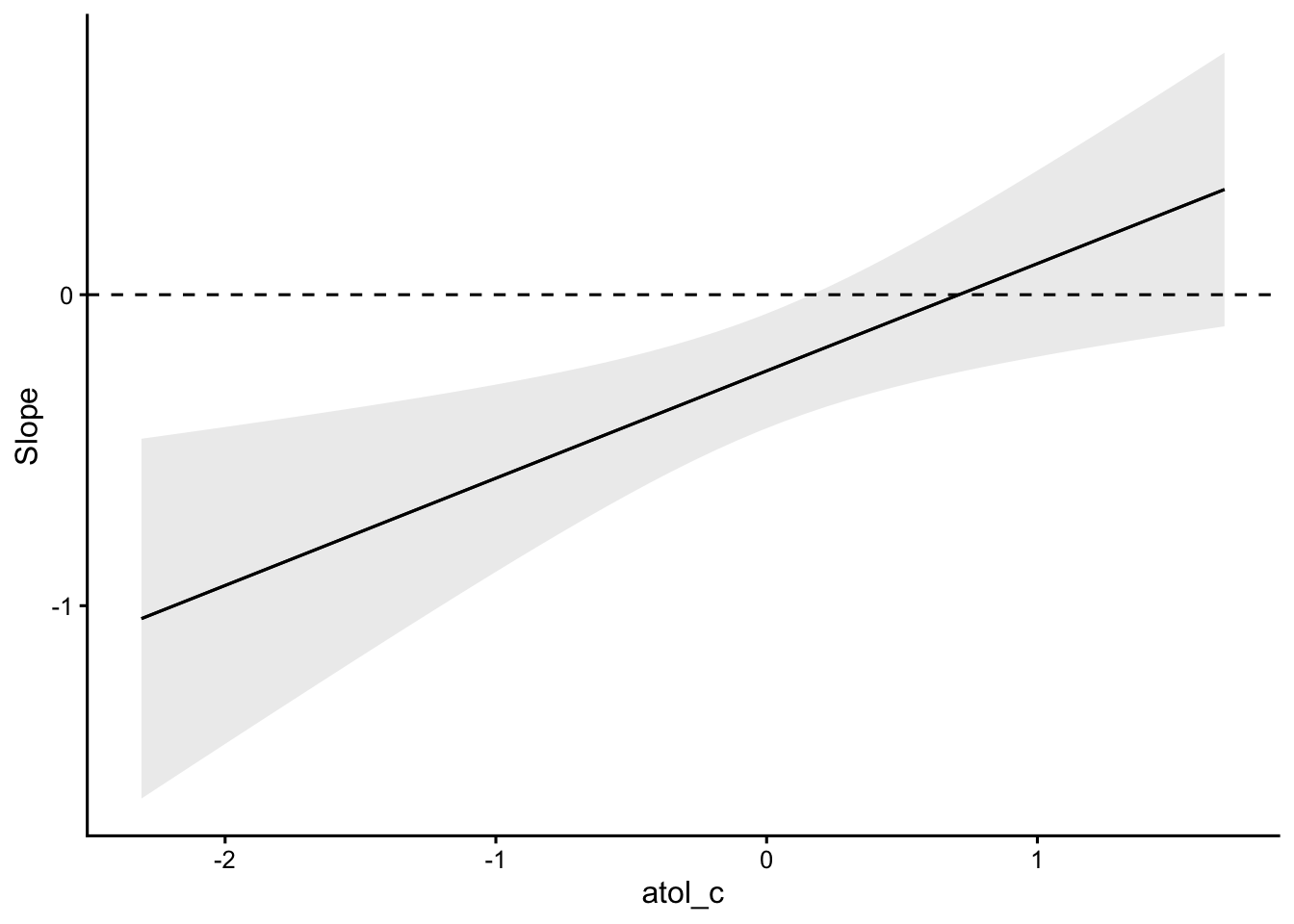
8.4 Hausaufgabe
1) Vollziehen Sie die Analysen nach, deren Ausgaben wir in der Vorlesung besprochen haben.
- Schreiben Sie kurze Ergebnistexte zur Beantwortung der Fragen bzw. zum Test der Hypothesen:
- Unterscheidet sich der Effekt des Dialekts auf die Gesamtbewertung des Politikers in Abhängigkeit des Genders der Zuhörenden?
- Je positiver die Einstellung zum schwäbischen Dialekt bei einer Versuchsperson, desto positiver (bzw. weniger negativ) ist der Effekt des Dialekts auf die Bewertung des Politikers.
- Bei Personen, die dem Schwäbischen sehr negativ gegenüberstehen, hat der schwäbische Dialekt einen negativen Effekt auf die Gesamtbewertung des Politikers.
2) Modifizieren Sie die Moderationsanalysen aus der Vorlesung.
Weitere mögliche Moderatoren neben der Einstellung gegenüber dem Schwäbischen (atol) sind Alter (age) und politisches Interesse (polint). Weitere mögliche abhängige Variablen sind der wahrgenommene Klang der Stimme (klang), die Verständlichkeit des Sprechers (verst) und die Sympathie-Bewertung des Politikers (sym). Formulieren Sie passende Hypothesen oder Forschungsfragen. Führen Sie notwendige Transformationen durch. Schätzen Sie dann das Regressionsmodell mit angepassten Variablen und erstellen Sie geeignete Grafiken. Interpretieren Sie die Ergebnisse in einigen Sätzen.
Lösung
- Zu 1) Siehe Code und Ausgaben aus der Vorlesung
- Zu 2) R Skript | HTML mit Output
8.5 Transkript
WarnungHinweise zum automatisiert erstellten Transkript
Das folgende Transkript wurde auf Basis der Aufzeichnung der Vorlesung erstellt. Die vollständigen Aufzeichnungen inklusive der Bildschirminhalte sind in Blackboard🔒 verfügbar. Die Tonspur wurde zuerst mit Hilfe der Werkzeuge des Oral-History.Digital Projekts wörtlich transkribiert. Die wörtliche Transkription wurde in Kombination mit den Vorlesungsfolien mithilfe von Sprachmodellen (v. a. Claude Sonnet 4.5 und GPT 5.2) zu einem übersichtlichen Transkript zusammengefasst. Im Anschluss wurde das Transkript von einer studentischen Hilfskraft überprüft, geglättet und ggf. angepasst. In diesem Prozess kann es an verschiedenen Stellen zu Fehlern kommen. Im Zweifel gilt das gesprochene Wort, und auch beim Vortrag mache ich Fehler.
Ich stelle das Transkript hier als experimentelles, ergänzendes Material zur Dokumentation der Vorlesung zur Verfügung. Noch bin ich mir unsicher, ob es eine sinnvolle Ergänzung ist und behalte mir vor, es weiter zu bearbeiten oder zu löschen.
Moderation und Interaktion
In dieser Sitzung geht es darum, dass Regressionskoeffizienten nicht für alle Personen gleich sein müssen, sondern sich in Abhängigkeit von einer weiteren Variable verändern können. Genau das wird als Moderation oder Interaktion beschrieben. Die Vorlesung knüpft an die vorige Einheit zur multiplen linearen Regression an und zeigt, wie man dort die Annahme aufhebt, dass Effekte für alle Fälle identisch sind.
- Zentrales Thema: Effekte können von einer anderen Variable abhängen.
- Begriffe: Moderation und Interaktion werden meist synonym verwendet.
- Fokus der Vorlesung: zweifache Interaktionen.
Was ist ein moderierter Effekt?
Ein moderierter Effekt liegt vor, wenn der Effekt eines Prädiktors auf eine abhängige Variable davon abhängt, wie eine zweite Variable ausgeprägt ist. Damit wird die einfache Additivitätsannahme der linearen Regression eingeschränkt. Als Beispiel wird die Wissensklufthypothese herangezogen: Mediennutzung kann stärker zum Wissen beitragen, wenn Menschen bereits über mehr Bildung und Vorwissen verfügen.
- Moderation bedeutet: Der Effekt von \(X\) verändert sich mit \(Z\).
- In der Medienwirkungsforschung ist das ein klassischer Fall für differenzielle Effekte.
- Die Wissensklufthypothese illustriert, dass Lernen aus Medien nicht für alle gleich stark ausfällt.
Wissenskluft
Die Wissensklufthypothese besagt, dass sich Wissensunterschiede zwischen sozialen Gruppen, vor allem nach Bildung, durch Mediennutzung eher vergrößern können. Menschen mit höherer Bildung und mehr Vorwissen lernen aus denselben Medieninhalten oft mehr als Personen mit geringerer Bildung. Die Vorlesung verweist dazu auf die klassische Studie von Tichenor et al., in der sich zeigte, dass zusätzliche Informationsangebote stärker bei besser Gebildeten wirken.
- Bildung ist ein zentraler Faktor der Wissenskluft.
- Medien können bestehende Unterschiede verstärken.
- Der Effekt von Informationszugang ist nicht für alle gleich groß.
Interaktion und Moderation
Die Begriffe Interaktion und Moderation werden in der Vorlesung weitgehend synonym verwendet, auch wenn es in verschiedenen Forschungstraditionen leichte Bedeutungsunterschiede gibt. In experimentellen Designs spricht man eher von Interaktion zwischen Faktoren, bei gemessenen Drittvariablen eher von Moderation. Ein Effect Modifier ist eine Variable, die selbst keinen kausalen Effekt haben muss, aber den Effekt einer anderen Variable verändert.
- Interaktion: gemeinsames Auftreten zweier Variablen verändert den Effekt.
- Moderation: der Effekt eines Prädiktors hängt von einem Moderator ab.
- Effect modifier: der Moderator verändert den Effekt, ohne selbst zwingend kausal zu wirken.
Aktuelle Debatten
Die genannten Modelle stehen genau für diese Entwicklung:
- Resonance Model of Political Campaign Effects: Politische Botschaften wirken nicht bei allen gleich, sondern je nach Zielgruppe unterschiedlich.
- Differential Susceptibility to Media Effects Model: Manche Menschen sind für Medienwirkungen stärker anfällig als andere.
- Person-Specific Media Effects: Medienwirkungen können sogar von Person zu Person sehr unterschiedlich sein.
Der wichtige Punkt ist also: Medien wirken nicht immer gleich, sondern oft abhängig von bestimmten Voraussetzungen. Das nennt man Effektheterogenität.
Die Warnung der Vorlesung ist aber: Solche Interaktionsmodelle sehen zwar oft elegant aus, werden in der Praxis aber leicht zu schnell oder zu einfach interpretiert. Ein signifikanter Interaktionseffekt bedeutet nicht automatisch, dass man die Theorie schon vollständig verstanden hat.
Regressionsgleichung
Die statistische Idee ist einfach: Zu einer Regressionsgleichung mit zwei Prädiktoren wird ein zusätzlicher Term eingefügt, der aus dem Produkt beider Variablen besteht. Dadurch wird modelliert, dass der Effekt von \(X\) auf \(Y\) von \(Z\) abhängt. Der neue Term heißt Interaktionsterm und wird mit einem zusätzlichen Regressionskoeffizienten geschätzt.
\[Y = b_0 + b_1X + b_2Z\]
\[Y = b_0 + b_1X + b_2Z + b_3XZ\]
- Grundform: \(Y = b_0 + b_1X + b_2Z\).
- Mit Moderation: zusätzlicher Term \(b_3XZ\).
- Der Interaktionsterm ist das Produkt von \(X\) und \(Z\).
Bedeutung der Koeffizienten
Mit Interaktion ändern sich die Bedeutungen der Regressionskoeffizienten. Die Vorlesung erklärt das über den Fall, dass bestimmte Variablen den Wert \(0\) haben. Der Intercept ist der erwartete Wert von \(Y\), wenn beide Prädiktoren \(0\) sind. \(b_1\) ist dann der Effekt von \(X\), wenn \(Z=0\), und \(b_2\) ist der Effekt von \(Z\), wenn \(X=0\). \(b_3\) beschreibt den eigentlichen Interaktionseffekt, also wie stark sich der Effekt von \(X\) verändert, wenn \(Z\) um eine Einheit steigt.
- \(b_0\): erwarteter Wert bei \(X=0\) und \(Z=0\).
- \(b_1\): konditionaler Effekt von \(X\) bei \(Z=0\).
- \(b_2\): konditionaler Effekt von \(Z\) bei \(X=0\).
- \(b_3\): Unterschied der Effekte, also die Interaktion.
Die lineare Funktion des Effekts wird dabei so geschrieben:
\[f(Z) = b_1 + b_3Z\]
Interpretation
Wichtig ist, dass Koeffizienten mit Interaktion nicht mehr unabhängig voneinander interpretiert werden können. Man muss immer fragen, für welchen Wert der jeweils anderen Variablen der Effekt gilt. Es wird außerdem betont, dass man nicht nur die Signifikanz des Interaktionsterms berichten sollte, sondern auch Richtung und Stärke der Effekte sowie Visualisierungen der Modellvorhersagen.
- Koeffizienten sind konditional und nicht allgemein gültig.
- Der Wert \(0\) muss für beteiligte Variablen sinnvoll interpretierbar sein.
- Substanzielle Interpretation ist wichtiger als nur ein Signifikanzsternchen.
Beispielstudie
Als Beispiel dient eine Studie zum Einfluss des schwäbischen Dialekts auf die Bewertung eines Politikers. Die Idee: Ob Dialekt positiv oder negativ wirkt, hängt vermutlich von der Person ab, die zuhört. Dazu wurden zwei Versionen eines Radiointerviews erstellt, einmal in Hochdeutsch und einmal in Schwäbisch.
- Treatment: Hochdeutsch vs. Schwäbisch.
- Abhängige Variable: Gesamtbewertung des Politikers.
- Moderatoren: Geschlecht und Einstellung zum Schwäbischen.
Dichotomer Moderator
Zuerst wird ein binärer Moderator betrachtet: das Geschlecht der Versuchspersonen. Ohne Interaktion zeigt sich ein negativer Effekt des Schwäbischen auf die Bewertung des Politikers sowie ein Unterschied zwischen Männern und Frauen. Mit Interaktion wird geprüft, ob der Dialekteffekt für Männer und Frauen unterschiedlich stark ist.
- Schwäbisch wird insgesamt schlechter bewertet als Hochdeutsch.
- Männer bewerten den Politiker insgesamt etwas schlechter als Frauen.
- Der Interaktionseffekt mit Gender ist nicht signifikant.
Interpretation Gender
Das bedeutet: Der negative Effekt des schwäbischen Dialekts unterscheidet sich in der Stichprobe nicht statistisch gesichert zwischen Männern und Frauen. Deshalb kann man nicht sagen, dass der Dialekteffekt für ein Geschlecht anders ausfällt als für das andere, auch wenn sich die Mittelwerte deskriptiv leicht unterscheiden.
- Kein signifikanter Unterschied des Dialekteffekts zwischen den Geschlechtern.
- Die Haupteffekte behalten eine konditionale Bedeutung.
- Der Effekt von „männlich“ gilt hier für die Hochdeutsch-Gruppe.
Quasi-metrischer Moderator
Anschließend wird die Einstellung zum Schwäbischen als metrischer Moderator betrachtet. Die Hypothese lautet: Je positiver jemand dem Schwäbischen gegenübersteht, desto weniger negativ sollte der Dialekteffekt auf die Politikerbewertung ausfallen.
- Moderator: Attitude toward language, hier Einstellung zum Schwäbischen.
- Hypothese: positive Einstellung schwächt den negativen Dialekteffekt ab.
- Zentrale Idee: Der Effekt hängt linear von der Haltung zum Dialekt ab.
Mittelwertzentrierung
Weil die Einstellungsvariable auf einer Skala von 1 bis 5 lag, wäre der Wert \(0\) ohne Zentrierung nicht sinnvoll interpretierbar. Deshalb wird die Variable mittelwertzentriert. Durch die Zentrierung wird \(0\) zum Mittelwert der Skala, sodass die Koeffizienten wieder sinnvoll als Effekte für durchschnittlich eingestellte Personen gelesen werden können.
- Zentrierung macht den Referenzwert \(0\) interpretierbar.
- Ohne Zentrierung wäre der Intercept schwer sinnvoll zu deuten.
- Für Moderationen mit metrischen Variablen ist das besonders wichtig.
Moderation durch Einstellung
Mit Interaktion zeigt sich: Die Einstellung zum Schwäbischen moderiert den Effekt des Dialekts signifikant. Je besser das Schwäbische bewertet wird, desto kleiner wird der negative Effekt des Dialekts. Bei sehr positiver Einstellung verschwindet der Unterschied zwischen Hochdeutsch und Schwäbisch fast ganz, bei negativer Einstellung wird er stark negativ.
- Interaktionseffekt ist signifikant und positiv.
- Der negative Dialekteffekt wird mit positiverer Einstellung schwächer.
- Mit jedem Punkt weniger auf der Skala verstärkt sich der negative Effekt deutlich.
Der zentrale Interaktionseffekt lässt sich hier so ausdrücken:
\[Y = b_0 + b_1X + b_2Z + b_3XZ\]
wobei \(X\) hier der Dialekt und \(Z\) die Einstellung zum Schwäbischen ist.
Grafische Deutung
Die Vorlesung zeigt zwei Arten, solche Effekte zu visualisieren: einmal über typische Moderatorwerte und einmal als kontinuierliche Funktion über alle Werte des Moderators. Beide Darstellungen machen deutlich, dass der Dialekteffekt bei niedriger Schwäbisch-Bewertung stark negativ ist, bei durchschnittlicher Bewertung noch negativ bleibt und bei hoher Bewertung nahezu verschwindet.
- Bei negativer Einstellung ist der Dialekteffekt am stärksten.
- Bei durchschnittlicher Einstellung bleibt ein kleiner negativer Effekt.
- Bei positiver Einstellung ist der Effekt fast weg.
Fazit
Lineare Modelle mit Moderation sind technisch einfach zu spezifizieren, aber ihre inhaltliche Interpretation ist deutlich anspruchsvoller als bei einfachen Regressionsmodellen. Die Vorlesung betont, dass man immer die Interaktion, die konditionalen Haupteffekte und passende Visualisierungen zusammen betrachten sollte.
- Technisch leicht, inhaltlich komplex.
- Interaktionen immer im Kontext des Moderators interpretieren.
- Nicht nur Signifikanz, sondern auch Richtung und Größe beachten.