2 Wiederholung: Univariate & bivariate Beschreibung von Daten
2.1 Folien
2.2 Daten der heutigen Sitzung
2.3 Code und Ausgaben aus der Vorlesung
Laden der relevanten Pakete
library(patchwork) # Mehrere Grafiken zusammen darstellen
library(report) # Einfaches Erstellen von statistischen Berichten
library(datawizard) # Für Kreuztabellen
library(tidyverse) # Datenmanagement und Visualisierung: https://www.tidyverse.org/── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.6
✔ forcats 1.0.1 ✔ stringr 1.6.0
✔ ggplot2 4.0.1 ✔ tibble 3.3.0
✔ lubridate 1.9.4 ✔ tidyr 1.3.1
✔ purrr 1.2.0
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsLesen und Aufbereiten des Datensatz von Van Erkel & Van Aelst
d <- haven::read_stata(here::here("data/Vanerkel_Vanaelst_2021.dta")) |>
rename(
Political_knowledge = PK,
Personalized_news = personalized_news,
Radio = News_channels_w4_1,
Television = News_channels_w4_2,
Newspapers = News_channels_w4_3,
Online_news_sites = News_channels_w4_4,
Twitter = News_channels_w4_5,
Facebook = News_channels_w4_6
) |>
mutate(
Gender = as_factor(Gender),
Education = as_factor(Education)
)Datensatz mit ausgewählten Variablen im Tabellenformat
d |>
select(
Age, Gender, Education,
Political_knowledge,
Online_news_sites,
Twitter,
Facebook
) |>
print(n = 30)# A tibble: 993 × 7
Age Gender Education Political_knowledge Online_news_sites Twitter Facebook
<dbl> <fct> <fct> <dbl> <dbl+lbl> <dbl+l> <dbl+lb>
1 45 female Middle 2 2 [Less than onc… 1 [Nev… 1 [Neve…
2 59 female High 4 5 [(Almost) dail… 1 [Nev… 1 [Neve…
3 52 female High 4 5 [(Almost) dail… 1 [Nev… 1 [Neve…
4 23 female High 1 5 [(Almost) dail… 4 [3 t… 6 [More…
5 23 female High 1 3 [1 to 2 times … 1 [Nev… 6 [More…
6 36 female Middle 2 3 [1 to 2 times … 1 [Nev… 1 [Neve…
7 21 female Middle 3 3 [1 to 2 times … 3 [1 t… 4 [3 to…
8 66 male Middle 3 2 [Less than onc… 1 [Nev… 1 [Neve…
9 68 male Middle 4 1 [Never] 1 [Nev… 1 [Neve…
10 70 female Middle 4 1 [Never] 1 [Nev… 1 [Neve…
11 65 female High 2 2 [Less than onc… 1 [Nev… 5 [(Alm…
12 28 female Middle 2 2 [Less than onc… 1 [Nev… 3 [1 to…
13 70 male High 4 6 [More than onc… 1 [Nev… 1 [Neve…
14 20 male Middle 0 4 [3 to 4 times … 1 [Nev… 3 [1 to…
15 50 female High 4 1 [Never] 1 [Nev… 1 [Neve…
16 32 female Middle 2 3 [1 to 2 times … 1 [Nev… 6 [More…
17 66 female Middle 3 2 [Less than onc… 1 [Nev… 3 [1 to…
18 63 female Middle 3 2 [Less than onc… 1 [Nev… 1 [Neve…
19 71 male High 5 6 [More than onc… 1 [Nev… 1 [Neve…
20 66 male Middle 4 1 [Never] 1 [Nev… 2 [Less…
21 24 male High 3 5 [(Almost) dail… 1 [Nev… 5 [(Alm…
22 36 female Middle 1 4 [3 to 4 times … 1 [Nev… 6 [More…
23 56 female High 4 5 [(Almost) dail… 1 [Nev… 1 [Neve…
24 22 male Middle 5 4 [3 to 4 times … 1 [Nev… 4 [3 to…
25 65 male Lower 5 1 [Never] 1 [Nev… 4 [3 to…
26 36 female High 4 6 [More than onc… 1 [Nev… 6 [More…
27 63 female Lower 1 1 [Never] 1 [Nev… 4 [3 to…
28 43 male High 3 5 [(Almost) dail… 3 [1 t… 3 [1 to…
29 42 male High 4 1 [Never] 1 [Nev… 1 [Neve…
30 43 female High 3 2 [Less than onc… 1 [Nev… 1 [Neve…
# ℹ 963 more rowsDatensatz mit ausgewählten Variablen in Variablenübersicht
d |>
select(
Age, Gender, Education,
Political_knowledge,
Information_overload,
Personalized_news,
Radio,
Television,
Newspapers,
Online_news_sites,
Twitter,
Facebook
) |>
glimpse()Rows: 993
Columns: 12
$ Age <dbl> 45, 59, 52, 23, 23, 36, 21, 66, 68, 70, 65, 28, 7…
$ Gender <fct> female, female, female, female, female, female, f…
$ Education <fct> Middle, High, High, High, High, Middle, Middle, M…
$ Political_knowledge <dbl> 2, 4, 4, 1, 1, 2, 3, 3, 4, 4, 2, 2, 4, 0, 4, 2, 3…
$ Information_overload <dbl+lbl> 11, 11, 7, 13, 5, 2, 5, 5, 4, 8, 5, …
$ Personalized_news <dbl+lbl> 5, NA, 5, 3, 3, 4, 6, NA, 8, NA, 3, …
$ Radio <dbl+lbl> 3, 5, 3, 2, 6, 3, 5, 6, 5, 1, 3, 1, 6, 3, 6, …
$ Television <dbl+lbl> 4, 3, 5, 5, 5, 1, 5, 5, 5, 5, 5, 1, 6, 4, 4, …
$ Newspapers <dbl+lbl> 2, 5, 1, 5, 3, 1, 2, 1, 5, 5, 5, 2, 6, 5, 6, …
$ Online_news_sites <dbl+lbl> 2, 5, 5, 5, 3, 3, 3, 2, 1, 1, 2, 2, 6, 4, 1, …
$ Twitter <dbl+lbl> 1, 1, 1, 4, 1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, …
$ Facebook <dbl+lbl> 1, 1, 1, 6, 6, 1, 4, 1, 1, 1, 5, 3, 1, 3, 1, …Soziodemographie der Stichprobe als Tabelle
d |>
select(Gender, Education, Age) |>
report_sample()# Descriptive Statistics
Variable | Summary
-------------------------------------
Gender [female], % | 47.7
Education [Lower], % | 13.7
Education [Middle], % | 40.7
Education [High], % | 45.6
Mean Age (SD) | 52.98 (13.96)Soziodemographie der Stichprobe als Text
d |>
select(Gender, Education, Age) |>
report_text()The data contains 993 observations of the following 3 variables:
- Gender: 2 levels, namely male (n = 519, 52.27%) and female (n = 474, 47.73%)
- Education: 3 levels, namely Lower (n = 136, 13.70%), Middle (n = 404, 40.68%) and High (n = 453, 45.62%)
- Age: n = 993, Mean = 52.98, SD = 13.96, Median = 56.00, MAD = 14.83, range: [19, 71], Skewness = -0.70, Kurtosis = -0.54, 0% missing
Soziodemographie der Stichprobe als Abbildungen
theme_set(theme_minimal(base_size = 12)) # Formatvorlage für Abbildungen setzen
# Drei Abbildungen erstellen
p1 <- d |>
ggplot(aes(Gender)) +
geom_bar()
p2 <- d |>
ggplot(aes(Education)) +
geom_bar()
M_age <- mean(d$Age) # Für Markierung des Mittelwerts
Mdn_age <- median(d$Age) # Für Markierung des Median
p3 <- d |>
ggplot(aes(Age)) +
geom_histogram(binwidth = 5) +
geom_vline(xintercept = M_age, color = "red", linewidth = 2) +
geom_vline(xintercept = Mdn_age, color = "green", linewidth = 2)
# Drei Abbildungen gemeinsam darstellen
p1 + p2 + p3 + plot_layout(widths = c(1, 2, 3))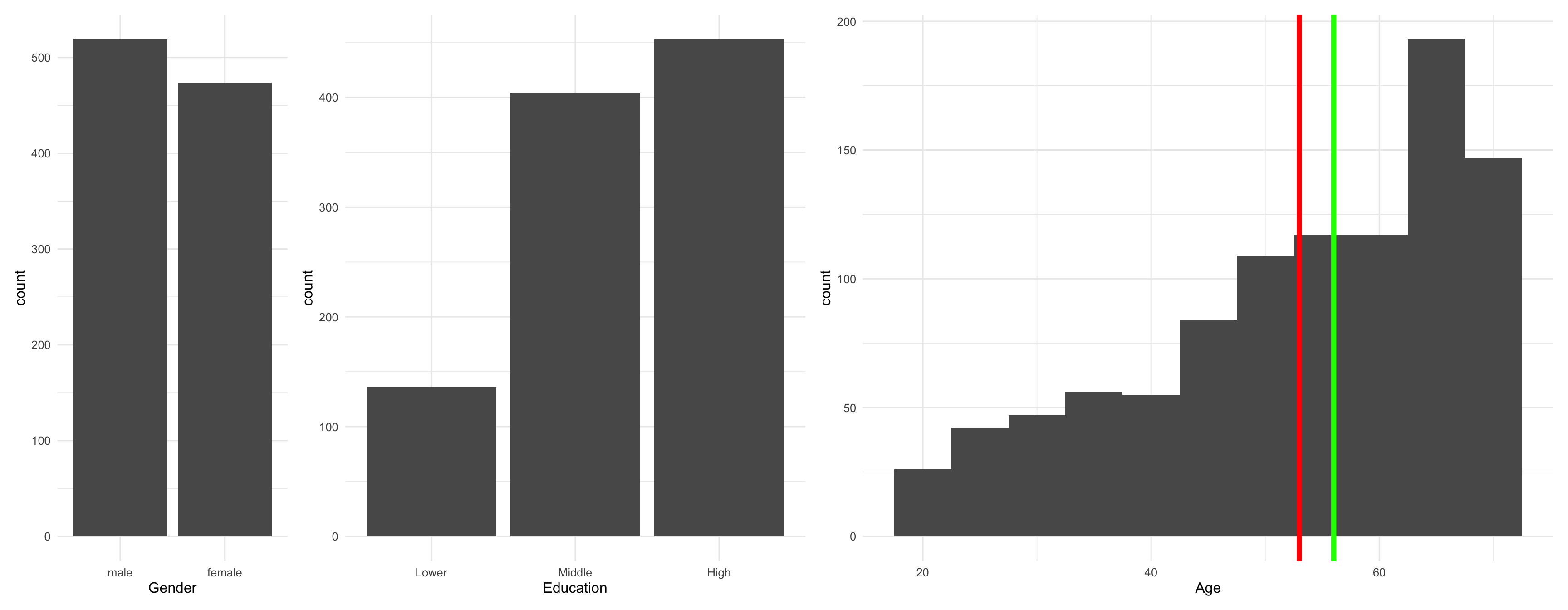
Tabelle 2 aus dem Artikel replizieren
d |>
select(
Political_knowledge,
Information_overload,
Personalized_news,
Radio,
Television,
Newspapers,
Online_news_sites,
Twitter,
Facebook
) |>
haven::zap_labels() |> # Entfernt labels, da das {report} Paket damit nicht umgehen kann
report_sample()# Descriptive Statistics
Variable | Summary
--------------------------------------------
Mean Political_knowledge (SD) | 3.04 (1.36)
Mean Information_overload (SD) | 8.46 (3.16)
Mean Personalized_news (SD) | 5.16 (1.92)
Mean Radio (SD) | 3.81 (1.73)
Mean Television (SD) | 4.43 (1.33)
Mean Newspapers (SD) | 3.52 (1.69)
Mean Online_news_sites (SD) | 3.44 (1.72)
Mean Twitter (SD) | 1.34 (0.99)
Mean Facebook (SD) | 2.69 (1.95)Tabelle 2 aus dem Artikel erweitern
d |>
select(
Political_knowledge,
Information_overload,
Personalized_news,
Radio,
Television,
Newspapers,
Online_news_sites,
Twitter,
Facebook
) |>
haven::zap_labels() |>
report::report() |>
as.data.frame()Variable | n_Obs | Mean | SD | Median | MAD | Min | Max
----------------------------------------------------------------------
Political_knowledge | 993 | 3.04 | 1.36 | 3 | 1.48 | 0 | 5
Information_overload | 993 | 8.46 | 3.16 | 8 | 2.97 | 0 | 16
Personalized_news | 993 | 5.16 | 1.92 | 5 | 1.48 | 0 | 12
Radio | 993 | 3.81 | 1.73 | 4 | 1.48 | 1 | 6
Television | 993 | 4.43 | 1.33 | 5 | 0.00 | 1 | 6
Newspapers | 993 | 3.52 | 1.69 | 4 | 1.48 | 1 | 6
Online_news_sites | 993 | 3.44 | 1.72 | 4 | 1.48 | 1 | 6
Twitter | 993 | 1.34 | 0.99 | 1 | 0.00 | 1 | 6
Facebook | 993 | 2.69 | 1.95 | 2 | 1.48 | 1 | 6
Variable | Skewness | Kurtosis | percentage_Missing
---------------------------------------------------------------
Political_knowledge | -0.40 | -0.47 | 0.00
Information_overload | -0.22 | 0.09 | 0.00
Personalized_news | -0.02 | 0.35 | 21.55
Radio | -0.41 | -1.22 | 0.00
Television | -1.23 | 0.73 | 0.00
Newspapers | -0.25 | -1.34 | 0.00
Online_news_sites | -0.15 | -1.37 | 0.00
Twitter | 3.24 | 10.04 | 0.00
Facebook | 0.57 | -1.35 | 0.00Tabelle 3 aus dem Artikel replizieren
tab3 <- d |>
select(
Radio,
Television,
Newspapers,
Online_news_sites,
Twitter,
Facebook
) |>
mutate(
across(everything(), as_factor)
) |>
haven::zap_labels() |>
report_sample() |>
# Ab hier nur Formatierung, um Tabelle aus Artikel genau nachzubauen.
separate(Variable, c("Variable", "Class"), sep = " \\[") |>
spread(Variable, Summary) |>
mutate(Class = str_remove_all(Class, fixed("],"))) |>
_[c(6, 4, 2, 3, 1, 5), c(1, 5, 6, 3, 4, 7, 2)]
tab3 Class Radio Television Newspapers Online_news_sites Twitter
6 Never % 16.3 6.1 19.6 21.9 85.3
4 Less than once a week % 11.4 5.0 12.6 12.5 6.2
2 1 to 2 times a week % 12.4 10.3 13.8 13.4 2.7
3 3 to 4 times a week % 11.2 10.5 12.9 15.1 1.8
1 (Almost) daily % 32.5 54.2 32.6 26.9 2.5
5 More than once a day % 16.2 13.9 8.5 10.3 1.4
Facebook
6 49.5
4 8.1
2 7.2
3 6.8
1 16.1
5 12.3tab3 |>
mutate(across(2:7, cumsum)) Class Radio Television Newspapers Online_news_sites Twitter
6 Never % 16.3 6.1 19.6 21.9 85.3
4 Less than once a week % 27.7 11.1 32.2 34.4 91.5
2 1 to 2 times a week % 40.1 21.4 46.0 47.8 94.2
3 3 to 4 times a week % 51.3 31.9 58.9 62.9 96.0
1 (Almost) daily % 83.8 86.1 91.5 89.8 98.5
5 More than once a day % 100.0 100.0 100.0 100.1 99.9
Facebook
6 49.5
4 57.6
2 64.8
3 71.6
1 87.7
5 100.0Abbildung 1 aus dem Artikel replizieren
d |>
ggplot(aes(Political_knowledge)) +
geom_bar()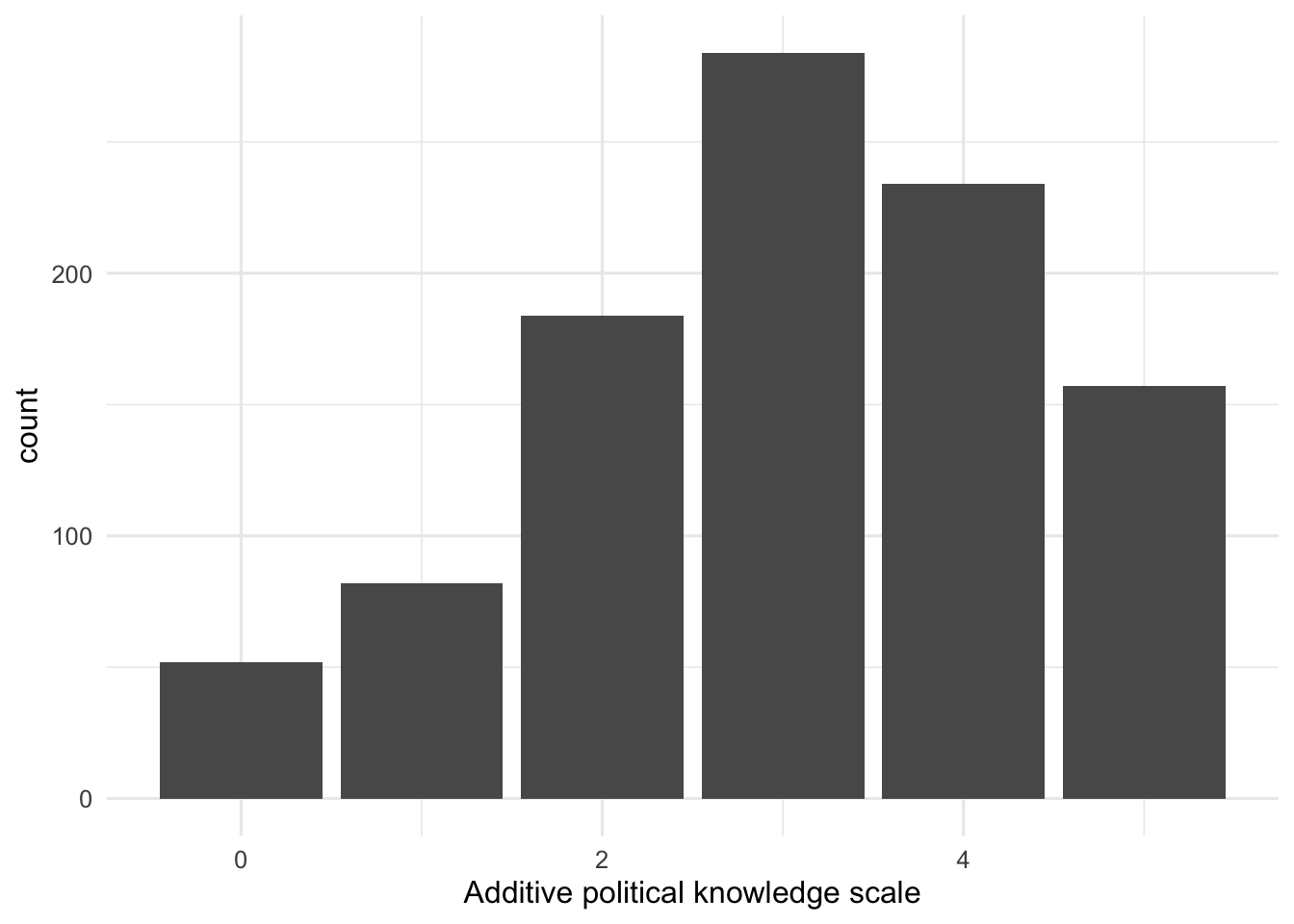
Begleitender Text zu Abbildung 1
d$Political_knowledge |>
report_text()d$Political_knowledge: n = 993, Mean = 3.04, SD = 1.36, Median = 3.00, MAD = 1.48, range: [0, 5], Skewness = -0.40, Kurtosis = -0.47, 0% missing
Kreuztabelle
d |>
mutate(trad = factor(trad, labels = c(
"traditional news diet: no",
"traditional news diet: yes"
))) |>
data_tabulate(
select = trad, by = "Gender",
remove_na = TRUE, proportions = "column"
)Gruppenanteile als Abbildung I
d |>
mutate(trad = factor(trad, labels = c(
"trad. news: no",
"trad. news: yes"
))) |>
ggplot(aes(trad, fill = Gender)) +
geom_bar(
aes(y = after_stat(count / tapply(count, fill, sum)[fill])),
position = position_dodge()
) +
scale_y_continuous(name = NULL, labels = scales::percent_format(accuracy = 1))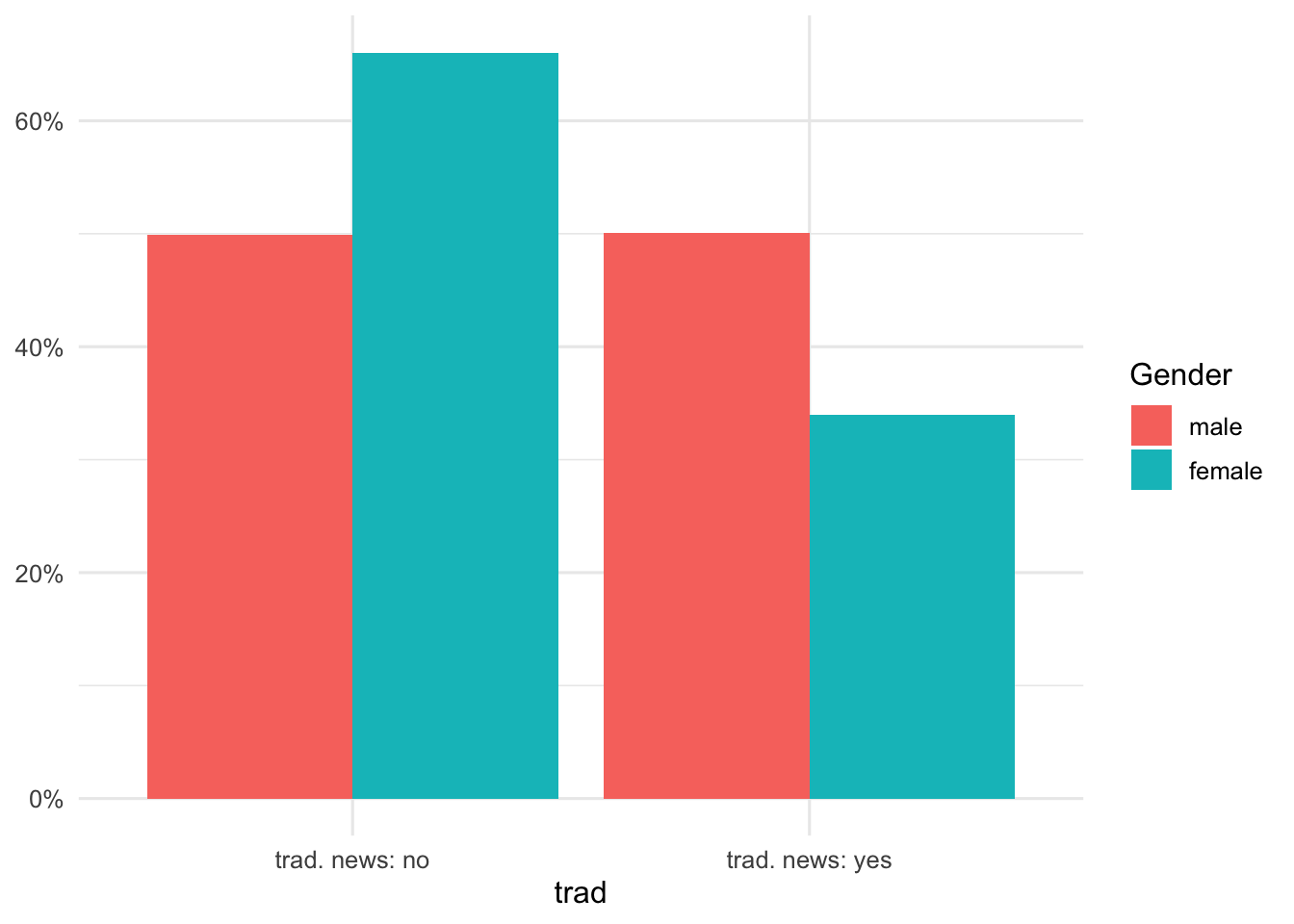
Gruppenanteile als Abbildung II
d |>
mutate(trad = factor(trad, labels = c(
"no",
"yes"
))) |>
ggplot(aes(trad, fill = Gender)) +
geom_bar(
aes(y = after_stat(count / tapply(count, fill, sum)[fill])),
position = position_dodge()
) +
scale_y_continuous(name = NULL, labels = scales::percent_format(accuracy = 1)) +
facet_wrap("Gender")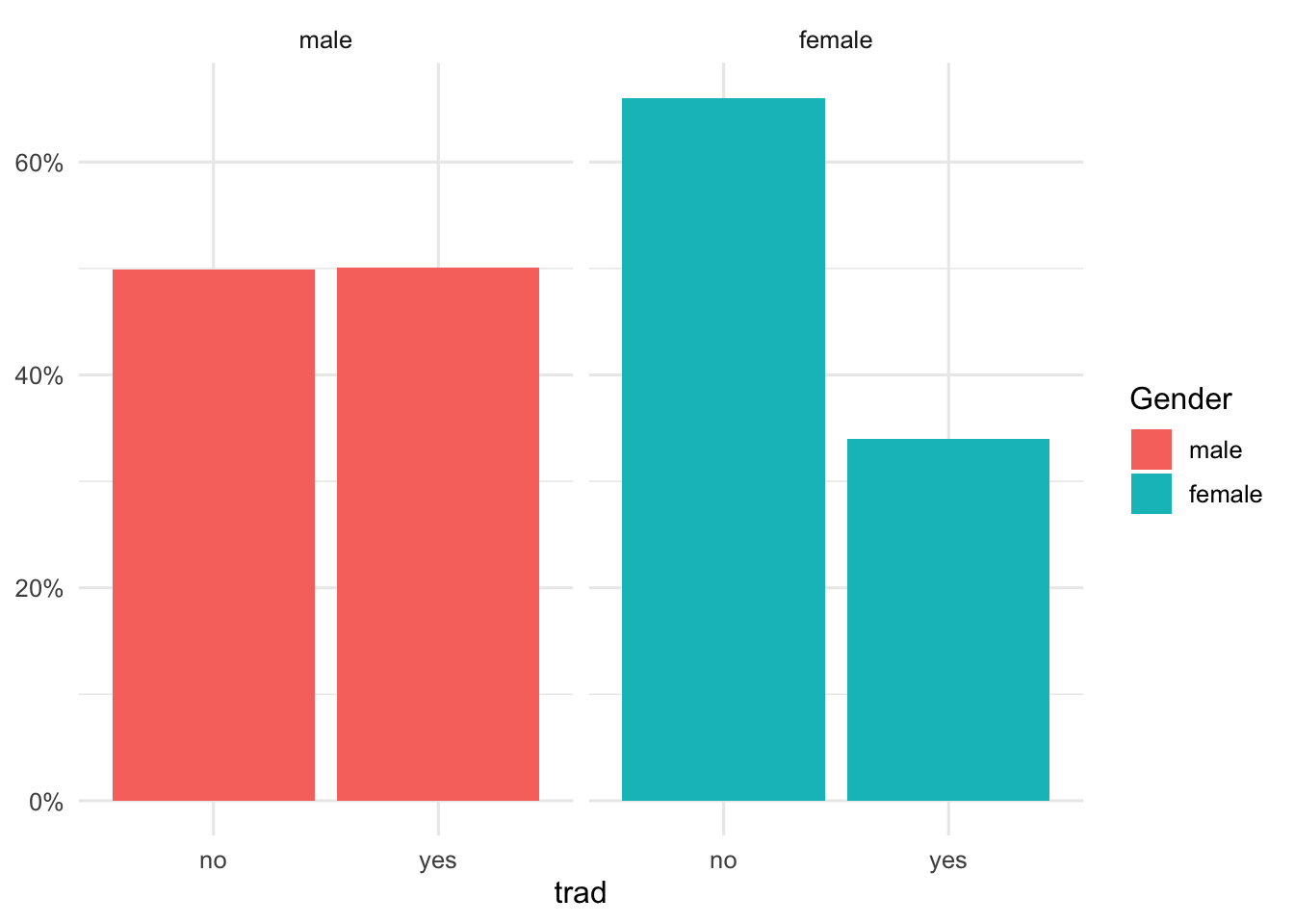
Kennwerte für Gruppen (M, SD)
d |>
select(Political_knowledge, Gender) |>
report_sample(by = "Gender")# Descriptive Statistics
Variable | male (n=519) | female (n=474) | Total (n=993)
-----------------------------------------------------------------------------
Mean Political_knowledge (SD) | 3.44 (1.32) | 2.61 (1.28) | 3.04 (1.36)Kennwerte für Gruppen (mehr Kennwerte) mit summarise() aus dem {tidyverse}
d |>
select(Political_knowledge, Gender) |>
summarise(
n = n(),
M = mean(Political_knowledge),
SD = sd(Political_knowledge),
Mdn = median(Political_knowledge),
MAD = mad(Political_knowledge),
Min = min(Political_knowledge),
Max = max(Political_knowledge),
Skewness = e1071::skewness(Political_knowledge), # Paket e1071 muss ggf. installiert werden
Kurtosis = e1071::kurtosis(Political_knowledge), # Paket e1071 muss ggf. installiert werden
.by = Gender
)# A tibble: 2 × 10
Gender n M SD Mdn MAD Min Max Skewness Kurtosis
<fct> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 female 474 2.61 1.28 3 1.48 0 5 -0.207 -0.443
2 male 519 3.44 1.32 4 1.48 0 5 -0.720 -0.02422.4 Hausaufgabe
Vollziehen Sie die Analysen nach, deren Ausgaben wir in der Vorlesung besprochen haben.
- Vergleichen Sie Ihre Ausgaben mit den Ausgaben und, falls zutreffend, mit den relevanten Stellen in Van Erkel & Van Aelst (2021).
- Interpretieren Sie alle Ausgaben und stellen Sie sicher, dass Sie die Bedeutung jeder Zahl verstehen.
- Notieren Sie alle Zahlen, die Sie nicht verstanden haben, und fragen Sie nach.
Lösung
2.5 Transkript Teil 1 (Vorlesungssitzung 2)
Das folgende Transkript wurde auf Basis der Aufzeichnung der Vorlesung erstellt. Die vollständige Aufzeichnungen inklusive der Bildschirminhalte sind in Blackboard🔒 verfügbar. Die Tonspur wurde mit VoiceAI transkribiert. Das Transkript wurde dann mit Sprachmodellen (v.a. Claude Sonnet 4.5) geglättet und formatiert. In diesem Prozess kann es an verschiedenen Stellen zu Fehlern kommen. Im Zweifel gilt das gesprochene Wort, und auch beim Vortrag mache ich Fehler.
Ich stelle das Transkript hier als experimentelles, ergänzendes Material zur Dokumentation der Vorlesung zur Verfügung. Noch bin ich mir unsicher, ob es eine sinnvolle Ergänzung ist und behalte mir vor, es weiter zu bearbeiten oder zu löschen.
Organisatorisches
Die Aufzeichnung der ersten Vorlesung wurde erfolgreich erstellt und ist verhältnismäßig verständlich. Es wird voraussichtlich Aufzeichnungen der Sitzungen geben, allerdings ohne Garantie, da die Technik nicht vollständig kontrollierbar ist. Die Videos werden in den kommenden Wochen im Blackboard zur Verfügung gestellt, nachdem geprüft wurde, ob eine Bearbeitung notwendig ist.
Die Aufzeichnung läuft über das Mikrofon am Pult. Fragen ohne Mikrofon werden nicht aufgezeichnet. Wer möchte, dass die eigene Frage in der Aufzeichnung enthalten ist, kann nach einem Mikrofon fragen.
Überblick zur heutigen Sitzung
Die heutige Sitzung beschäftigt sich mit der Wiederholung der univariaten und bivariaten beschreibenden Statistik. Es gibt sehr viele Folien, die nicht alle besprochen werden. Ein Teil davon dient zum Nachschlagen. Die Sitzung zeigt auch einen ersten Einstieg in RStudio und R, zunächst durch das Lesen von R-Code, um einen ersten Eindruck zu vermitteln, wie das funktioniert. Es geht vor allem darum, solche Analysen im Grundsatz zu verstehen. Bei späteren Sitzungen mit neuen und komplexeren statistischen Verfahren wird das Material weniger dicht sein.
Vorkenntnisse der Teilnehmenden
An der Befragung haben 76 Personen teilgenommen. Über 80 Prozent haben bereits mindestens eine Statistikvorlesung besucht und sollten von den heute verwendeten Begriffen schon gehört haben. Bei qualitativen Analysemethoden sind die Vorkenntnisse aus Vorlesungen etwas geringer. Praktische Erfahrungen zeigen ein ausgeglicheneres Bild: Knapp mehr als die Hälfte hat bereits quantitative Arbeiten durchgeführt, noch etwas mehr haben qualitative Arbeiten selbst gemacht.
Circa die Hälfte bis ein Viertel traut sich die Durchführung qualitativer Verfahren selbst zu. Bei quantitativen Analyseverfahren und Statistik zeigt sich ein Gap zwischen dem, was interpretiert werden könnte, und dem, was selbst durchgeführt werden könnte. Circa die Hälfte traut sich die Arbeit mit Standardverfahren zu, was ein guter Ausgangspunkt ist. Für die andere Hälfte besteht subjektiv Nachholbedarf.
Bei der Software-Vorerfahrung hat die Mehrheit noch keine Erfahrung mit Datenanalysesoftware. Excel ist das am häufigsten genutzte Tool. Bei quantitativer Software halten sich SPSS und RStudio etwa die Waage mit jeweils etwa einem Drittel Nutzungserfahrung. MaxQDA wurde von etwa einem Drittel für qualitative Arbeiten verwendet.
Beschreibende Statistik: Grundlagen
Beschreibende oder deskriptive Statistik bedeutet, viele Zahlen – die erhobenen Daten – durch weniger Zahlen zu beschreiben, um Ergebnisse selbst gut verstehen und kommunizieren zu können. Dazu werden Grafiken, Tabellen und Kennwerte erstellt. Die beschreibende Statistik beschreibt nur die Stichprobe, also die Fälle im Datensatz. Sie sagt noch nichts über Grundgesamtheiten aus, aus der die Stichprobe kommt. Das ist Aufgabe der Inferenzstatistik, die in der nächsten Woche wiederholt wird.
Skalenniveaus
Das Skalenniveau ist eine der zentralen Grundlagen. Es wird unterschieden zwischen:
Nominalskala: Variablen wie Gender, bei denen für jede Ausprägung nur festgestellt werden kann, ob ein Fall diese Ausprägung hat oder nicht. Es gibt keine Rangordnung. Bei der Analyse wird gezählt, wie häufig verschiedene Ausprägungen vorkommen.
Metrische Skalen (Ordinal-, Intervall-, Verhältnisskala): Variablen, bei denen Rangordnungen gefunden werden können und mit denen gerechnet werden kann. Beispielsweise politisches Wissen mit fünf Wissensfragen, bei denen die Anzahl richtig beantworteter Fragen gezählt wird. Hier werden Durchschnitt, Median und ähnliche Kennwerte berechnet.
Das Skalenniveau bestimmt, welche statistischen Maßzahlen sinnvoll angewendet werden können. Wer sich unsicher fühlt, sollte dies nachlesen, beispielsweise bei Brosius et al.
Häufigkeitsanalysen
Bei Häufigkeitsanalysen werden alle Ausprägungen einer Variable genommen und gezählt, wie häufig sie vorkommen. Die Darstellung erfolgt durch absolute Zahlen oder Anteile, entweder in Tabellen, einzelnen Zahlen oder grafisch. Dies ist die einfachste Form, Daten zusammenzufassen.
Kennwerte zur Beschreibung
Kennwerte dienen dazu, mit wenigen Werten die Daten möglichst gut zu beschreiben. Die Zahlen sollen Informationen reduzieren und komprimieren. Sie sollen empfindlich gegenüber Veränderungen sein (genau), aber auch robust (ein Ausreißer sollte die Maßzahl nicht völlig verändern).
Kennwerte der zentralen Tendenz beschreiben einen einzelnen, sehr typischen Wert für die Verteilung:
- Arithmetisches Mittel (Durchschnitt)
- Median (mittlerer Fall)
- Modus (häufigster Wert)
Maßzahlen der Streuung geben an, wie typisch der zentrale Wert wirklich ist:
- Standardabweichung (fast immer berichtet)
- Bei kleiner Streuung ist der zentrale Wert sehr typisch
- Bei großer Streuung sind die Fälle weit um den zentralen Wert verteilt
Immer wenn ein arithmetisches Mittel berichtet wird, sollte auch die Standardabweichung berichtet werden, um zu zeigen, wie typisch dieser Wert ist.
Weitere Maßzahlen:
- Schiefe: Liegt der Schwerpunkt der Verteilung eher links oder rechts?
- Wölbung (Kurtosis): Läuft die Verteilung spitz zu oder ist sie breit?
Diese werden in der Praxis seltener berichtet. Linksschiefe Verteilungen steigen leicht an und fallen stärker ab. Rechtsschiefe Verteilungen verlaufen umgekehrt.
Es müssen keine Formeln auswendig gelernt werden. Es geht darum, mit den Analysen inhaltlich arbeiten zu können.
Datensatz Van Erkel & Van Aelst
Die Studie untersucht, warum und wann Mediennutzung zu Wissenszuwachs führt. Es geht um Surveillance Knowledge – beobachtendes Wissen darüber, was gerade politisch passiert. Vor Social Media war die Idee, dass Massenmedien wie die Tagesschau allen ein solches Grundwissen zur Verfügung stellen.
Mit fragmentierter Medienlandschaft und Social Media stellt sich die Frage, ob dies noch funktioniert. Einige Studien zeigen, dass Menschen mit hoher Social Media-Nutzung ein hohes gefühltes Wissen haben, aber bei Wissenstests nicht besser abschneiden – eine “Illusion of Knowledge”.
Van Erkel und Van Aelst führten eine Studie in Flandern durch mit 993 Befragten. Es wurden fünf Wissensfragen gestellt (richtige und falsche Antworten möglich) und nach der Mediennutzung gefragt. Die Forschenden haben ihre Daten und ihren Analysecode veröffentlicht, sodass die Analyse nachvollzogen werden kann.
Datenstruktur
Ein Datensatz ist eine Tabelle mit Variablen in den Spalten (die gestellten Fragen) und Fällen in den Zeilen (die befragten Personen). Für politisches Wissen gibt es Werte von 0 bis 5 (Anzahl richtig beantworteter Fragen). Bei Mediennutzung wurden Häufigkeiten erfragt auf Skalen, die meist von 1 (never) bis 6 (mehrmals täglich) reichen.
Wichtig: Bei politischem Wissen beginnt die Skala bei 0 (0 Fragen richtig), während Mediennutzungsskalen bei 1 beginnen (never). Dies ist eine definierte Entscheidung, die bestimmt, wie später mit den Werten gerechnet werden kann. Ein Mittelwert von 1,3 ist nahe bei “never”, während ein Mittelwert kleiner als 1 gar nicht möglich ist.
Soziodemografische Beschreibung
Für kategoriale Variablen (nominal oder ordinal) werden Anteile angegeben:
- Gender: 47,7% identifizierten sich als weiblich
- Bildung: Relativ geringe Zahl gering gebildeter Menschen, jeweils knapp die Hälfte mittel- und hochgebildet – eine verhältnismäßig hochgebildete Stichprobe
Für metrische Variablen werden Mittelwert und Standardabweichung berichtet:
- Alter: Durchschnitt 53 Jahre, Standardabweichung 14 Jahre
- Die 53 Jahre sind nicht besonders typisch, da die Streuung sehr groß ist
- In der grafischen Darstellung (Histogramm) zeigt sich, dass bei jüngeren Menschen weniger Befragte vorliegen, bei älteren mehr
- Die Schiefe ist negativ (linksschief), die Kurtosis ist negativ (relativ breite Verteilung)
Politisches Wissen und weitere Variablen
Politisches Wissen: Im Durchschnitt und im Median wurden drei von fünf Fragen richtig beantwortet. Die Standardabweichung liegt bei 1,4 Punkten. Das bedeutet, es wäre eine starke Verkürzung zu sagen, die Menschen beantworten drei Fragen richtig. Werte zwischen etwa zwei und vier Fragen richtig sind verhältnismäßig typisch für diese Verteilung. Alle fünf Fragen richtig zu haben oder keine bzw. nur eine richtig zu haben, ist eher untypisch.
Information Overload Index (0 bis 16): Mehrere Indikatoren wurden zu einem Index zusammengefasst. 0 bedeutet kein gefühlter Information Overload, 16 bedeutet komplett von Informationen überlastet. Bei diesem Index wurden alle Fragen so gestellt, dass hohe Antworten auf hohen Overload hindeuten.
Personalized News Environment Index (0 bis 12): Ebenfalls aus mehreren Fragen zusammengesetzt. 0 bedeutet, Nachrichten sind gar nicht personalisiert, 12 bedeutet, Nachrichten sind genau zugeschnitten. Hier wurden Fragen in beide Richtungen gestellt. Bevor der Index berechnet wird, müssen Fragen, bei denen hohe Antworten niedriges Personalized News Environment implizieren, umgedreht werden. Das Mischen der Fragerichtungen soll helfen, dass Befragte die Fragen tatsächlich lesen und durchdenken, statt einfach durchzukreuzen.
Mediennutzung
Die Befragten wurden nach ihrer Nutzung von Nachrichten in verschiedenen Kanälen gefragt: Radio, Fernsehen, Zeitungen, Online-Nachrichten, Twitter und Facebook. Die Skala reichte von 1 (never) bis 6 (mehrmals täglich).
Klassische Medien werden in dieser Stichprobe am häufigsten genutzt. Facebook als Social Media-Kanal wird im Mittel seltener genutzt als Zeitung oder Radio, hat aber eine große Streuung. Dies könnte auf unterschiedliches Nutzungsverhalten verschiedener Altersgruppen hindeuten – eine Hypothese für bivariate Analyse.
Bei den Standardabweichungen fällt auf, dass die Streuung nur in Relation zur Skala sinnvoll interpretierbar ist. Die Medienskalen (1-6) und die Wissensskala (0-5) sind zwar ähnlich breit, messen aber völlig unterschiedliche Dinge. Daher ist ein direkter Vergleich der Standardabweichungen nicht sinnvoll.
Die MAD-Werte (Median Absolute Deviation) zeigen häufig ähnliche Werte (1,48 oder 0,0). Dies liegt an der Berechnungsweise: Die mittlere absolute Abweichung vom Median wird mit 1,48 multipliziert, um sie mit der Standardabweichung vergleichbar zu machen. Diese Normierung bezieht sich auf die Standard-Normalverteilung.
Einführung in R und RStudio
R ist eine Programmiersprache zur Arbeit mit Daten. Es gibt ein Basispaket und viele Erweiterungspakete (Libraries). Am Anfang jeder R-Session müssen die benötigten Libraries geladen werden, zum Beispiel mit library().
Grundlegende Schritte einer Analyse:
- Pakete laden: Mit Befehlen wie
library(tidyverse)werden Werkzeuge geladen, die für die Analyse benötigt werden. Warnungen können meist ignoriert werden, solange alles funktioniert. - Daten einlesen: Mit Funktionen wie
haven::read_stata()werden Daten eingelesen. Das Assignment<-weist die gelesenen Daten einem Objekt zu, z.B.d <- haven::read_stata("pfad/datei.dta"). - Daten aufbereiten: Mit der Pipe
|>werden weitere Schritte angehängt:rename(): Variablen umbenennen (z.B.pol_knowledge = PK)mutate(): Variablen umwandeln (z.B. in Faktoren für kategoriale Variablen)
- Analysen durchführen: Wieder mit Pipe-Struktur:
select(): Variablen auswählenreport_sample(): Deskriptive Statistiken erstellen- Die Ausgabe wird mit
print()angezeigt
R-Code lesen lernen: Es geht jetzt noch nicht darum, Code selbst schreiben zu können, sondern ihn zu verstehen. Die Logik ist sequentiell von oben nach unten. Man beginnt mit einem Datensatz, wendet dann Funktionen an (durch Pipes verbunden), um Variablen auszuwählen, zu transformieren oder zu analysieren.
Beispiel: d |> select(gender, education, age) |> report_sample() bedeutet: Nimm den Datensatz d, wähle die Variablen gender, education und age aus, und erstelle dann eine deskriptive Statistik.
Hilfsmittel
Large Language Models oder KI-Assistenten können sehr gut helfen, R-Code zu verstehen. Man kann z.B. Chat-AI (mit Uni-Account kostenlos) oder KI-Assist-at-FU nutzen und eingeben: “Erkläre mir den folgenden R-Code Schritt für Schritt”. Die Erklärungen können sehr hilfreich sein.
Auch Analyseoutputs können an solche Assistenten übergeben werden mit der Bitte: “Das ist die Ausgabe meiner Analyse, hilf mir, einen kurzen Absatz dazu zu schreiben.”
Übungsaufgaben
Die univariaten beschreibenden Analysen sollten nachvollzogen werden, entweder durch eigene Reproduktion in R/RStudio oder durch Durcharbeiten des kompilierten Materials auf der Webseite. Wichtig ist das Verständnis der Statistiken als Grundlage für weitergehende Verfahren in kommenden Sitzungen.
Bei allen Ausgaben sollte klar sein, was jede Zahl inhaltlich bedeutet. Es muss nicht bekannt sein, wie die Berechnung mit dem Taschenrechner funktioniert. Aber es muss verstanden werden, was beispielsweise ein Mittelwert von 3 mit Standardabweichung 1,3 für die Verteilung bedeutet.
2.6 Transkript Teil 2 (Vorlesungssitzung 3)
Das folgende Transkript wurde auf Basis der Aufzeichnung der Vorlesung erstellt. Die vollständige Aufzeichnungen inklusive der Bildschirminhalte sind in Blackboard🔒 verfügbar. Die Tonspur wurde mit VoiceAI transkribiert. Das Transkript wurde dann mit Sprachmodellen (v.a. Claude Sonnet 4.5) geglättet und formatiert. In diesem Prozess kann es an verschiedenen Stellen zu Fehlern kommen. Im Zweifel gilt das gesprochene Wort, und auch beim Vortrag mache ich Fehler.
Ich stelle das Transkript hier als experimentelles, ergänzendes Material zur Dokumentation der Vorlesung zur Verfügung. Noch bin ich mir unsicher, ob es eine sinnvolle Ergänzung ist und behalte mir vor, es weiter zu bearbeiten oder zu löschen.
Bivariate Beschreibung
In diesem Teil der Vorlesung geht es darum, wie zwei Variablen gemeinsam beschrieben werden können. Dabei interessiert uns, wie sich die Verteilung einer Variablen verändert, wenn wir sie nach den Ausprägungen einer anderen Variable betrachten, oder wie ihre gemeinsame Verteilung insgesamt aussieht. Die Analyse bleibt dabei vollständig deskriptiv: Alle Aussagen beziehen sich ausschließlich auf die beobachtete Stichprobe, nicht auf die Grundgesamtheit.
Wichtige Begriffe
Bivariate Datenanalyse
Unter bivariater Datenanalyse versteht man die Beschreibung der Verteilung einer Variable in Abhängigkeit von einer anderen oder die Darstellung der gemeinsamen Verteilung beider Variablen.
Abhängige und unabhängige Variable
Die abhängige Variable ist die Variable, deren Verteilung erklärt oder beschrieben werden soll, etwa politisches Wissen. Die unabhängige Variable dient als erklärende Variable; nach ihren Ausprägungen wird gruppiert, beispielsweise nach Gender oder der Nutzung traditioneller Medien.
Kreuztabellen: Beispiel traditionelle Mediennutzung × Gender
Eine wichtige Technik der bivariaten Beschreibung bei zwei kategorialen Variablen ist die Kreuztabelle. Sie zeigt übersichtlich, wie häufig bestimmte Kombinationen von Kategorien auftreten. In der Interpretation arbeitet man meist nicht mit absoluten Häufigkeiten, sondern mit Prozenten, weil diese den Vergleich verschieden großer Gruppen erleichtern.
Im Beispiel von Van Erkel & Van Aelst wird untersucht, wie verbreitet eine „traditional news diet“ bei Männern und Frauen ist. Diese Variable fasst Personen zusammen, die Facebook höchstens ein- bis zweimal pro Woche oder seltener nutzen, aber gleichzeitig traditionelle Nachrichtenquellen wie Fernsehen, Radio oder Zeitungen konsumieren. In der Kreuztabelle steht die gruppenbildende Variable (Gender) in den Spalten, und die Spaltenprozente geben an, wie groß der Anteil an Personen mit traditionellem Medienrepertoire innerhalb jeder Geschlechtsgruppe ist.
Bei der Interpretation achtet man zuerst auf die Spaltenprozente. Da sich die Gruppengrößen von Männern und Frauen unterscheiden, sind prozentuale Anteile innerhalb der Gruppen aussagekräftiger als absolute Werte. In der betrachteten Stichprobe verfügt etwa die Hälfte der befragten Männer, aber nur etwa ein Drittel der befragten Frauen über ein traditionelles Medienrepertoire. Damit ist es bei Männern klar verbreiteter. Wichtig ist dabei eine präzise Formulierung: Die Aussage bezieht sich ausschließlich auf Anteile und sagt nichts über die Intensität oder Vielfalt der Mediennutzung innerhalb der Gruppen aus.
Grafische Darstellung von Gruppenanteilen
Die Informationen aus einer einfachen Vier-Felder-Kreuztabelle (beispielsweise „traditionelles Medienrepertoire: ja/nein × Gender: männlich/weiblich“) können alternativ auch grafisch dargestellt werden.
Typische Grafiken sind gestapelte Balkendiagramme, in denen innerhalb jeder Geschlechtsgruppe die Anteile der Personen mit und ohne traditionelles Medienrepertoire aufgeführt werden, oder gruppierte Balkendiagramme, die innerhalb der Gruppen die Verteilung der Ausprägungen einer Variable darstellen. Solche Grafiken erleichtern das schnelle Erfassen von Unterschieden, sind aber bei wenigen Kategorien nicht zwingend notwendig, wenn die Kreuztabelle übersichtlich ist.
Kennwerte nach Gruppen: Mittelwerte und Streuungen
Wenn die abhängige Variable metrisch ist, wie etwa politisches Wissen (Zahl der richtig beantworteten Fragen von 0 bis 5), können bivariate Beschreibungen auch über Kennwerte wie Mittelwerte und Streuungen erfolgen. Die unabhängige Variable ist in diesem Fall üblicherweise kategorial (z. B. Gender). Für jede Gruppe werden dann ein Mittelwert und eine Standardabweichung berechnet.
Im Beispiel zu politischem Wissen und Gender basiert das Wissen auf fünf Wissensfragen, die 0 bis 5 richtige Antworten ermöglichen. Der Mittelwert gibt an, wie viele Fragen eine Person durchschnittlich richtig beantwortet. Die Standardabweichung zeigt, wie stark sich die Personen innerhalb einer Gruppe unterscheiden; sie kann als typische Abweichung vom Gruppenmittelwert gelesen werden.
Im Datensatz ergibt sich, dass Männer im Durchschnitt mehr politische Wissensfragen korrekt beantworten als Frauen, während die Streuung in beiden Gruppen ähnlich groß ist. Um die Größe des Unterschieds besser einordnen zu können, wird zusätzlich Cohen’s d berechnet, also die Differenz der Mittelwerte geteilt durch die Standardabweichung. Ein Wert von etwa 0,6 Standardabweichungen wird hier als spürbar, aber nicht extrem eingestuft.
R und RStudio in der Vorlesung
R und RStudio werden genutzt, um die statistischen Verfahren der Vorlesung praktisch nachzuvollziehen. Das Ziel ist nicht, dass alle Studierenden direkt flüssig programmieren, sondern dass sie verstehen, wie Tabellen, Kennwerte und Grafiken mithilfe von Code entstehen.
RStudio-Projekte und Dateistruktur
Es wird empfohlen, mit RStudio-Projekten zu arbeiten, da damit klar festgelegt ist, in welchem Ordner Daten, Skripte und Ergebnisse gespeichert sind. Ein Projekt entspricht einem Ordner, der eine Projektdatei enthält; beim Öffnen dieser Datei startet RStudio automatisch im richtigen Arbeitsverzeichnis.
Typischerweise legt man ein neues Projekt an, speichert in diesem Ordner die benötigten Dateien wie den Datensatz und das R-Skript aus der Kurswebsite und importiert den Datensatz dann mithilfe von Einlesefunktionen (z. B. aus readr oder haven), sodass er im Environment sichtbar wird. Ein häufiger Stolperstein sind Dateipfade: Oft geht das Skript davon aus, dass die Daten in einem Unterordner („data/…“) liegen. Liegt die Datei direkt im Projektordner, muss der Pfad entsprechend angepasst werden.
Arbeiten mit Skripten und Paketen
Das bereitgestellte R-Skript enthält den gesamten Code der Sitzung. Die Studierenden sollen diesen Code schrittweise ausführen und beobachten, welche Ausgaben der jeweilige Befehl erzeugt. Pakete werden üblicherweise am Anfang des Skripts mit library() geladen. Codezeilen lassen sich mit Strg+Enter (Windows) oder Cmd+Enter (Mac) ausführen. Für die Klausur müssen die Befehle nicht auswendig gelernt werden; wichtig ist das Verstehen und Interpretieren der erzeugten Tabellen, Kennwerte und Konfidenzintervalle.
