Moderation & Interaktion
Methoden der empirischen Kommunikations- und Medienforschung
Freie Universität Berlin
Fragen zur Übung?
Agenda
- Einführung
- Beispielstudie
- Dichotomer Moderator
- Quasi-metrischer Moderator
- Fazit
- Übungsaufgaben
Einführung
Was ist ein moderierter Effekt?
Beispiel: Lernen aus den Medien und die Wissenskluft-Hypothese
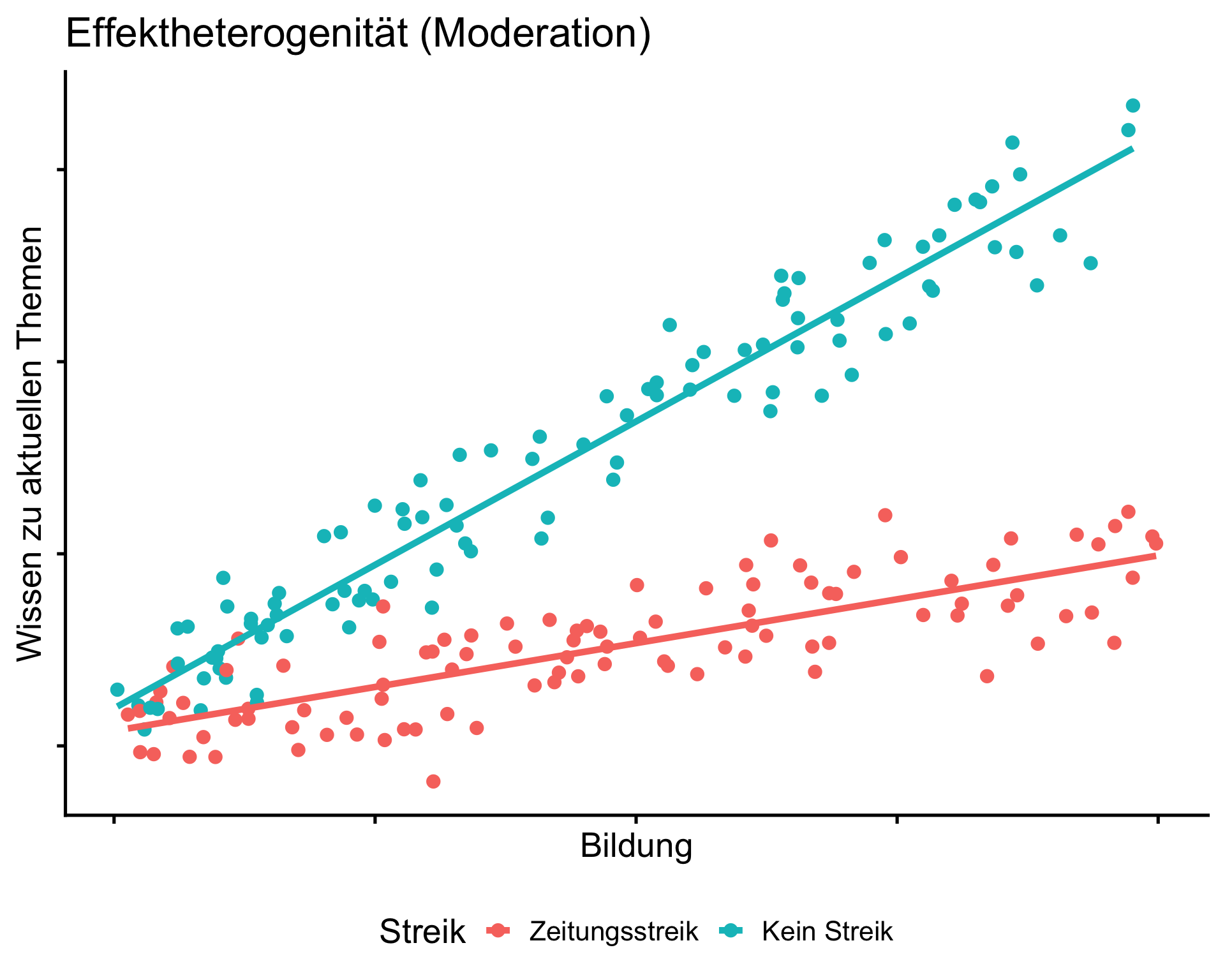
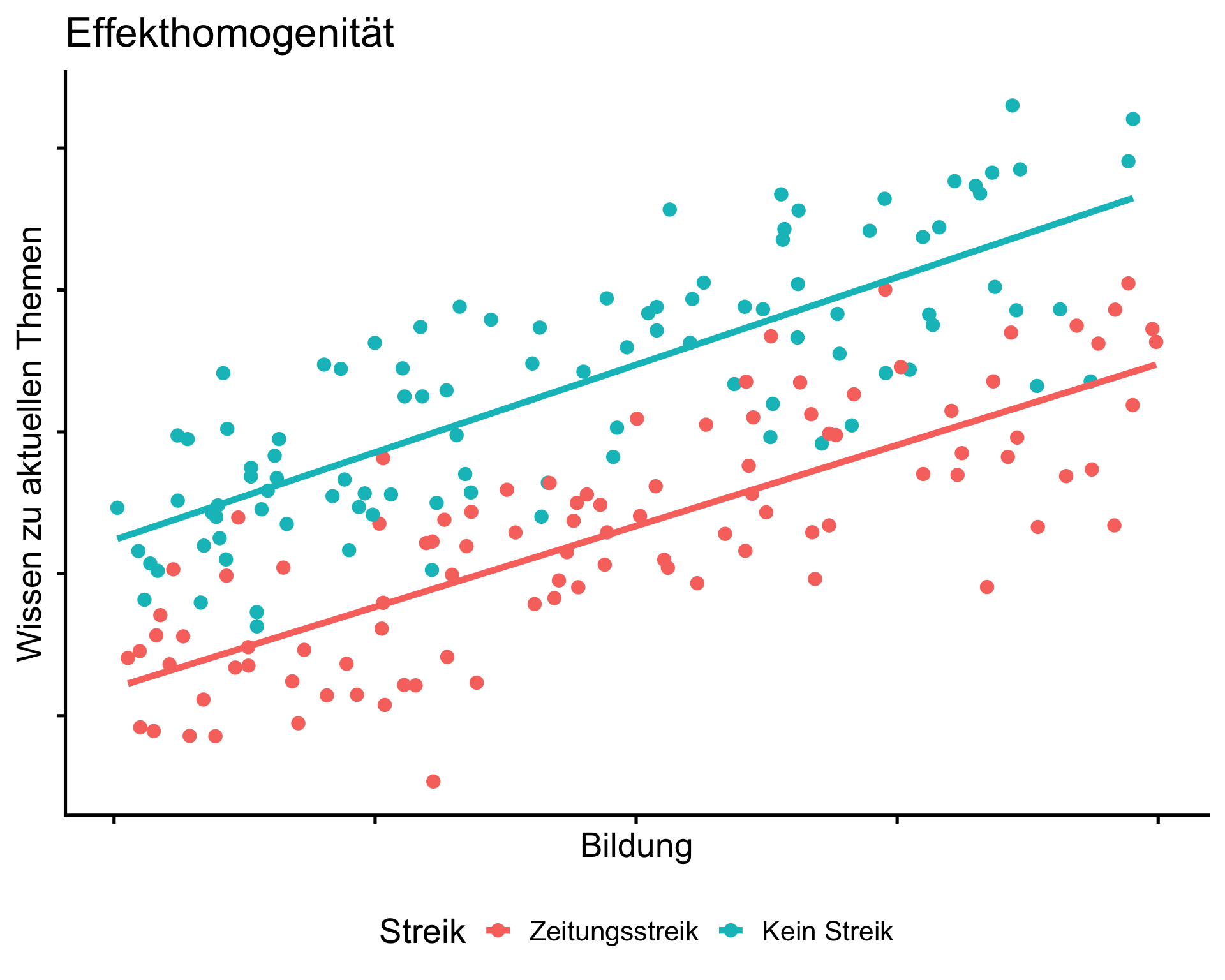
Was ist ein moderierter Effekt?
Original: Lernen aus den Medien und die Wissenskluft-Hypothese

Interaktion und Moderation
- Statistisch: Regressionskoeffizient eines Prädiktors ändert sich in Abhängigkeit der Werte eines anderen Prädiktors (Abschwächung der Additivitätsannahme)
- Begriffe: Interaktion und Moderation werden meist synonym verwendet (so auch hier).
- Begriffliche Traditionen:
- Interaktion zwischen Faktoren in einem mehrfaktoriellen Experimentaldesign
- Moderation des Effekts eines Prädiktors durch einen (gemessenen) Moderator
- Manchmal Bedeutungsunterschiede:
- Interaktionseffekt: Alle beteiligten Faktoren haben bereits für sich einen kausalen Effekt, bei gemeinsamen Auftreten ändert sich dieser Effekt.
- Effect modifier: Ein Moderator selbst hat keinen kausalen Effekt, er verändert lediglich den kausalen Effekt eines anderen Prädiktors.
- Prinzipiell könnten beliebig viele Variablen in einem Modell miteinander interagieren. Wir beschränken uns aber auf die zweifache Interaktion.
Einordnung in aktuelle Debatten
- Soziale Realität ist komplex, uniforme Medienwirkungen unrealistisch → Theorien und Modelle zur Effektheterogenität en vogue.
- Resonance model of political campaign effects (Iyengar & Simon, 2000)
- Differential susceptibility to media effects model (Valkenburg & Peter, 2013), Person-specific media effects (Valkenburg et al., 2021)
- Aber Theorien und Modelle sollen die Realität vereinfacht abbilden und möglichst allgemeingültig sein.
- Fuck nuance (Healy, 2017)
- A simple future for media effects research (Dienlin et al., 2025)
- und die theoretisch fundierte empirische Untersuchung und Modellierung von Heterogenität ist nicht so einfach
- Review Top PolSci Journals: “the execution of these models is often flawed and inferential errors are common” (Brambor et al., 2006)
- Precise answers to vague questions (Rohrer & Arslan, 2021)
Regressionsgleichung mit Moderation
- Wir beginnen mit einer einfachen Regressionsgleichung mit zwei Prädiktoren, \(X\) (z.B. Streik) und \(Z\) (z.B. Bildung)
\[Y = b_0 + b_1X + b_2Z + \epsilon\]
- Nun gehen wir davon aus, dass \(b_1\), der Effekt von \(X\) auf \(Y\), eine Funktion von \(Z\) ist
\[Y = b_0 + f(Z)X + b_2Z + \epsilon\]
- Die Funktion \(f(Z)\) sei definiert als lineare Funktion \(f(Z) = b_1 + b_3Z\)
\[Y = b_0 + (b_1 + b_3Z)X + b_2Z + \epsilon\]
- Durch Ausmultiplizieren erhalten wir einen Interaktionsterm \(XZ\), der einfach das Produkt von \(X\) und \(Z\) ist
\[Y = b_0 + b_1X + b_2Z + b_3XZ + \epsilon\]
Was bedeuten die Koeffizienten?
Regressionsgleichung \(Y = b_0 + b_1X + b_2Z + b_3XZ + \epsilon\)
- \(b_0\) (Intercept) ist der erwartete Wert von \(Y\), wenn \(X = 0\) und \(Z = 0\)
- z.B. Wissen von Personen, die geringste Bildung haben und keine Zeitung bekommen
- \(b_1\) ist der (konditionale) Effekt von \(X\), wenn \(Z = 0\)
- z.B. Effekt der Zeitungsverfügbarkeit auf Personen mit geringster Bildung
- \(b_2\) ist der (konditionale) Effekt von \(Z\), wenn \(X = 0\)
- z.B. Effekt des Anstiegs um 1 “Bildungspunkt” für Personen ohne Zeitung
- \(b_3\) ist der eigentliche Interaktionseffekt, d.h. die Differenz in \(b_1\), wenn \(Z\) sich um eine Einheit ändert
- z.B. Unterschied im Effekt der Zeitungsverfügbarkeit zwischen zwei Personen, die sich in Bildung um 1 unterscheiden.
Interpretation konditionaler Effekte
- Häufig nur Interpretation der statistischen Signifikanz von \(b_3\) — das ist theoretisch unbefriedigend!
- Auch die substanziellen Effekte berichten und interpretieren, z.B. durch
- Interpretation von Richtung und Betrag von \(b_3\)
- Schätzung der konditionalen Regressionskoeffizienten für (typische) Werte von \(Z\)
- Visualisierung der Modellvorhersagen für \(Y\) für (typische) Werte von \(Z\)
Wichtig: Bei Regressionsmodellen mit Interaktionseffekten \(XZ\) sind die Koeffizienten von \(X\) und \(Z\) nicht mehr unabhängig voneinander interpretierbar, d.h. die Koeffizienten sind nicht mehr unkonditional für alle Fälle \(n\) gültig!
Wichtig: Damit die konditionalen Koeffizienten überhaupt interpretierbar sind, muss der Wert 0 für alle an der Interaktion beteiligten Variablen interpretierbar sein (siehe Transformationen)!
Fragen?
Beispielstudie
Daten der heutigen Sitzung

Daten der heutigen Sitzung
- schwab: Experimentalbedingung Dialekt; Hochdeutsch (0), schwäbisch (1)
- atol: Attitude toward language; hier Einstellung zum Schwäbischen, Index aus stillos – stilvoll; missverständlich – eindeutig; unangenehm – angenehm; abgehackt – flüssig; hässlich – schön (Moderator, 1-5)
- gesamt: Gesamtbewertung des Politikers (Outcome-Variable, 1-5)
| schwab | gender | atol | gesamt |
|---|---|---|---|
| Hochdeutsch | männlich | 2.4 | 4 |
| Hochdeutsch | männlich | 3.6 | 4 |
| Hochdeutsch | weiblich | 2.6 | 4 |
| Schwäbisch | weiblich | 2.0 | 5 |
| Schwäbisch | weiblich | 3.8 | 4 |
| Schwäbisch | weiblich | 1.8 | 2 |
Stichprobe
| Variable | Hochdeutsch (n=146) | Schwäbisch (n=177) | Total (n=323) |
|---|---|---|---|
| gender [männlich], % | 44.5 | 43.5 | 44.0 |
| Mean age (SD) | 39.34 (18.53) | 40.16 (19.10) | 39.79 (18.82) |
| Mean atol (SD) | 3.33 (0.77) | 3.29 (0.79) | 3.31 (0.78) |
| Mean gesamt (SD) | 3.84 (0.79) | 3.59 (0.90) | 3.71 (0.86) |
Dichotomer Moderator (hier: Gender)
Effekt des Dialekts (Kontrolle: Gender)
| Parameter | Coefficient | 95% CI | t(320) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 3.99 | (3.83, 4.15) | 49.21 | < .001 | |
| schwab (Schwäbisch) | -0.25 | (-0.44, -0.07) | -2.69 | 0.007 | |
| gender (männlich) | -0.33 | (-0.52, -0.15) | -3.53 | < .001 | |
| R2 (adj.) | 0.05 |
Effekt des Dialekts (Kontrolle: Gender)
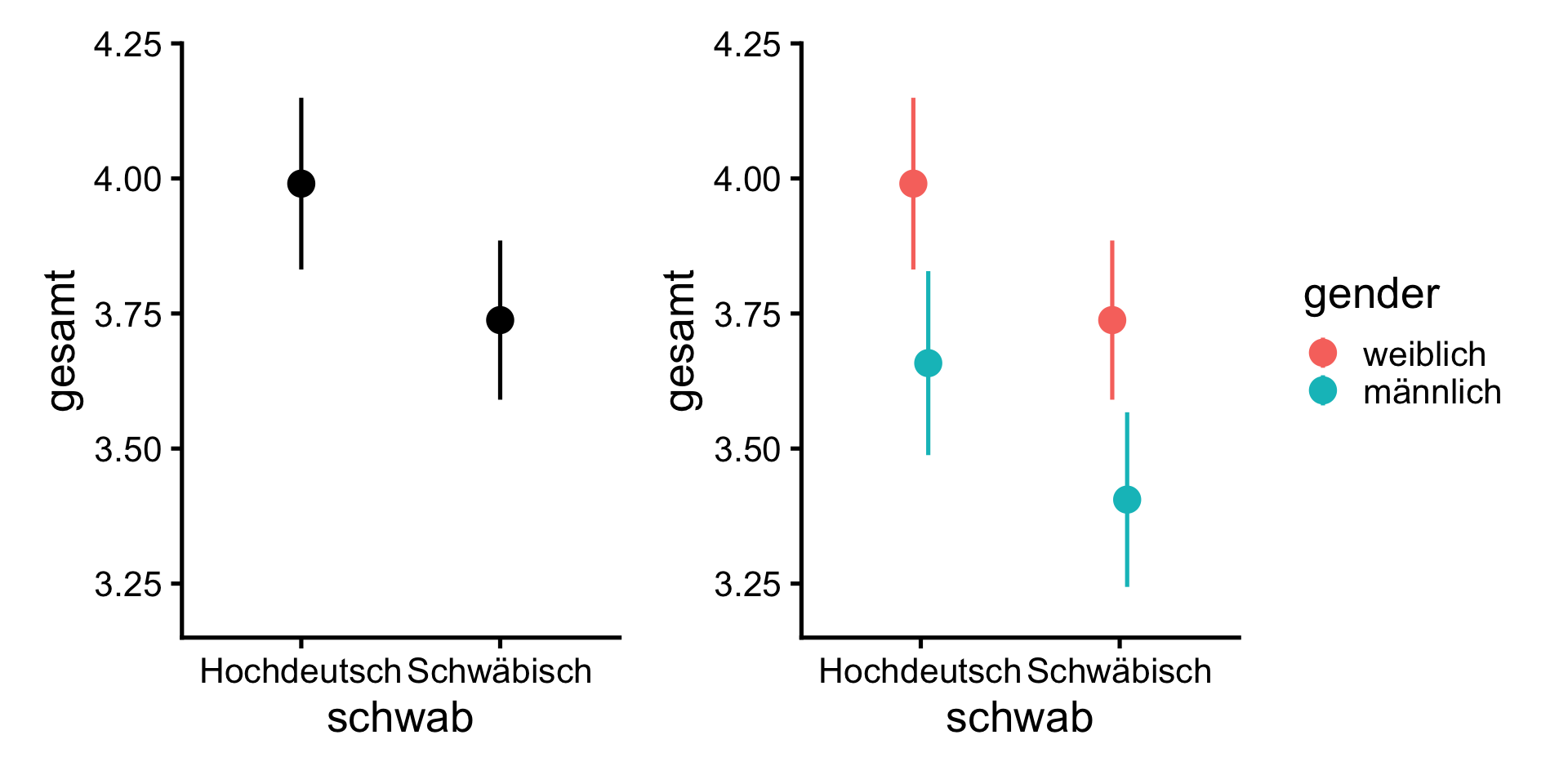
Moderation des Dialekt-Effekts durch Gender
- In R werden Interaktionsterme direkt in die Modellformel für
lm()geschrieben:y ~ x * z
| Parameter | Coefficient | 95% CI | t(319) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 3.98 | (3.79, 4.16) | 42.58 | < .001 | |
| schwab (Schwäbisch) | -0.23 | (-0.47, 0.02) | -1.79 | 0.074 | |
| gender (männlich) | -0.30 | (-0.57, -0.02) | -2.13 | 0.034 | |
| schwab (Schwäbisch) × gender (männlich) | -0.06 | (-0.43, 0.31) | -0.33 | 0.743 | |
| R2 (adj.) | 0.05 |
- \(b_0\) (Intercept): Mittelwert für Frauen mit Hochdeutsch-Stimulus
- \(b_1\) (schwab (Schwäbisch)): Dialekt-Effekt für Frauen
- \(b_2\) (gender (männlich)): Unterschied zwischen Frauen (Referenz) und Männern nach Hochdeutsch-Stimulus
- \(b_3\) (schwab (Schwäbisch) × gender (männlich)): Unterschied des Dialekt-Effekts für Männer und Frauen
Moderation des Dialekt-Effekts durch Gender
| Parameter | Coefficient | t(320) | p |
|---|---|---|---|
| (Intercept) | 3.99 | 49.21 | < .001 |
| schwab (Schwäbisch) | -0.25 | -2.69 | 0.007 |
| gender (männlich) | -0.33 | -3.53 | < .001 |
| Parameter | Coefficient | t(319) | p |
|---|---|---|---|
| (Intercept) | 3.98 | 42.58 | < .001 |
| schwab (Schwäbisch) | -0.23 | -1.79 | 0.074 |
| gender (männlich) | -0.30 | -2.13 | 0.034 |
| schwab (Schwäbisch) × gender (männlich) | -0.06 | -0.33 | 0.743 |
- Koeffizienten haben andere Bedeutungen!
Moderation des Dialekt-Effekts durch Gender
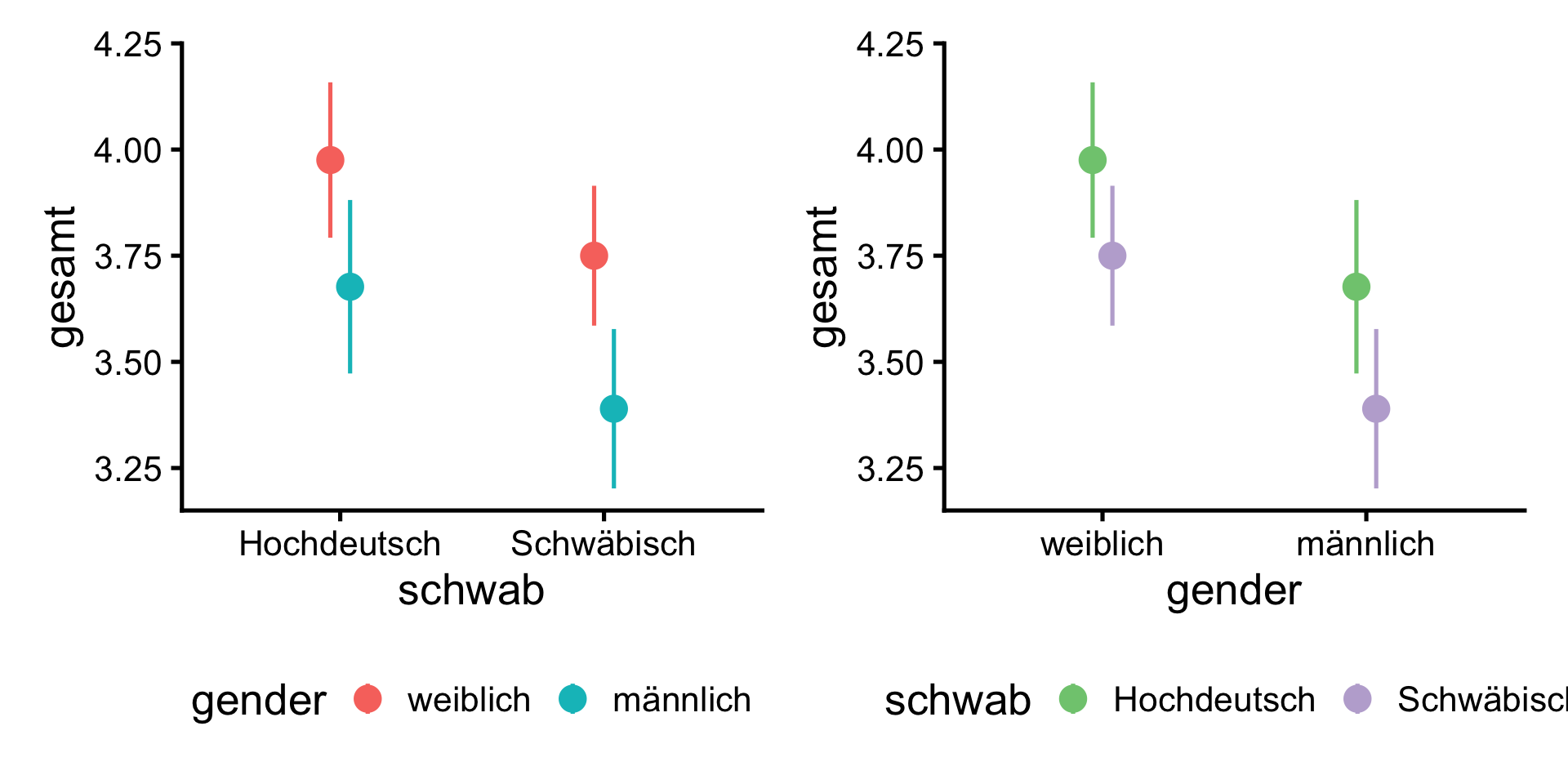
Moderation des Dialekt-Effekts durch Gender
| Parameter | Coefficient | 95% CI | t(319) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 3.98 | (3.79, 4.16) | 42.58 | < .001 | |
| schwab (Schwäbisch) | -0.23 | (-0.47, 0.02) | -1.79 | 0.074 | |
| gender (männlich) | -0.30 | (-0.57, -0.02) | -2.13 | 0.034 | |
| schwab (Schwäbisch) × gender (männlich) | -0.06 | (-0.43, 0.31) | -0.33 | 0.743 | |
| R2 (adj.) | 0.05 |
- Der negative Effekt des schwäbischen Dialekts im Vergleich zu einem hochdeutschen gesprochenen Interview fällt in der Stichprobe für Männer um 0.06 Skalenpunkte stärker aus als für Frauen. Diese Differenz zwischen den Effekten für Männer und Frauen ist allerdings nicht statistisch signifikant: \(b = -0.06\) , \(t(319) = 0.33\), \(p = .743\)).
Zwischenfazit
- Moderationsanalysen mit dichotomen Moderatoren sind technisch leicht durchführbar, erfordern aber eine neue Interpretation
- Die Interpretation der statistischen Signifikanz der Interaktionsterme ist einfach, die substanzielle Interpretation schwieriger
- Durch Hinzunahme des Interaktionsterms quantifizieren die Koeffizienten der beteiligten Prädiktoren konditionale Effekte in der Referenzgruppe (!)
Fragen?
Quasi-metrischer Moderator
Quasi-metrischer Moderator (hier: AtoL)
- Anstelle eines dichotomen Moderators kann auch ein metrischer Moderator berücksichtigt werden
- Idee: Effekt verändert sich als (lineare) Funktion des Moderators
- Beispiel: Voreinstellung gegenüber dem schwäbischen Dialekt (atol).
- Hypothese: Je positiver die Einstellung zum schwäbischen Dialekt bei einer Versuchsperson, desto positiver (bzw. weniger negativ) ist der Effekt des Dialekts.
Effekt des Dialekts (Kontrolle: AtoL)
| Parameter | Coefficient | 95% CI | t(320) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 3.41 | (2.99, 3.83) | 15.93 | < .001 | |
| schwab (Schwäbisch) | -0.24 | (-0.43, -0.06) | -2.56 | 0.011 | |
| atol | 0.13 | (0.01, 0.25) | 2.12 | 0.034 | |
| R2 (adj.) | 0.03 |
Effekt des Dialekts (Kontrolle: AtoL)
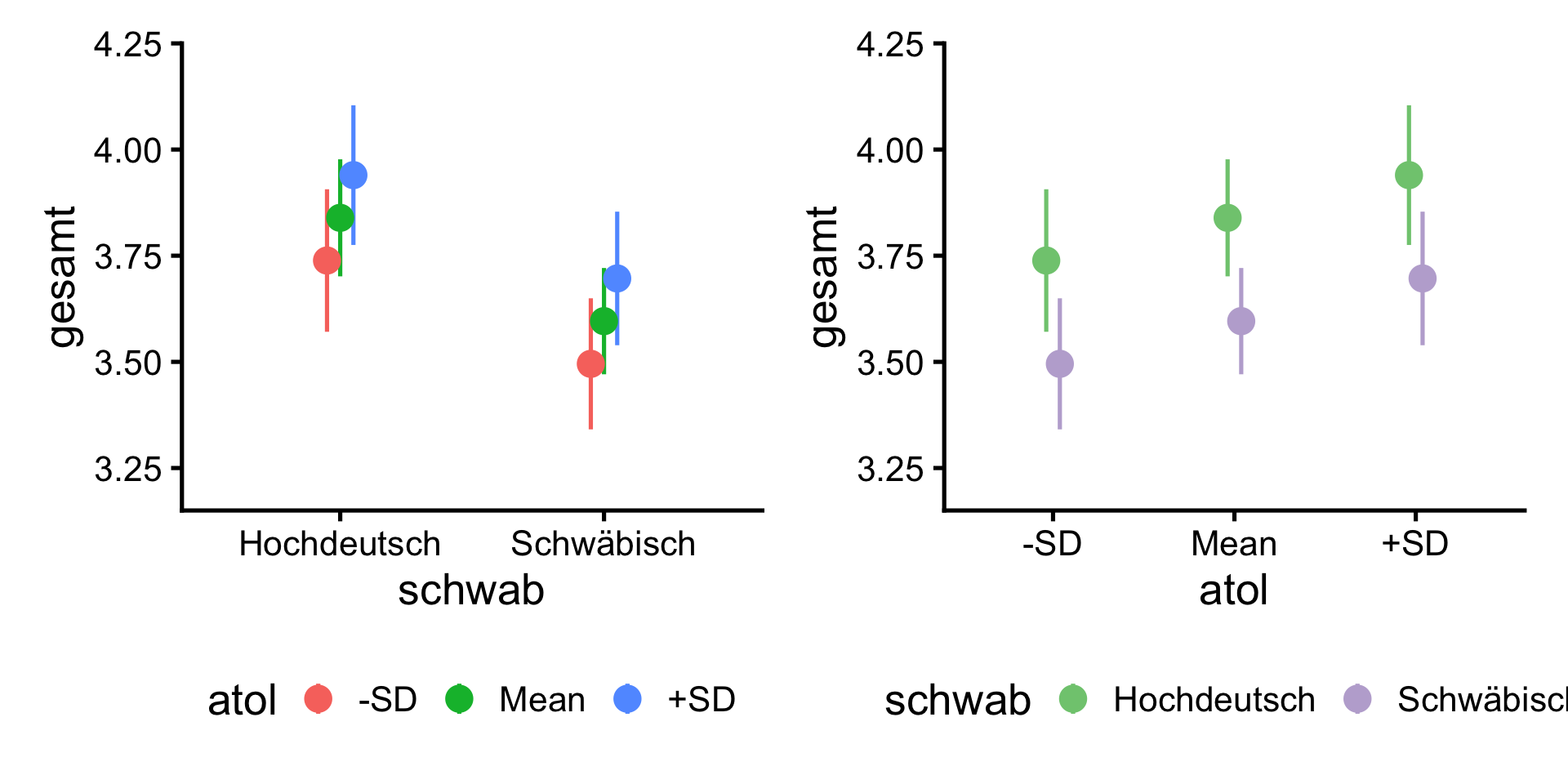
Moderation des Dialekt-Effekts durch AtoL
| Parameter | Coefficient | 95% CI | t(319) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 4.06 | (3.45, 4.66) | 13.11 | < .001 | |
| schwab (Schwäbisch) | -1.39 | (-2.20, -0.58) | -3.37 | < .001 | |
| atol | -0.06 | (-0.24, 0.11) | -0.71 | 0.481 | |
| schwab (Schwäbisch) × atol | 0.34 | (0.11, 0.58) | 2.85 | 0.005 | |
| R2 (adj.) | 0.05 |
- \(b_0\) (Intercept): Mittelwert für Personen mit AtoL = 0 und Hochdeutsch-Stimulus
- \(b_1\) (schwab (Schwäbisch)): Dialekt-Effekt für Personen mit AtoL = 0
- \(b_2\) (atol): Unterschied zwischen Personen mit 1 Punkt Unterschied auf AtoL-Skala nach Hochdeutsch-Stimulus
- \(b_3\) (schwab (Schwäbisch) × atol): Unterschied des Dialekt-Effekts zwischen Personen mit 1 Punkt Unterschied auf AtoL-Skala
- Personen mit AtoL = 0 — Außerhalb der gültigen Werte der Skala
Moderation des Dialekt-Effekts durch AtoL
| Parameter | Coefficient | 95% CI | t(319) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 3.84 | (3.71, 3.98) | 55.26 | < .001 | |
| schwab (Schwäbisch) | -0.24 | (-0.43, -0.06) | -2.61 | 0.010 | |
| atol c | -0.06 | (-0.24, 0.11) | -0.71 | 0.481 | |
| schwab (Schwäbisch) × atol c | 0.34 | (0.11, 0.58) | 2.85 | 0.005 | |
| R2 (adj.) | 0.05 |
- \(b_0\) (Intercept): Mittelwert für Personen mit durchschnittlicher AtoL und Hochdeutsch-Stimulus
- \(b_1\) (schwab (Schwäbisch)): Dialekt-Effekt für Personen mit durchschnittlicher AtoL
- \(b_2\) (atol): Unterschied zwischen Personen mit 1 Punkt Unterschied auf AtoL-Skala nach Hochdeutsch-Stimulus
- \(b_3\) (schwab (Schwäbisch) × atol): Unterschied des Dialekt-Effekts zwischen Personen mit 1 Punkt Unterschied auf AtoL-Skala
Moderation des Dialekt-Effekts durch AtoL
| Parameter | Coefficient | t(320) | p |
|---|---|---|---|
| (Intercept) | 3.41 | 15.93 | < .001 |
| schwab (Schwäbisch) | -0.24 | -2.56 | 0.011 |
| atol | 0.13 | 2.12 | 0.034 |
| Parameter | Coefficient | t(319) | p |
|---|---|---|---|
| (Intercept) | 3.84 | 55.26 | < .001 |
| schwab (Schwäbisch) | -0.24 | -2.61 | 0.010 |
| atol c | -0.06 | -0.71 | 0.481 |
| schwab (Schwäbisch) × atol c | 0.34 | 2.85 | 0.005 |
- Koeffizienten haben andere Bedeutungen!
Moderation des Dialekt-Effekts durch AtoL
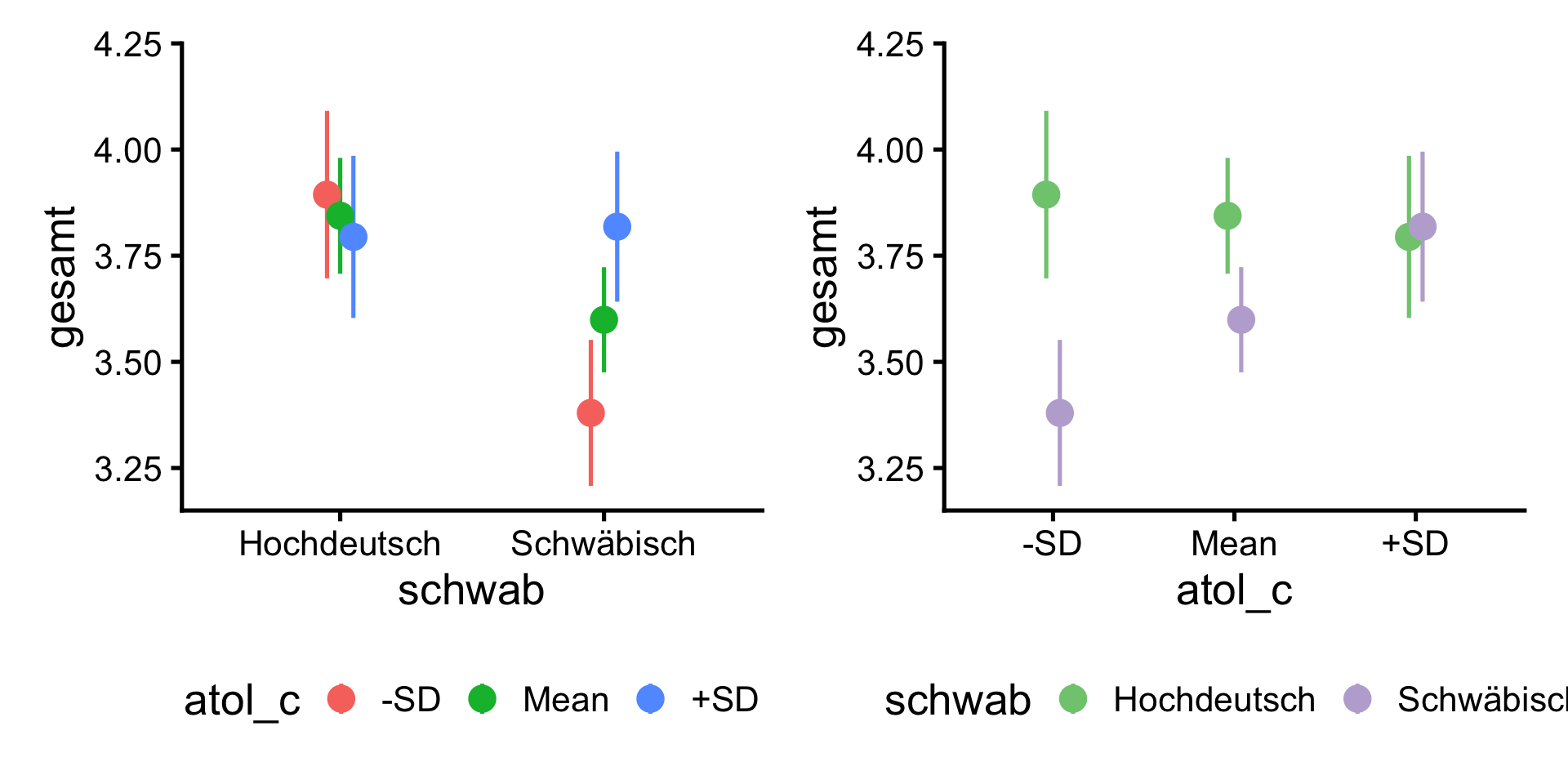
Moderation des Dialekt-Effekts durch AtoL
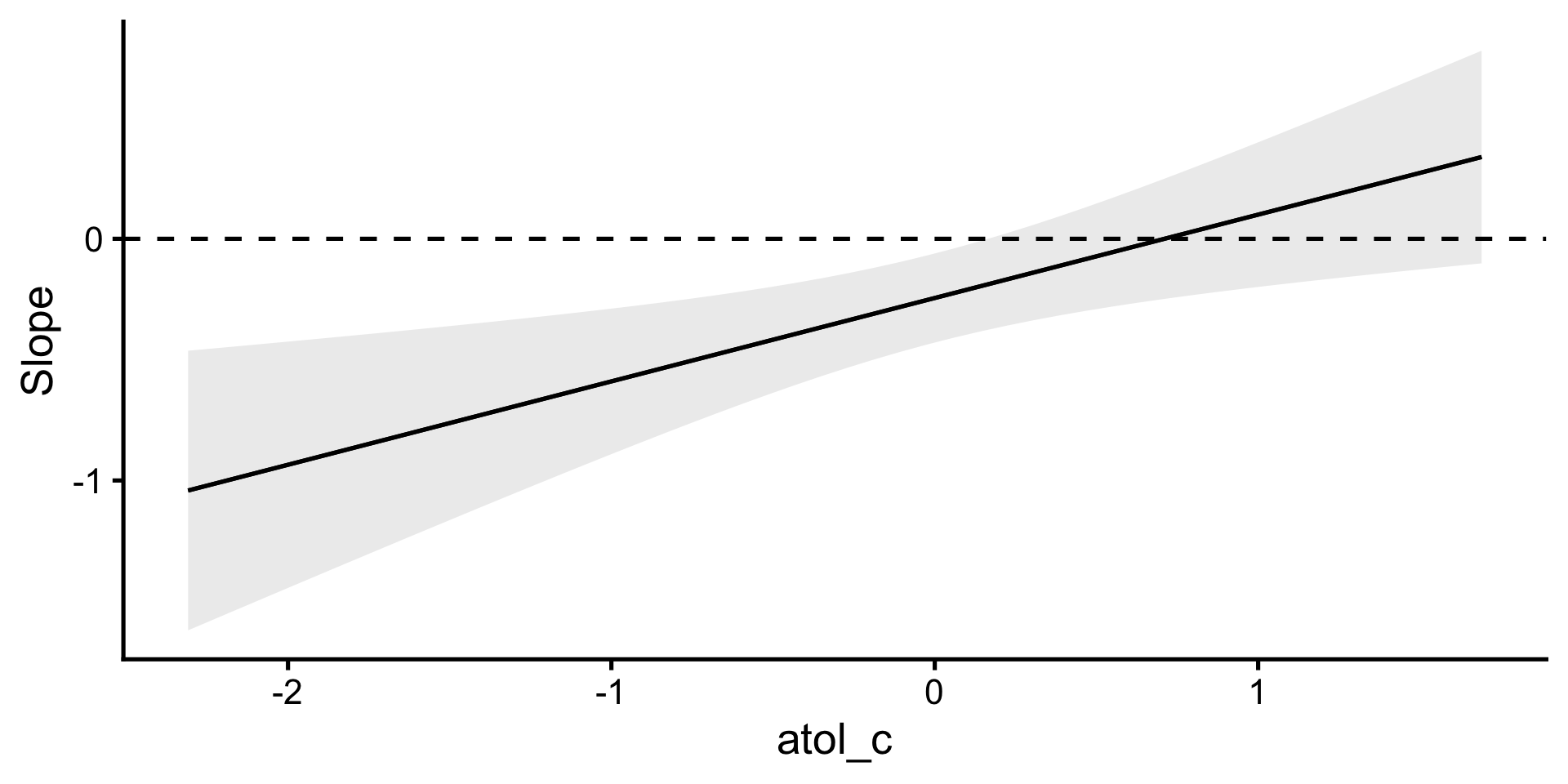
Moderation des Dialekt-Effekts durch AtoL
| Parameter | Coefficient | 95% CI | t(319) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 3.84 | (3.71, 3.98) | 55.26 | < .001 | |
| schwab (Schwäbisch) | -0.24 | (-0.43, -0.06) | -2.61 | 0.010 | |
| atol c | -0.06 | (-0.24, 0.11) | -0.71 | 0.481 | |
| schwab (Schwäbisch) × atol c | 0.34 | (0.11, 0.58) | 2.85 | 0.005 | |
| R2 (adj.) | 0.05 |
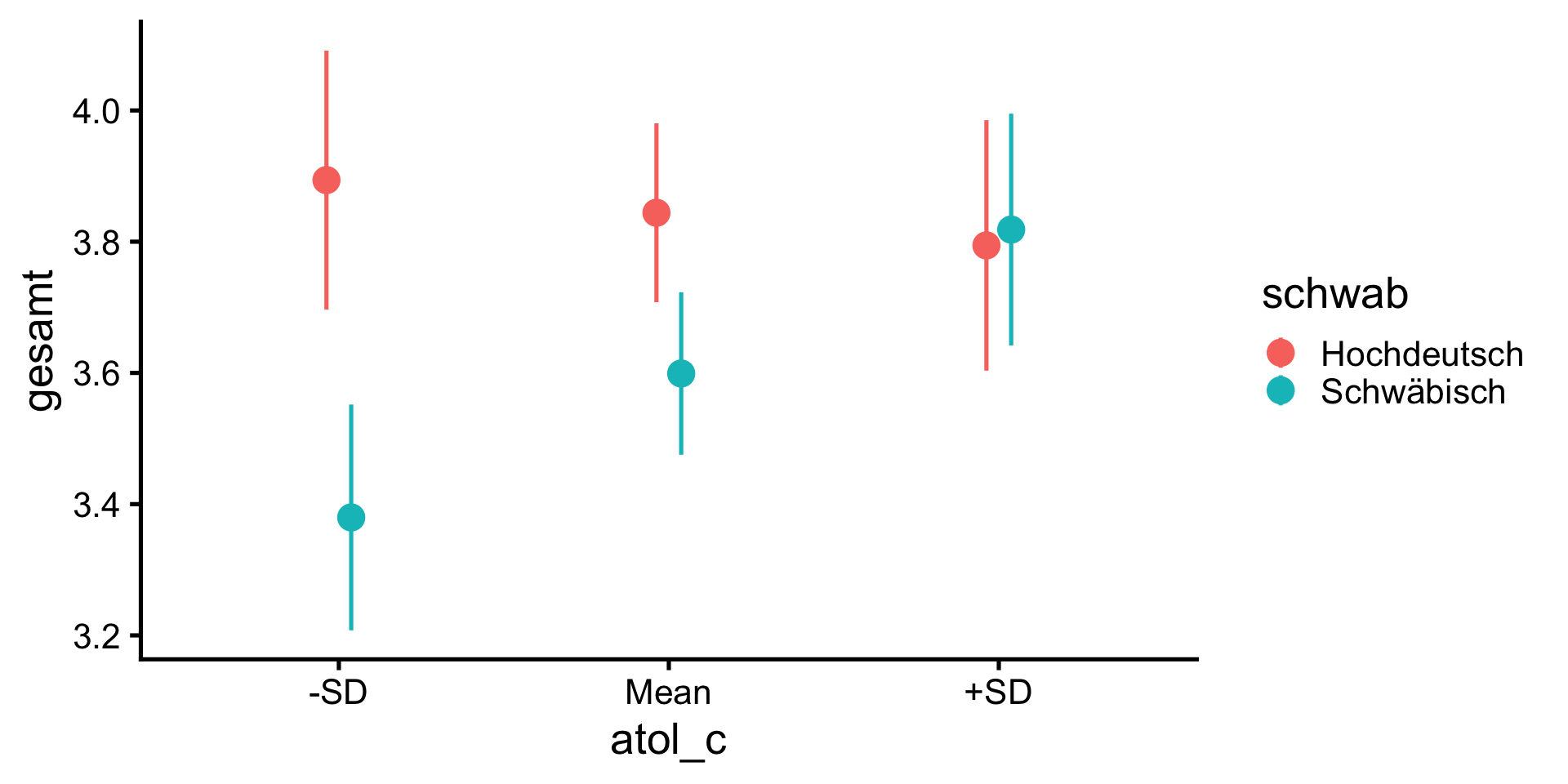
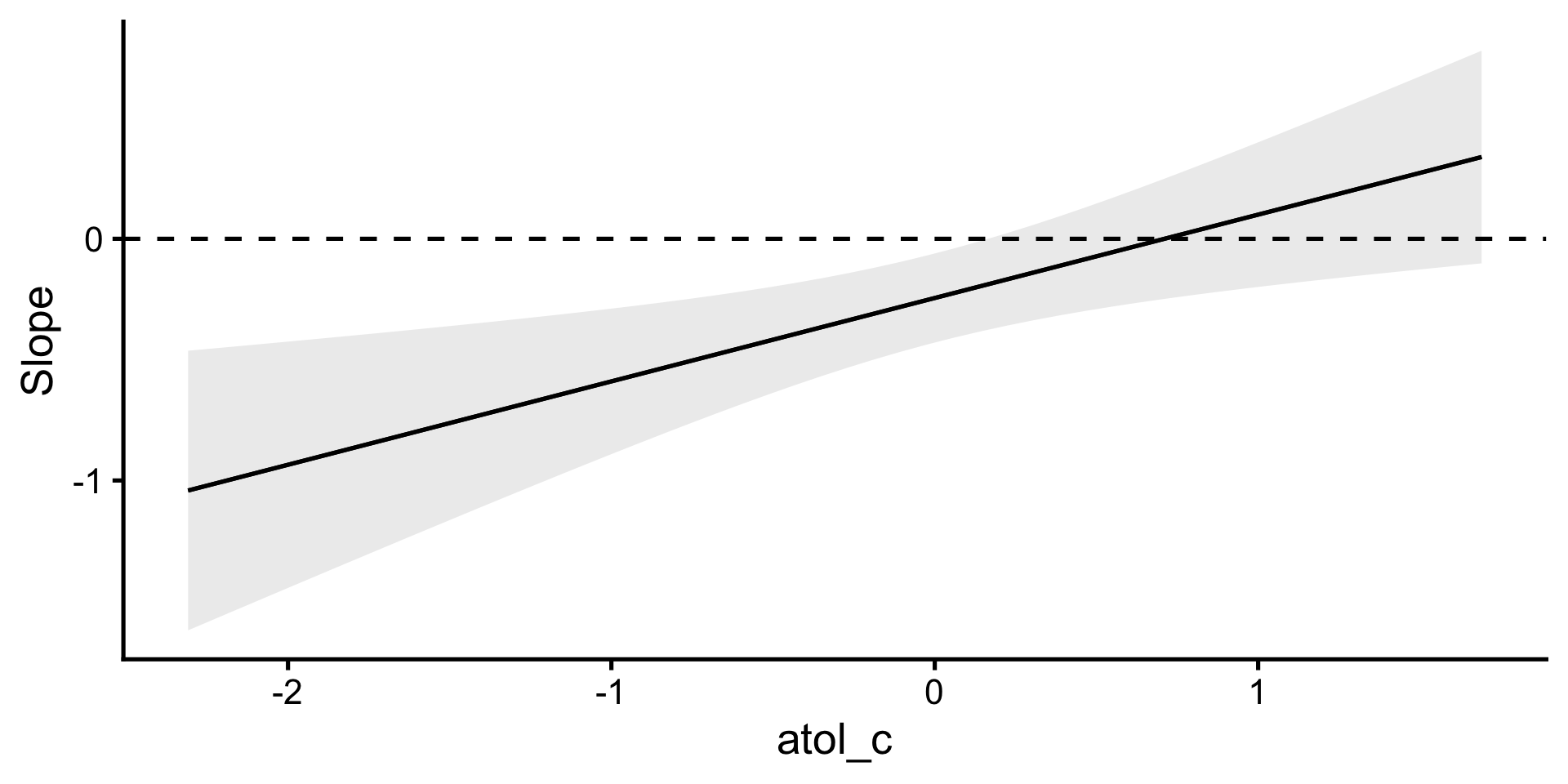
Moderation des Dialekt-Effekts durch AtoL
Der negative Effekt des schwäbischen Dialekts auf die Bewertung des Politikers wird durch die Einstellung zum Schwäbischen moderiert. Für Personen, die das Schwäbische gut finden, besteht kaum ein Unterschied zwischen den Interview-Versionen. Je schlechter eine Person das Schwäbische allgemein bewertet, desto negativer fällt der Effekt des Dialekts aus. Mit jedem Punkt weniger auf der AtoL-Skala verstärkt sich der negative Effekt um 0.34 Punkte: \(b = 0.34\), \(t(319) = 2.85\), \(p = .005\).
Fragen?
Fazit
Lineare Modelle mit Moderation sind in der Regel sehr leicht zu spezifizieren, aber zumeist deutlich schwieriger substanziell zu interpretieren (außer Signifikanz des Interaktionseffekts)
Auch wenn die Regressionstabelle optisch sehr ähnlich aussieht, ändert sich Interpretation grundsätzlich; immer zusätzliche Visualisierungen des Modells betrachten.
Fragen?
Übungsaufgaben
Fragen?
Nächste Einheit
Digitale Verhaltensdaten und Webtracking
Danke
Marko Bachl