7 Multiple lineare Regression

7.1 Folien

7.2 Daten der heutigen Sitzung

(Van Erkel, 2020; Van Erkel & Van Aelst, 2021)

7.3 Code und Ausgaben aus der Vorlesung

Laden der relevanten Pakete

library(report) # Einfaches Erstellen von statistischen Berichten
library(marginaleffects) # Vorhersagen aus Regressionsmodellen
library(modelsummary) # Darstellung von Regressionsmodellen
library(parameters) # Darstellung von Regressionsmodellen


Attaching package: 'parameters'

The following object is masked from 'package:modelsummary':

    supported_models

library(performance) # Prüfen der Voraussetzungen
library(tidyverse) # Datenmanagement und Visualisierung: https://www.tidyverse.org/

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.6
✔ forcats   1.0.1     ✔ stringr   1.6.0
✔ ggplot2   4.0.1     ✔ tibble    3.3.0
✔ lubridate 1.9.4     ✔ tidyr     1.3.1
✔ purrr     1.2.0

── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Lesen und Aufbereiten des Datensatz von Van Erkel & Van Aelst

d <- haven::read_stata(here::here("data/Vanerkel_Vanaelst_2021.dta")) |>
  rename(
    Political_knowledge = PK,
    Personalized_news = personalized_news,
    Radio = News_channels_w4_1,
    Television = News_channels_w4_2,
    Newspapers = News_channels_w4_3,
    Online_news_sites = News_channels_w4_4,
    Twitter = News_channels_w4_5,
    Facebook = News_channels_w4_6
  ) |>
  mutate(
    Gender = as_factor(Gender),
    Education = as_factor(Education),
    trad = factor(trad, labels = c(
      "traditional news diet: no",
      "traditional news diet: yes"
    ))
  )

Einfaches Modell mit zwei Prädiktoren

simple_model <- lm(Political_knowledge ~ Age + Newspapers, data = d) |>
  report_table(metrics = "R2_adj")
simple_model

Parameter   | Coefficient |       95% CI | t(990) |      p | Std. Coef.
-----------------------------------------------------------------------
(Intercept) |        0.99 | [0.67, 1.31] |   6.07 | < .001 |   2.92e-16
Age         |        0.02 | [0.02, 0.03] |   8.24 | < .001 |       0.24
Newspapers  |        0.22 | [0.18, 0.27] |   9.31 | < .001 |       0.28
            |             |              |        |        |           
R2 (adj.)   |             |              |        |        |           

Parameter   | Std. Coef. 95% CI |  Fit
--------------------------------------
(Intercept) |     [-0.06, 0.06] |     
Age         |     [ 0.19, 0.30] |     
Newspapers  |     [ 0.22, 0.33] |     
            |                   |     
R2 (adj.)   |                   | 0.16

simple_model

Parameter   | Coefficient |       95% CI | t(990) |      p | Std. Coef.
-----------------------------------------------------------------------
(Intercept) |        0.99 | [0.67, 1.31] |   6.07 | < .001 |   2.92e-16
Age         |        0.02 | [0.02, 0.03] |   8.24 | < .001 |       0.24
Newspapers  |        0.22 | [0.18, 0.27] |   9.31 | < .001 |       0.28
            |             |              |        |        |           
R2 (adj.)   |             |              |        |        |           

Parameter   | Std. Coef. 95% CI |  Fit
--------------------------------------
(Intercept) |     [-0.06, 0.06] |     
Age         |     [ 0.19, 0.30] |     
Newspapers  |     [ 0.22, 0.33] |     
            |                   |     
R2 (adj.)   |                   | 0.16

Regression mit binärem Prädiktor Gender

lm(Political_knowledge ~ Gender, data = d) |>
  report_table(include_effectsize = FALSE, metrics = "R2")

Parameter       | Coefficient |         95% CI | t(991) |      p |  Fit
-----------------------------------------------------------------------
(Intercept)     |        3.44 | [ 3.33,  3.55] |  60.48 | < .001 |     
Gender [female] |       -0.84 | [-1.00, -0.67] | -10.14 | < .001 |     
                |             |                |        |        |     
R2              |             |                |        |        | 0.09

Kontraste des Faktors Bildung: Niedrige Bildung als Referenz (Default)

contrasts(d$Education) |>
  as.data.frame() |>
  rownames_to_column("Zugehörigkeit")

  Zugehörigkeit Middle High
1         Lower      0    0
2        Middle      1    0
3          High      0    1

Mittelwerte Politisches Wissen nach Bildung

d |>
  summarise(
    M = mean(Political_knowledge),
    .by = Education
  ) |>
  arrange(Education) |>
  spread(Education, M)

# A tibble: 1 × 3
  Lower Middle  High
  <dbl>  <dbl> <dbl>
1  2.58   2.97  3.25

Regression Politisches Wissen nach Bildung mit niedriger Bildung als Referenz

lm(Political_knowledge ~ Education, data = d) |>
  report_table(include_effectsize = FALSE, metrics = "R2_adj")

Parameter          | Coefficient |       95% CI | t(990) |      p |  Fit
------------------------------------------------------------------------
(Intercept)        |        2.58 | [2.35, 2.81] |  22.39 | < .001 |     
Education [Middle] |        0.39 | [0.13, 0.65] |   2.92 | 0.004  |     
Education [High]   |        0.67 | [0.41, 0.93] |   5.09 | < .001 |     
                   |             |              |        |        |     
R2 (adj.)          |             |              |        |        | 0.03

Kontraste des Faktors Bildung: Mittlere Bildung als Referenz

relevel(d$Education, "Middle") |>
  contrasts() |>
  as.data.frame() |>
  rownames_to_column("Zugehörigkeit")

  Zugehörigkeit Lower High
1        Middle     0    0
2         Lower     1    0
3          High     0    1

Regression Politisches Wissen nach Bildung mit mittlerer Bildung als Referenz

d$Education <- relevel(d$Education, "Middle")
lm(Political_knowledge ~ Education, data = d) |>
  report_table(include_effectsize = FALSE, metrics = "R2_adj")

Parameter         | Coefficient |         95% CI | t(990) |      p |  Fit
-------------------------------------------------------------------------
(Intercept)       |        2.97 | [ 2.84,  3.10] |  44.41 | < .001 |     
Education [Lower] |       -0.39 | [-0.65, -0.13] |  -2.92 | 0.004  |     
Education [High]  |        0.28 | [ 0.10,  0.46] |   3.03 | 0.002  |     
                  |             |                |        |        |     
R2 (adj.)         |             |                |        |        | 0.03

d$Education <- relevel(d$Education, "Lower")

Post-Hoc-Vergleich

lm(Political_knowledge ~ Education, data = d) |>
  avg_comparisons(
    variables = list(Education = "pairwise")
  )


       Contrast Estimate Std. Error    z Pr(>|z|)    S  2.5 % 97.5 %
 High - Lower      0.669      0.131 5.09  < 0.001 21.4 0.4109  0.926
 High - Middle     0.279      0.092 3.03  0.00241  8.7 0.0988  0.459
 Middle - Lower    0.389      0.133 2.92  0.00348  8.2 0.1282  0.651

Term: Education
Type: response

Post-Hoc-Vergleich mit Anpassung der p-Werte und Konfidenzintervalle

lm(Political_knowledge ~ Education, data = d) |>
  avg_comparisons(
    variables = list(Education = "pairwise")
  ) |>
  hypotheses(multcomp = "bonferroni")


 Estimate Std. Error    z Pr(>|z|)    S  2.5 % 97.5 %
    0.669      0.131 5.09  < 0.001 19.8 0.3619  0.975
    0.279      0.092 3.03  0.00724  7.1 0.0645  0.494
    0.389      0.133 2.92  0.01045  6.6 0.0785  0.700

Term: Education

Modelle 1 und 4 schätzen

m1 <- lm(Political_knowledge ~ Radio + Television + Newspapers + Online_news_sites + Twitter +
  Facebook + Gender + Age + Education + Political_interest, data = d)

m4 <- lm(Political_knowledge ~ Radio + Television + Newspapers + Online_news_sites + Twitter +
  Facebook + Gender + Age + Education + Political_interest + Information_overload, data = d)

Modelle 1 und 4 wie im Artikel darstellen

modelsummary(list("Model 1" = m1, "Model 4" = m4),
  estimate = "{estimate} ({std.error}){stars}",
  statistic = NULL,
  gof_map = c("nobs", "adj.r.squared"),
  fmt = fmt_decimal(digits = 2, pdigits = 3)
)

	Model 1	Model 4
(Intercept)	0.46 (0.22)*	0.67 (0.23)**
Radio	-0.01 (0.02)	-0.01 (0.02)
Television	0.08 (0.03)**	0.09 (0.03)**
Newspapers	0.08 (0.02)***	0.08 (0.02)***
Online_news_sites	0.06 (0.02)**	0.06 (0.02)**
Twitter	-0.06 (0.04)	-0.05 (0.04)
Facebook	-0.07 (0.02)***	-0.07 (0.02)***
Genderfemale	-0.48 (0.07)***	-0.46 (0.07)***
Age	0.02 (0.00)***	0.02 (0.00)***
EducationMiddle	0.28 (0.11)*	0.27 (0.11)*
EducationHigh	0.48 (0.11)***	0.48 (0.11)***
Political_interest	0.18 (0.01)***	0.17 (0.01)***
Information_overload		-0.03 (0.01)**
Num.Obs.	993	993
R2 Adj.	0.371	0.376

Ausführliche Regressionstabelle zu Modell 4

m4 |>
  report_table(metrics = "R2_adj")

Parameter            | Coefficient |         95% CI | t(980) |      p
---------------------------------------------------------------------
(Intercept)          |        0.67 | [ 0.21,  1.12] |   2.90 | 0.004 
Radio                |   -7.45e-03 | [-0.05,  0.04] |  -0.34 | 0.736 
Television           |        0.09 | [ 0.03,  0.15] |   2.80 | 0.005 
Newspapers           |        0.08 | [ 0.04,  0.13] |   3.46 | < .001
Online news sites    |        0.06 | [ 0.02,  0.11] |   2.73 | 0.006 
Twitter              |       -0.05 | [-0.13,  0.02] |  -1.37 | 0.171 
Facebook             |       -0.07 | [-0.11, -0.03] |  -3.38 | < .001
Gender [female]      |       -0.46 | [-0.60, -0.32] |  -6.34 | < .001
Age                  |        0.02 | [ 0.01,  0.02] |   6.03 | < .001
Education [Middle]   |        0.27 | [ 0.06,  0.48] |   2.48 | 0.013 
Education [High]     |        0.48 | [ 0.26,  0.69] |   4.27 | < .001
Political interest   |        0.17 | [ 0.14,  0.20] |  11.79 | < .001
Information overload |       -0.03 | [-0.05, -0.01] |  -3.03 | 0.003 
                     |             |                |        |       
R2 (adj.)            |             |                |        |       

Parameter            | Std. Coef. | Std. Coef. 95% CI |  Fit
------------------------------------------------------------
(Intercept)          |      -0.08 |    [-0.22,  0.06] |     
Radio                |  -9.45e-03 |    [-0.06,  0.05] |     
Television           |       0.08 |    [ 0.03,  0.14] |     
Newspapers           |       0.10 |    [ 0.04,  0.16] |     
Online news sites    |       0.08 |    [ 0.02,  0.14] |     
Twitter              |      -0.04 |    [-0.09,  0.02] |     
Facebook             |      -0.10 |    [-0.16, -0.04] |     
Gender [female]      |      -0.34 |    [-0.44, -0.23] |     
Age                  |       0.17 |    [ 0.12,  0.23] |     
Education [Middle]   |       0.20 |    [ 0.04,  0.35] |     
Education [High]     |       0.35 |    [ 0.19,  0.51] |     
Political interest   |       0.34 |    [ 0.28,  0.39] |     
Information overload |      -0.08 |    [-0.13, -0.03] |     
                     |            |                   |     
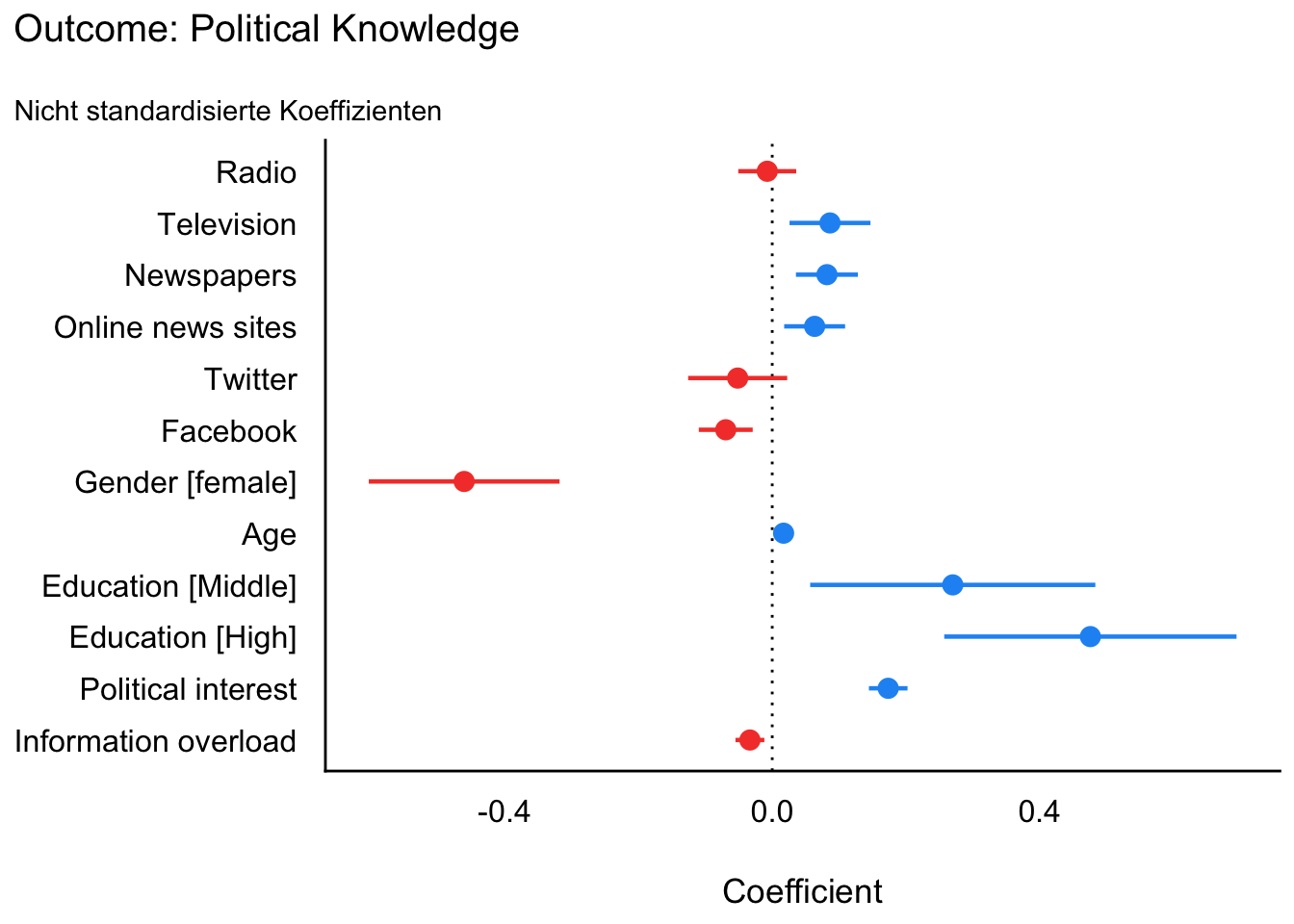
R2 (adj.)            |            |                   | 0.38

Koeffizientenplot mit nicht standardisierten Koeffizienten

m4 |>
  parameters() |>
  plot() +
  ggtitle("Outcome: Political Knowledge",
    subtitle = "Nicht standardisierte Koeffizienten"
  )

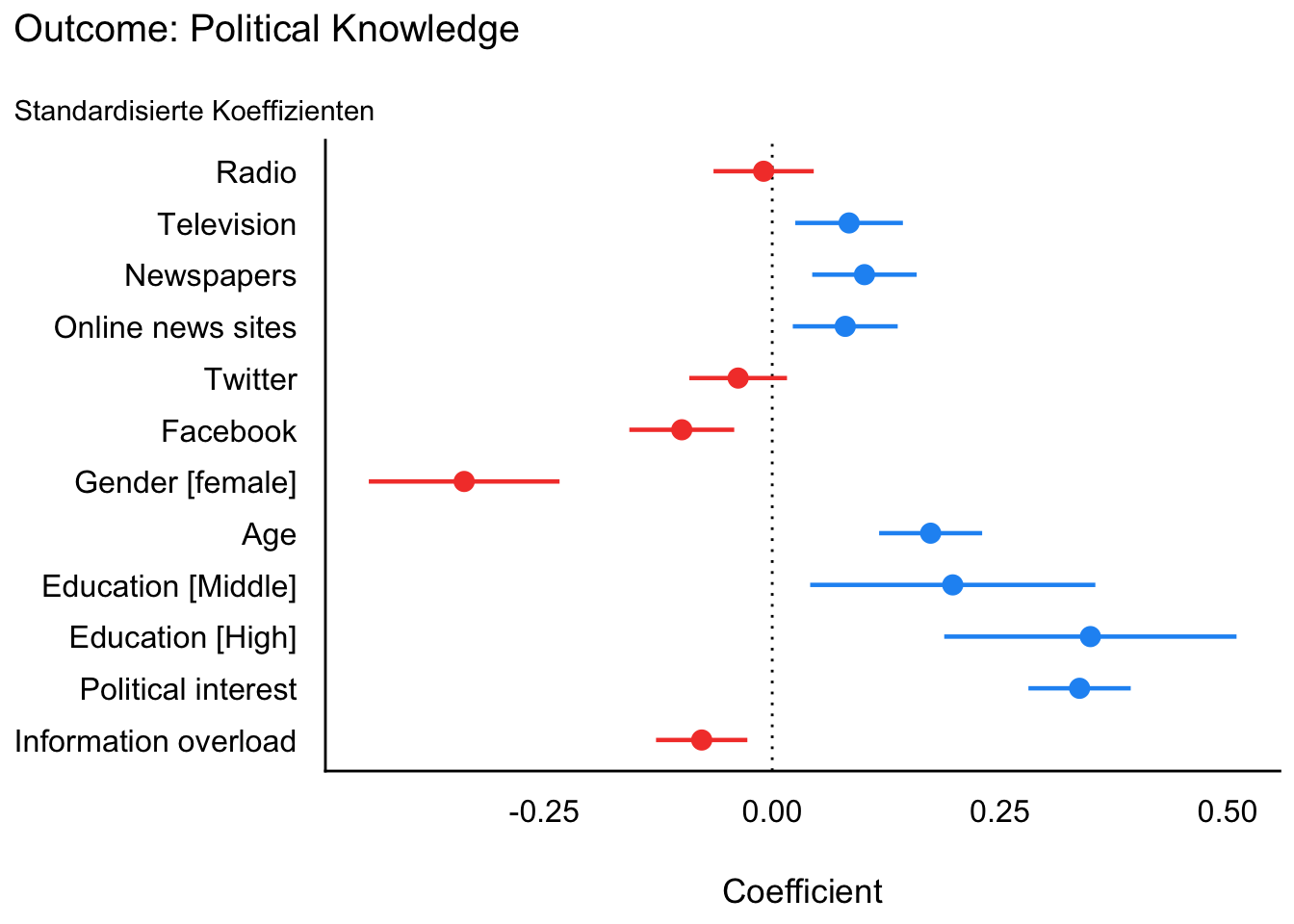
Koeffizientenplot mit standardisierten Koeffizienten

m4 |>
  parameters(standardize = "refit") |>
  plot() +
  ggtitle("Outcome: Political Knowledge",
    subtitle = "Standardisierte Koeffizienten"
  )

Vorhersage fuer einzelne Praediktoren Plot

theme_set(theme_classic(base_size = 12)) # Layout für Plot
m4 |>
  plot_predictions(
    by = "Facebook",
    newdata = datagrid(
      Facebook = 1:6,
      grid_type = "mean_or_mode", # Werte der anderen Prädiktoren
      FUN_integer = mean
    )
  ) # Notwendig, da sonst für Integer Prädiktoren (keine Nachkommastellen) der Modus ausgewählt wird.

Vorhersage für einzelne Praediktoren Tabelle

m4 |>
  predictions(newdata = datagrid(
    Facebook = 1:6,
    grid_type = "mean_or_mode", # Werte der anderen Prädiktoren
    FUN_integer = mean
  )) # Notwendig, da sonst für Integer Prädiktoren (keine Nachkommastellen) der Modus ausgewählt wird.


 Facebook Estimate Std. Error    z Pr(>|z|)      S 2.5 % 97.5 %
        1     3.53     0.0687 51.4   <0.001    Inf  3.40   3.66
        2     3.46     0.0640 54.1   <0.001    Inf  3.34   3.59
        3     3.39     0.0657 51.6   <0.001    Inf  3.26   3.52
        4     3.32     0.0734 45.2   <0.001    Inf  3.18   3.47
        5     3.25     0.0855 38.1   <0.001 1050.3  3.08   3.42
        6     3.18     0.1003 31.7   <0.001  731.9  2.99   3.38

Type: response

theme_set(theme_classic(base_size = 12)) # Layout für Plot
m4 |>
  avg_comparisons(variables = list(
    Facebook = "2sd", Newspapers = "2sd",
    Gender = "reference",
    Education = "pairwise"
  ))


       Term            Contrast Estimate Std. Error     z Pr(>|z|)    S   2.5 %
 Education  High - Lower           0.476     0.1114  4.27  < 0.001 15.7  0.2575
 Education  High - Middle          0.206     0.0757  2.72  0.00654  7.3  0.0575
 Education  Middle - Lower         0.270     0.1086  2.48  0.01297  6.3  0.0570
 Facebook   (x + sd) - (x - sd)   -0.270     0.0799 -3.38  < 0.001 10.5 -0.4271
 Gender     female - male         -0.461     0.0727 -6.34  < 0.001 32.0 -0.6030
 Newspapers (x + sd) - (x - sd)    0.276     0.0796  3.46  < 0.001 10.9  0.1198
 97.5 %
  0.694
  0.354
  0.483
 -0.114
 -0.318
  0.432

Type: response

Ueberpruefung von Linearitaet Normalverteilung Homoskedastizitaet Ausreisser Multikollinearitaet einem Befehl

check_model(m4, check = c("linearity", "normality", "homogeneity", "outliers", "vif"))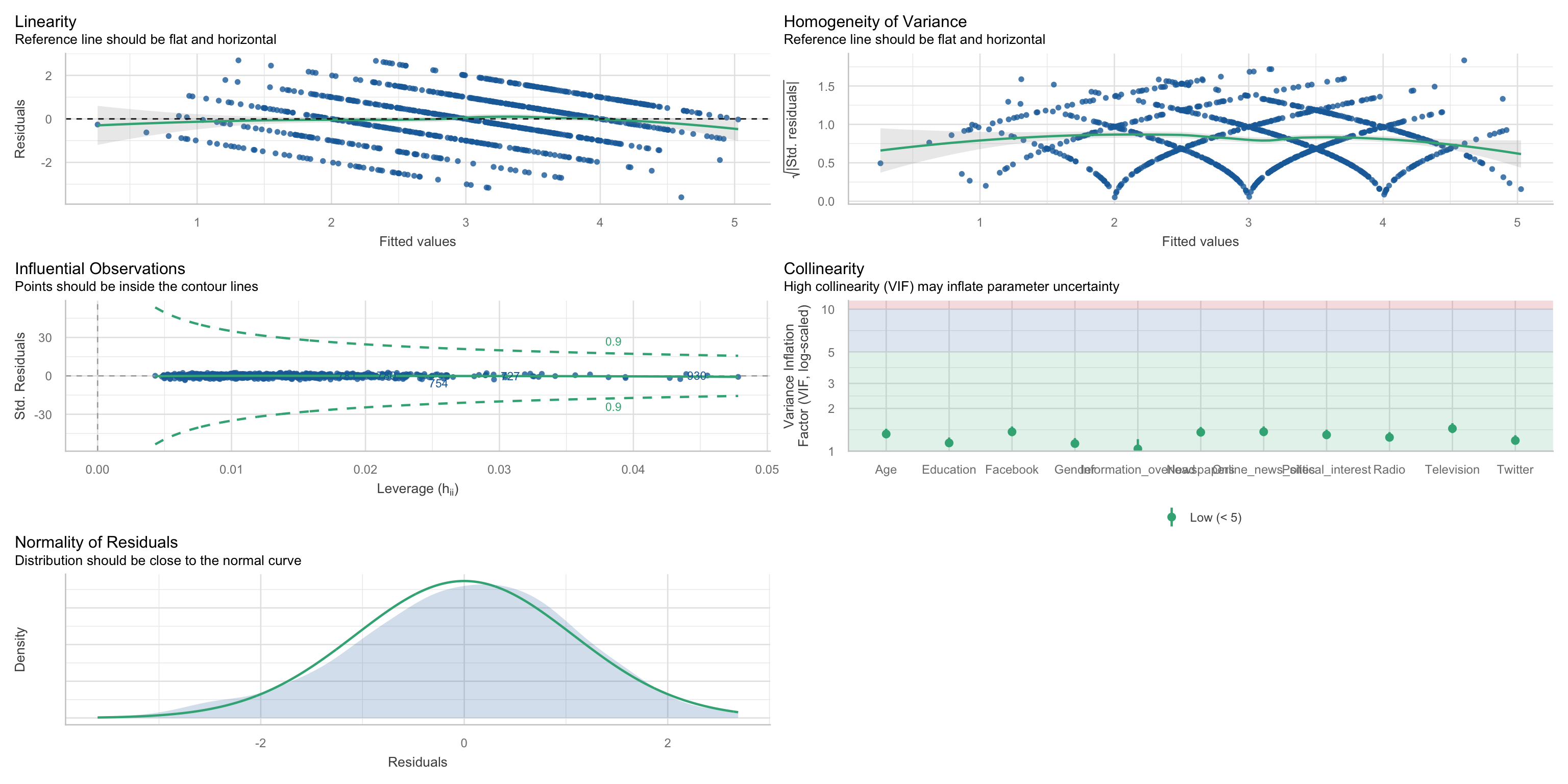

Ueberpruefung Linearitaet

check_model(m4, check = "linearity", panel = FALSE) |> plot()

$NCV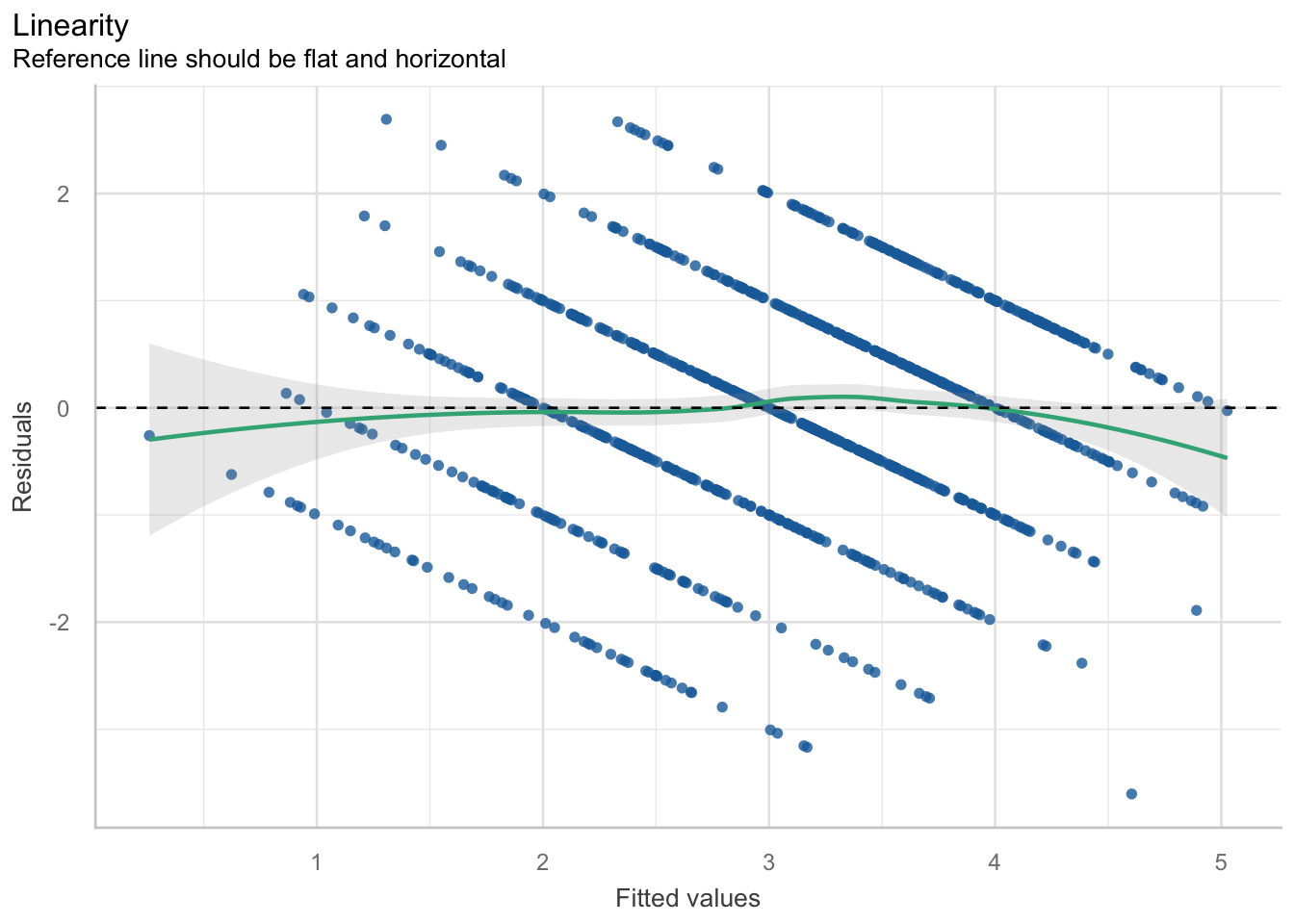

Ueberpruefung Normalverteilung Homoskedastizitaet

check_model(m4, check = c("normality", "homogeneity"))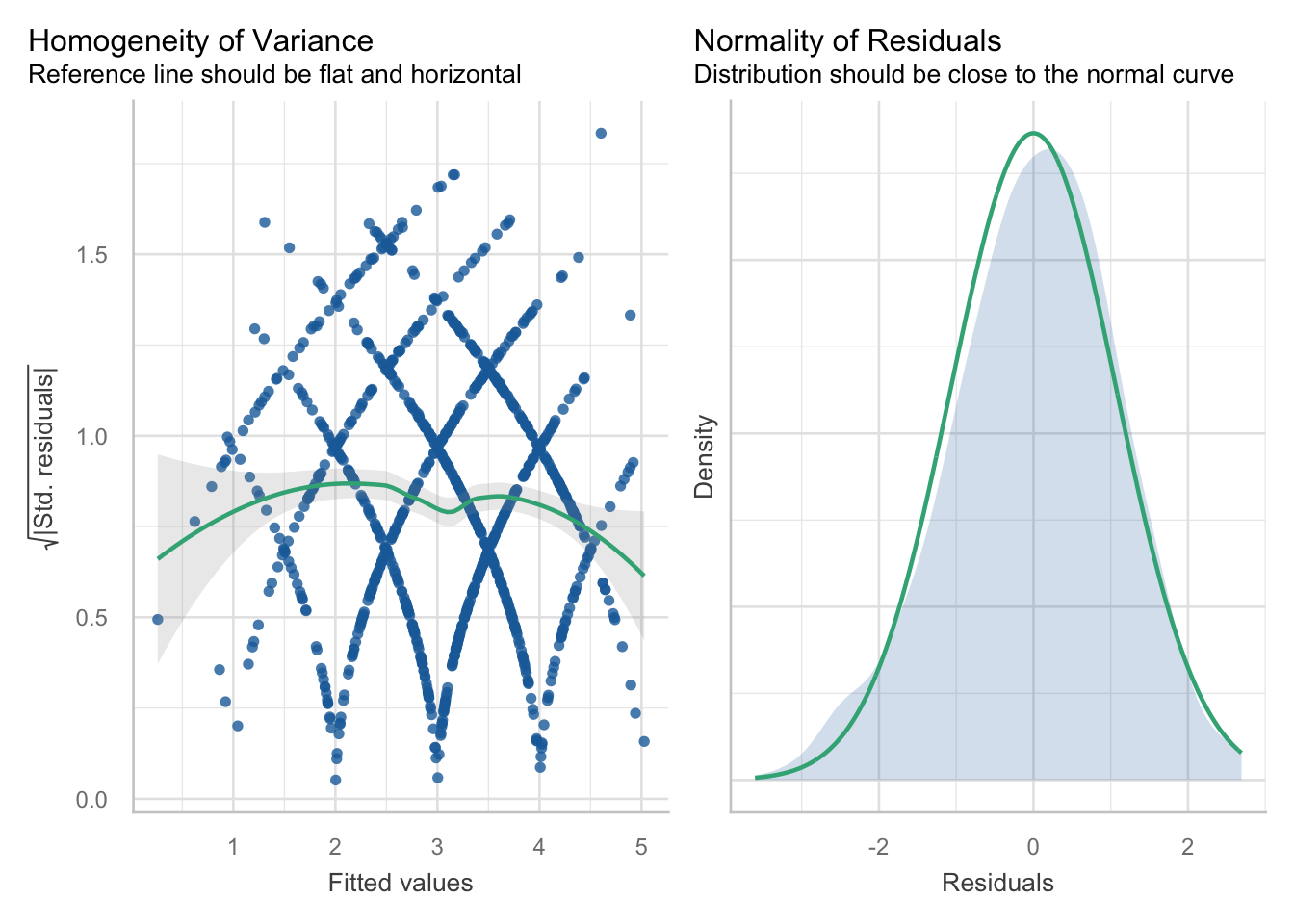

Ueberpruefung Unabhaengigkeit der Residuen

check_residuals(m4) |> plot()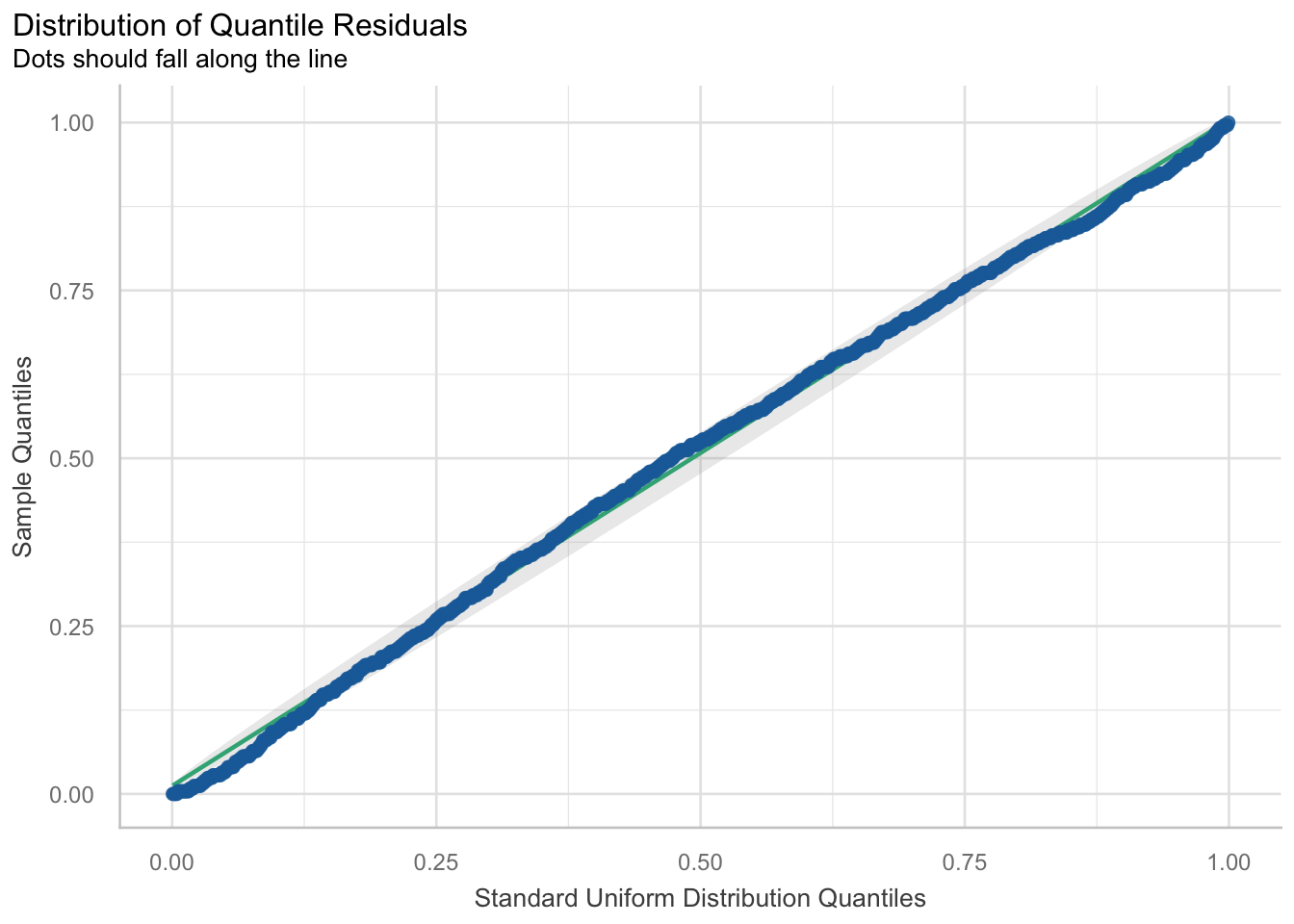

Ueberpruefung Ausreisser

check_outliers(m4) |> plot()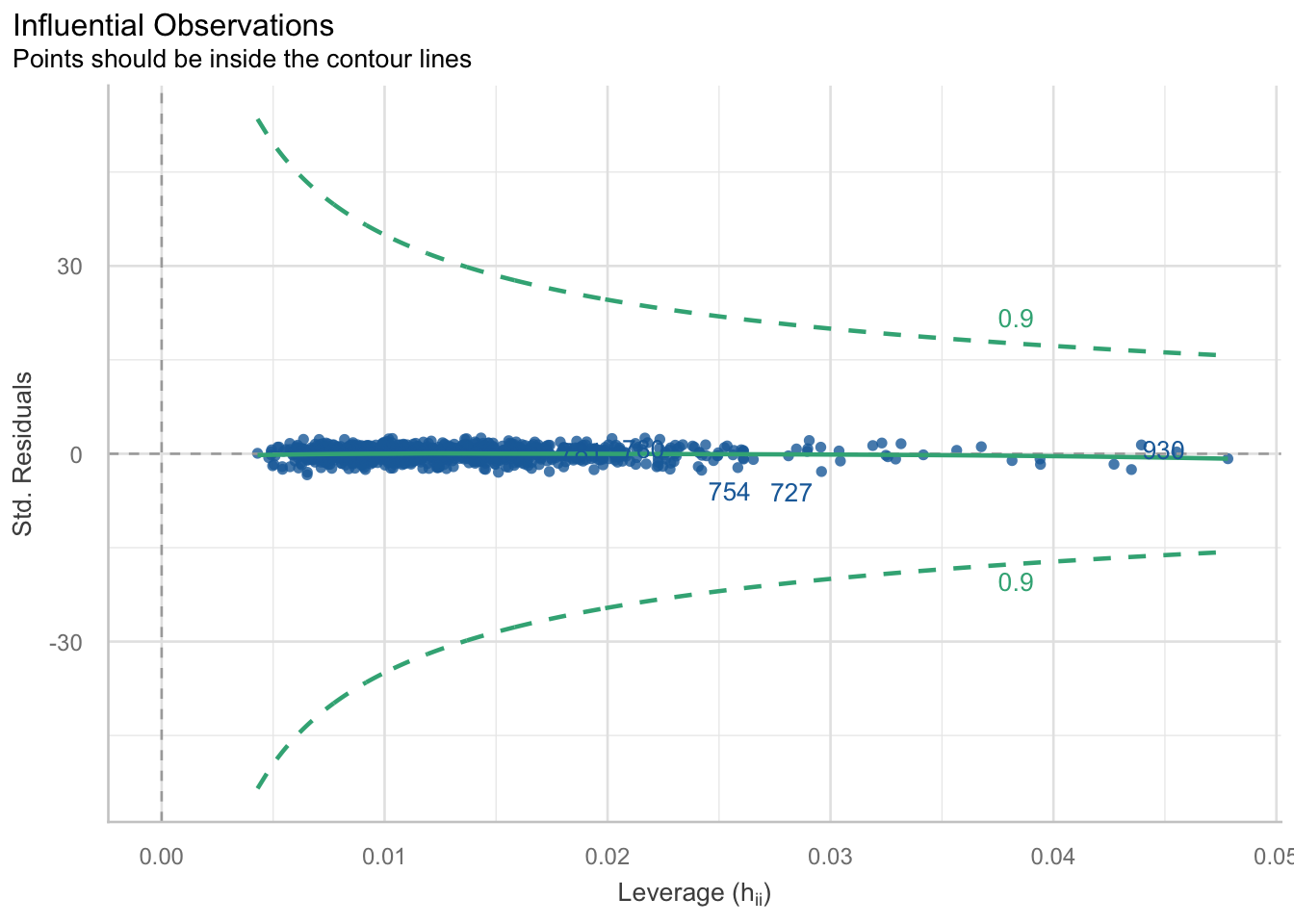

Ueberpruefung Korrelation der Praediktoren

correlation::correlation(m4$model) |> summary(redundant = TRUE)

# Correlation Matrix (pearson-method)

Parameter            | Political_knowledge |   Radio | Television | Newspapers
------------------------------------------------------------------------------
Political_knowledge  |                     | 0.14*** |    0.26*** |    0.33***
Radio                |             0.14*** |         |    0.39*** |    0.28***
Television           |             0.26*** | 0.39*** |            |    0.31***
Newspapers           |             0.33*** | 0.28*** |    0.31*** |           
Online_news_sites    |             0.22*** | 0.22*** |    0.28*** |    0.33***
Twitter              |               -0.04 |    0.09 |       0.04 |       0.09
Facebook             |            -0.13*** | 0.18*** |    0.19*** |       0.06
Age                  |             0.30*** |    0.05 |    0.24*** |    0.21***
Political_interest   |             0.49*** | 0.20*** |    0.30*** |    0.33***
Information_overload |              -0.09* |    0.05 |       0.08 |       0.02

Parameter            | Online_news_sites |  Twitter | Facebook |      Age
-------------------------------------------------------------------------
Political_knowledge  |           0.22*** |    -0.04 | -0.13*** |  0.30***
Radio                |           0.22*** |     0.09 |  0.18*** |     0.05
Television           |           0.28*** |     0.04 |  0.19*** |  0.24***
Newspapers           |           0.33*** |     0.09 |     0.06 |  0.21***
Online_news_sites    |                   |  0.23*** |  0.27*** |    -0.08
Twitter              |           0.23*** |          |  0.33*** | -0.15***
Facebook             |           0.27*** |  0.33*** |          | -0.25***
Age                  |             -0.08 | -0.15*** | -0.25*** |         
Political_interest   |           0.32*** |     0.05 |     0.06 |  0.14***
Information_overload |              0.04 |     0.09 |   0.12** |     0.05

Parameter            | Political_interest | Information_overload
----------------------------------------------------------------
Political_knowledge  |            0.49*** |               -0.09*
Radio                |            0.20*** |                 0.05
Television           |            0.30*** |                 0.08
Newspapers           |            0.33*** |                 0.02
Online_news_sites    |            0.32*** |                 0.04
Twitter              |               0.05 |                 0.09
Facebook             |               0.06 |               0.12**
Age                  |            0.14*** |                 0.05
Political_interest   |                    |                -0.02
Information_overload |              -0.02 |                     

p-value adjustment method: Holm (1979)

Ueberpruefung Multikollinearitaet

check_model(m4, check = "vif", panel = FALSE) |> plot()

$VIF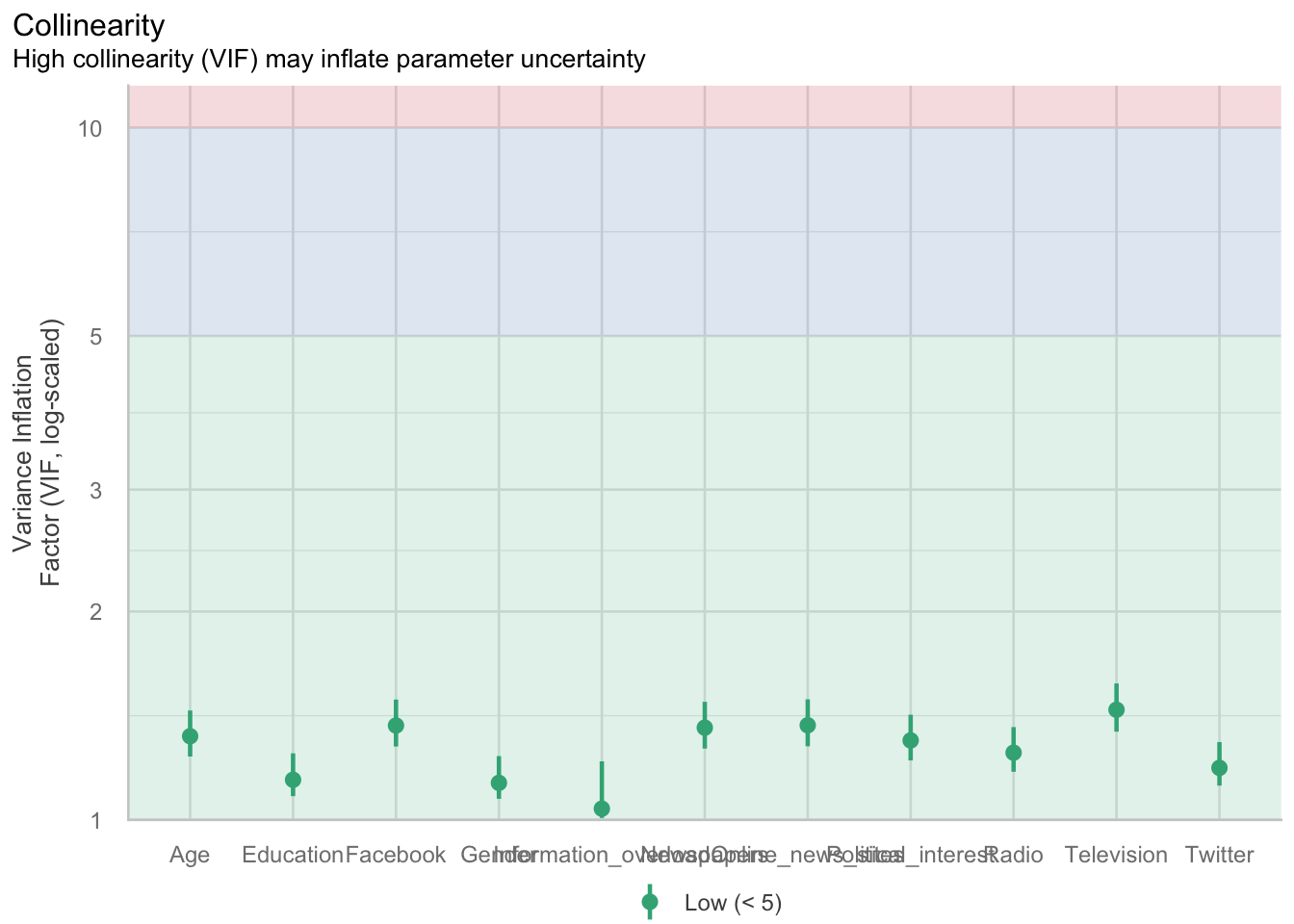

7.4 Hausaufgabe

1) Vollziehen Sie die Analysen nach, deren Ausgaben wir in der Vorlesung besprochen haben.

Schreiben Sie kurze Ergebnistexte zur Beantwortung der Fragen bzw. zum Test der Hypothesen:
- Wie hängen die TV- und Radionutzung mit dem politischen Wissen zusammen?
- Personen, die Twitter häufiger nutzen, beantworten mehr Fragen korrekt.
- Personen, die Facebook häufiger nutzen, beantworten weniger Fragen korrekt.

2) Vollziehen Sie die Analysen nach, die im Artikel in Tabellen 5 und 6 dargestellt sind.

Wie lässt sich die wahrgenommene Personalisierung der eigenen Nachrichtenumgebung erklären?
Wie lässt sich die wahrgenommene Informationsüberlastung erklären?
BONUS: Überprüfen Sie, inwiefern das Modell die statistischen Annahmen erfüllt.

Lösung

Zu 1) Siehe Code und Ausgaben aus der Vorlesung
Zu 2) R Skript | HTML mit Output

7.5 Transkript

Hinweise zum automatisiert erstellten Transkript

Das folgende Transkript wurde auf Basis der Aufzeichnung der Vorlesung erstellt. Die vollständige Aufzeichnungen inklusive der Bildschirminhalte sind in Blackboard🔒 verfügbar. Die Tonspur wurde mit VoiceAI transkribiert. Das Transkript wurde dann mit Sprachmodellen (v.a. Claude Sonnet 4.5) geglättet und formatiert. In diesem Prozess kann es an verschiedenen Stellen zu Fehlern kommen. Im Zweifel gilt das gesprochene Wort, und auch beim Vortrag mache ich Fehler.

Ich stelle das Transkript hier als experimentelles, ergänzendes Material zur Dokumentation der Vorlesung zur Verfügung. Noch bin ich mir unsicher, ob es eine sinnvolle Ergänzung ist und behalte mir vor, es weiter zu bearbeiten oder zu löschen.