6 Wiederholung: Bivariate lineare Regression
6.1 Folien
6.2 Daten der heutigen Sitzung
6.3 Code und Ausgaben aus der Vorlesung
Laden der relevanten Pakete
library(report) # Einfaches Erstellen von statistischen Berichten
library(marginaleffects) # Vorhersagen aus Regressionsmodellen
library(performance) # Prüfen der Voraussetzungen
library(tidyverse) # Datenmanagement und Visualisierung: https://www.tidyverse.org/── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.6
✔ forcats 1.0.1 ✔ stringr 1.6.0
✔ ggplot2 4.0.1 ✔ tibble 3.3.0
✔ lubridate 1.9.4 ✔ tidyr 1.3.1
✔ purrr 1.2.0
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsLesen und Aufbereiten des Datensatz von Van Erkel & Van Aelst
d <- haven::read_stata(here::here("data/Vanerkel_Vanaelst_2021.dta")) |>
rename(
Political_knowledge = PK,
Personalized_news = personalized_news,
Radio = News_channels_w4_1,
Television = News_channels_w4_2,
Newspapers = News_channels_w4_3,
Online_news_sites = News_channels_w4_4,
Twitter = News_channels_w4_5,
Facebook = News_channels_w4_6
) |>
mutate(
Gender = as_factor(Gender),
Education = as_factor(Education),
trad = factor(trad, labels = c(
"traditional news diet: no",
"traditional news diet: yes"
))
)Scatterplot
d |>
ggplot(aes(Age, Political_knowledge)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE, linewidth = 2) +
xlim(c(18, 72)) +
scale_y_continuous(breaks = 0:5, limits = c(-0.3, 5.3)) +
theme_classic(base_size = 12)`geom_smooth()` using formula = 'y ~ x'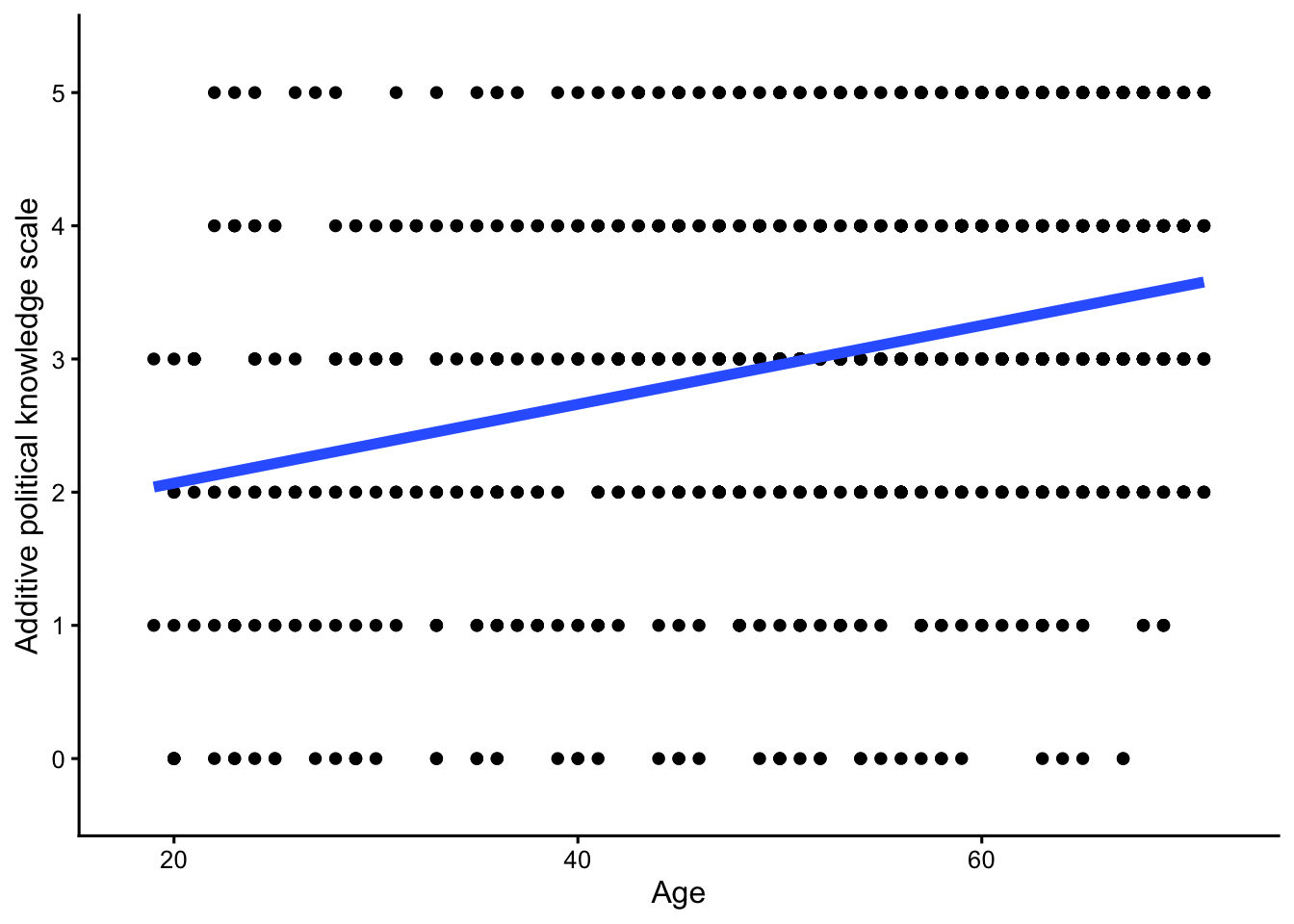
Jittered scatterplot
jit_scat <- d |>
ggplot(aes(Age, Political_knowledge)) +
geom_jitter(width = 0.3, height = 0.3) +
geom_smooth(method = "lm", se = FALSE, linewidth = 2) +
xlim(c(18, 72)) +
scale_y_continuous(breaks = 0:5, limits = c(-0.3, 5.3)) +
theme_classic(base_size = 12)
jit_scat`geom_smooth()` using formula = 'y ~ x'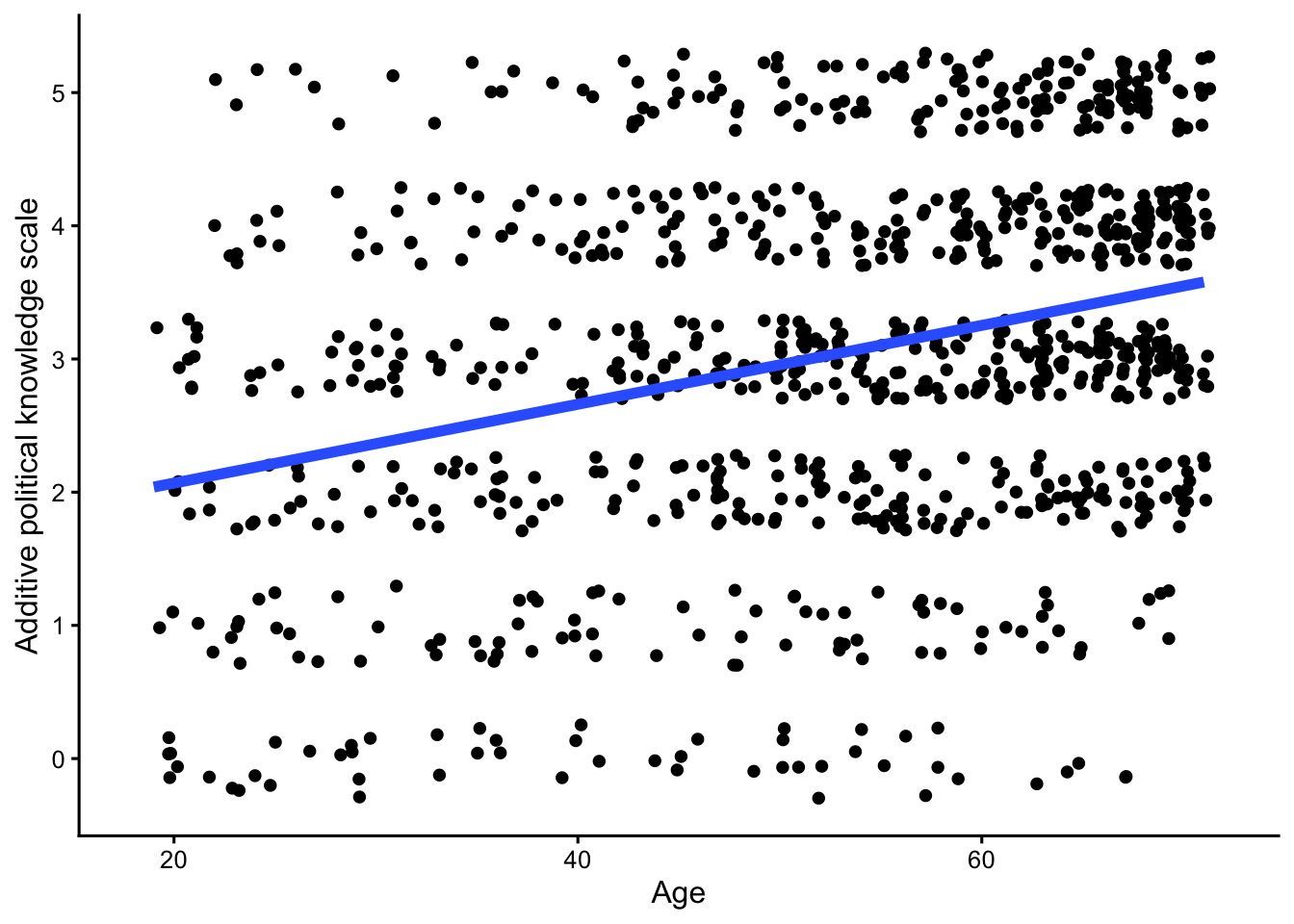
Regression Politisches Wissen und Alter schätzen
m_pk_age <- lm(Political_knowledge ~ Age, data = d)
m_pk_age
Call:
lm(formula = Political_knowledge ~ Age, data = d)
Coefficients:
(Intercept) Age
1.4761 0.0296 Regression mit Z-standardisierten Variablen zum Vergleich mit Korrelationskoeffizienten
lm(scale(Political_knowledge) ~ scale(Age), data = d)
Call:
lm(formula = scale(Political_knowledge) ~ scale(Age), data = d)
Coefficients:
(Intercept) scale(Age)
8.080e-17 3.034e-01 Korrelation
cor(d$Political_knowledge, d$Age)[1] 0.3033832Regressionstabelle mit Inferenzstatistik
lm(Political_knowledge ~ Age, data = d) |>
report_table(metrics = "R2")Parameter | Coefficient | 95% CI | t(991) | p | Std. Coef.
-----------------------------------------------------------------------
(Intercept) | 1.48 | [1.16, 1.79] | 9.12 | < .001 | 3.46e-16
Age | 0.03 | [0.02, 0.04] | 10.02 | < .001 | 0.30
| | | | |
R2 | | | | |
Parameter | Std. Coef. 95% CI | Fit
--------------------------------------
(Intercept) | [-0.06, 0.06] |
Age | [ 0.24, 0.36] |
| |
R2 | | 0.09Korrelationskoeffizient mit Inferenzstatistik
cor.test(~ Political_knowledge + Age, data = d) |>
report_statistics()In the report() function, for htest objects, you can try providing the
data argument manually, e.g., report(x, data = data).r = 0.30, 95% CI [0.25, 0.36], t(991) = 10.02, p < .001
Vorhersagen Tabelle
m_pk_age |>
avg_predictions(variables = list(Age = "threenum")) # "threenum" = Vorhersage für M-SD, M, M+SD
Age Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
39.0 2.63 0.0583 45.1 <0.001 Inf 2.52 2.75
53.0 3.04 0.0412 73.9 <0.001 Inf 2.96 3.13
66.9 3.46 0.0583 59.3 <0.001 Inf 3.34 3.57
Type: responseVorhersagen Plot
theme_set(theme_classic(base_size = 12)) # Layout für Plot
m_pk_age |>
plot_predictions(condition = list(Age = "threenum"))
Regression mit binärem Prädiktor Gender
lm(Political_knowledge ~ Gender, data = d) |>
report_table(include_effectsize = FALSE, metrics = "R2")Parameter | Coefficient | 95% CI | t(991) | p | Fit
-----------------------------------------------------------------------
(Intercept) | 3.44 | [ 3.33, 3.55] | 60.48 | < .001 |
Gender [female] | -0.84 | [-1.00, -0.67] | -10.14 | < .001 |
| | | | |
R2 | | | | | 0.09T-Test zum Gruppenvergleich nach Gender
t.test(Political_knowledge ~ Gender, data = d, var.equal = FALSE) |>
report_table(data = d)Welch Two Sample t-test
Parameter | Group | Mean_Group1 | Mean_Group2 | Difference
---------------------------------------------------------------------
Political_knowledge | Gender | 3.44 | 2.61 | 0.84
Parameter | 95% CI | t(987.31) | p | Cohen's d | Cohen's d CI
-----------------------------------------------------------------------------------
Political_knowledge | [0.67, 1.00] | 10.15 | < .001 | 0.64 | [0.52, 0.77]
Alternative hypothesis: two.sidedUeberpruefung von Linearitaet Normalverteilung Homoskedastizitaet Ausreisser in einem Befehl
check_model(m_pk_age, check = c("linearity", "normality", "homogeneity", "outliers"))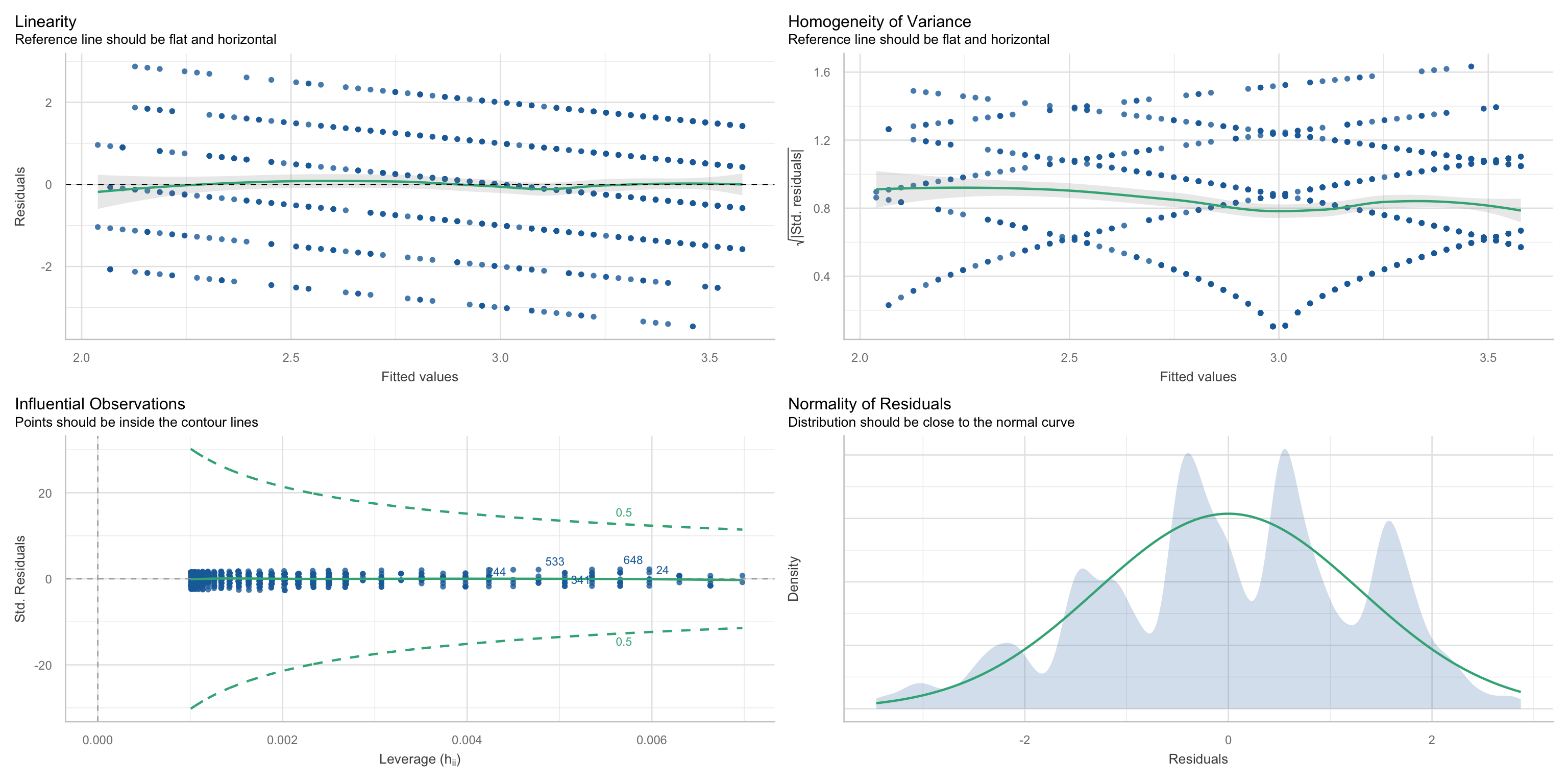
Ueberpruefung Linearitaet
check_model(m_pk_age, check = "linearity", panel = FALSE) |> plot()$NCV
Ueberpruefung Normalverteilung Homoskedastizitaet
check_model(m_pk_age, check = c("normality", "homogeneity"))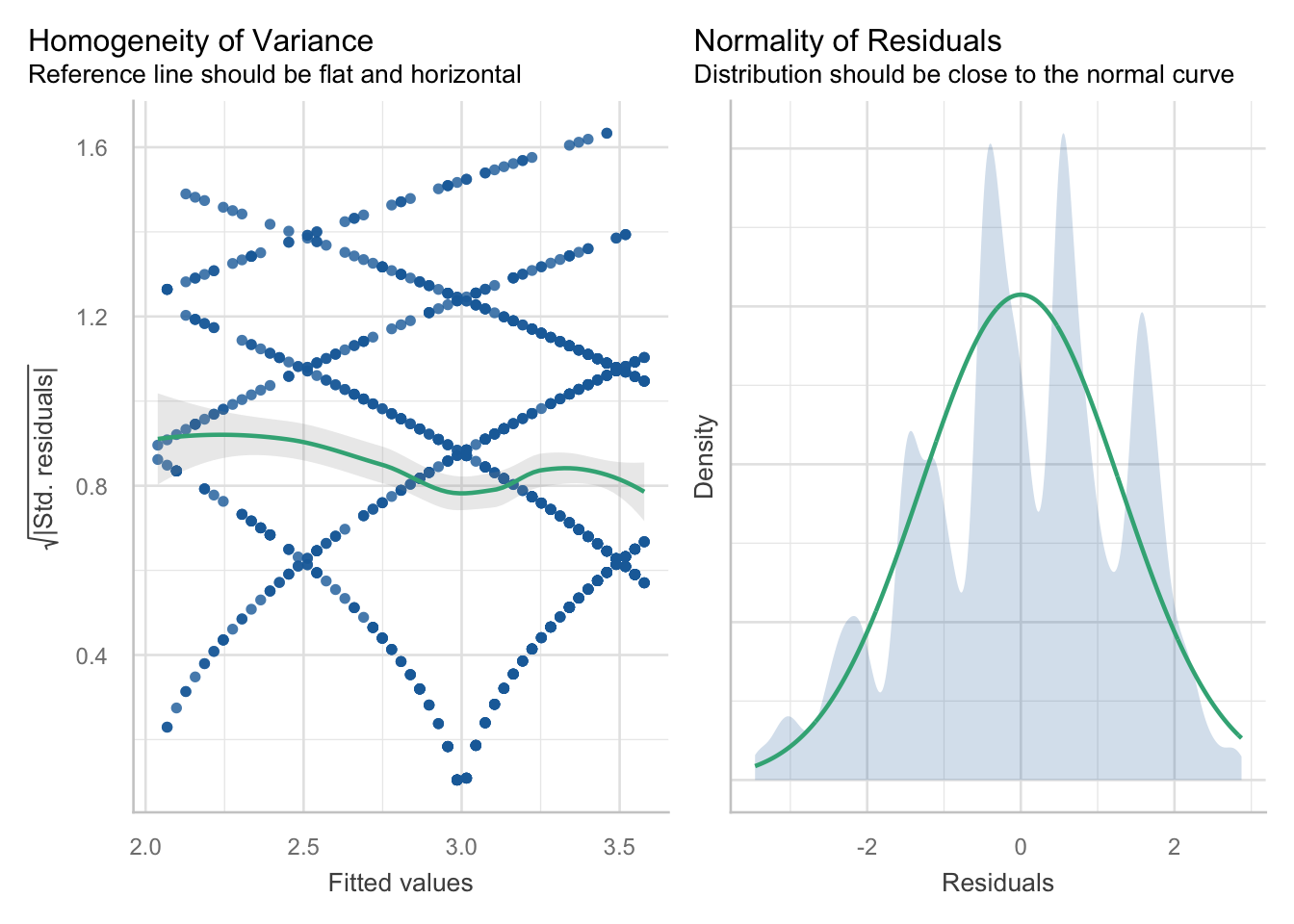
Ueberpruefung Unabhaengigkeit der Residuen
check_residuals(m_pk_age) |> plot()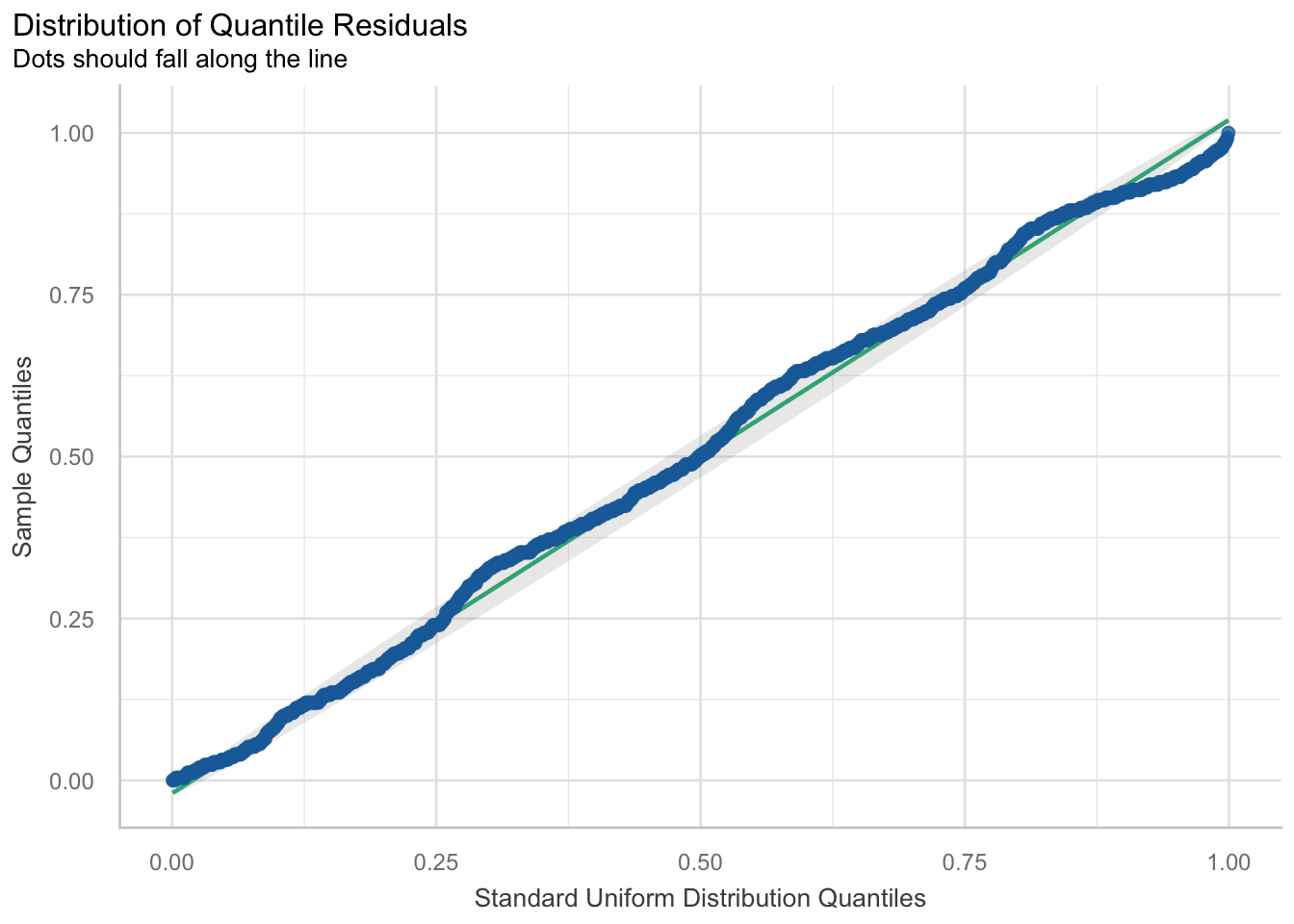
Ueberpruefung Ausreisser
check_outliers(m_pk_age) |> plot()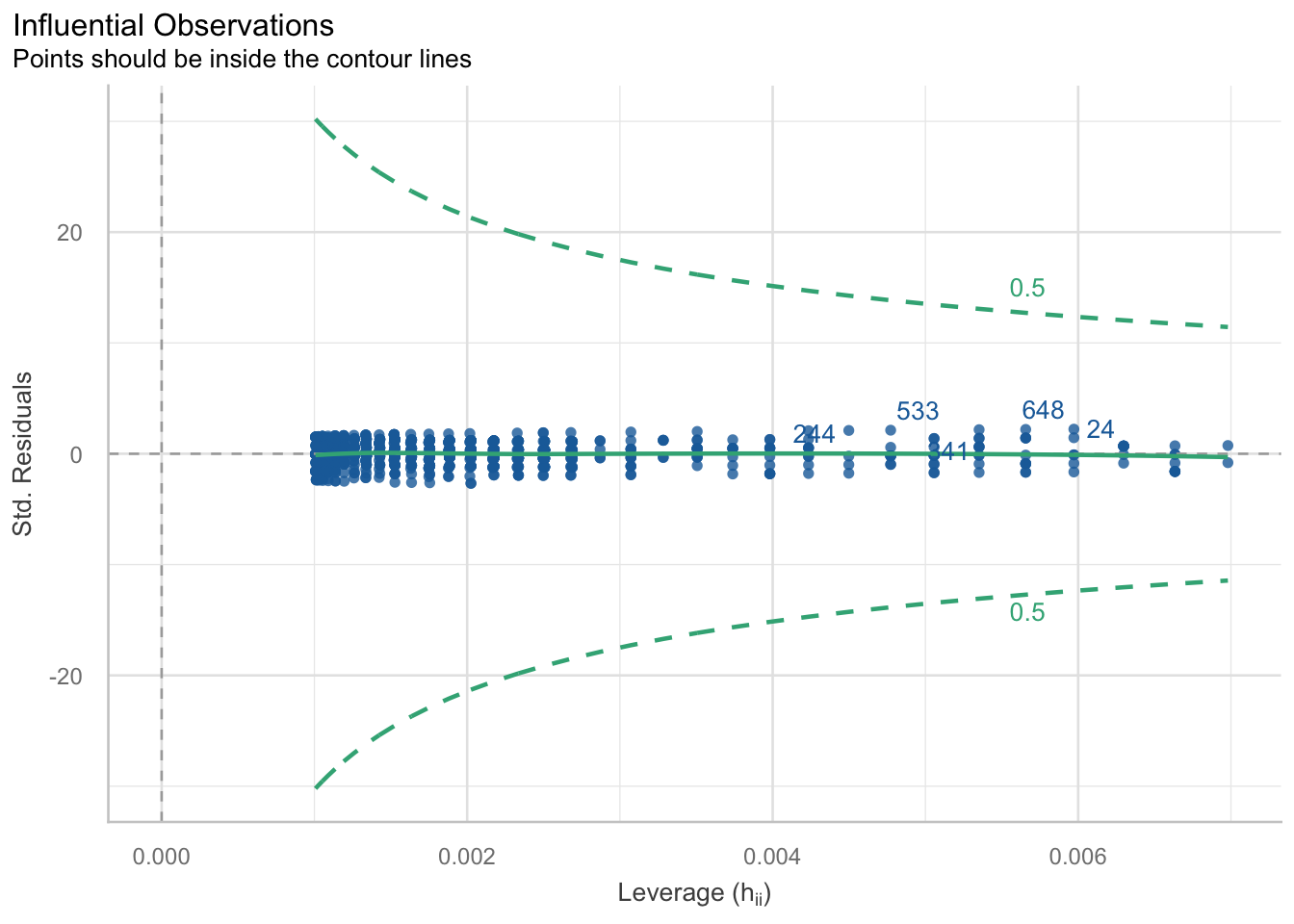
Zentrieren um Mittelwert
d <- d |>
mutate(Age_c = Age - mean(Age))Zentrieren um Mittelwert Plot
theme_set(theme_classic(base_size = 12))
d |>
ggplot(aes(Age, Age_c)) +
geom_point()
Regression Original zum Vergleich
m_pk_age |>
report_table(metrics = "R2", include_effectsize = FALSE)Parameter | Coefficient | 95% CI | t(991) | p | Fit
-----------------------------------------------------------------
(Intercept) | 1.48 | [1.16, 1.79] | 9.12 | < .001 |
Age | 0.03 | [0.02, 0.04] | 10.02 | < .001 |
| | | | |
R2 | | | | | 0.09Regression mit zentriertem Prädiktor
lm(Political_knowledge ~ Age_c, data = d) |>
report_table(metrics = "R2", include_effectsize = FALSE)Parameter | Coefficient | 95% CI | t(991) | p | Fit
-----------------------------------------------------------------
(Intercept) | 3.04 | [2.96, 3.13] | 73.88 | < .001 |
Age c | 0.03 | [0.02, 0.04] | 10.02 | < .001 |
| | | | |
R2 | | | | | 0.09Alter in 10-Jahres-Schritten
d <- d |>
mutate(Age_10 = Age / 10)Alter in 10-Jahres-Schritten Plot
d |>
ggplot(aes(Age, Age_10)) +
geom_point()
Regression mit Alter in 10-Jahres-Schritten als Prädiktor
lm(Political_knowledge ~ Age_10, data = d) |>
report_table(metrics = "R2", include_effectsize = FALSE)Parameter | Coefficient | 95% CI | t(991) | p | Fit
-----------------------------------------------------------------
(Intercept) | 1.48 | [1.16, 1.79] | 9.12 | < .001 |
Age 10 | 0.30 | [0.24, 0.35] | 10.02 | < .001 |
| | | | |
R2 | | | | | 0.09Z-Standardisierung
d <- d |>
mutate(
Age_z = (Age - mean(Age)) / sd(Age),
Political_knowledge_z = scale(Political_knowledge, center = TRUE, scale = TRUE)
)Z-Standardisierung Plot Alter
d |>
ggplot(aes(Age, Age_z)) +
geom_point()
Z-Standardisierung Plot Politisches Wissen
d |>
ggplot(aes(Political_knowledge, Political_knowledge_z)) +
geom_point(size = 8)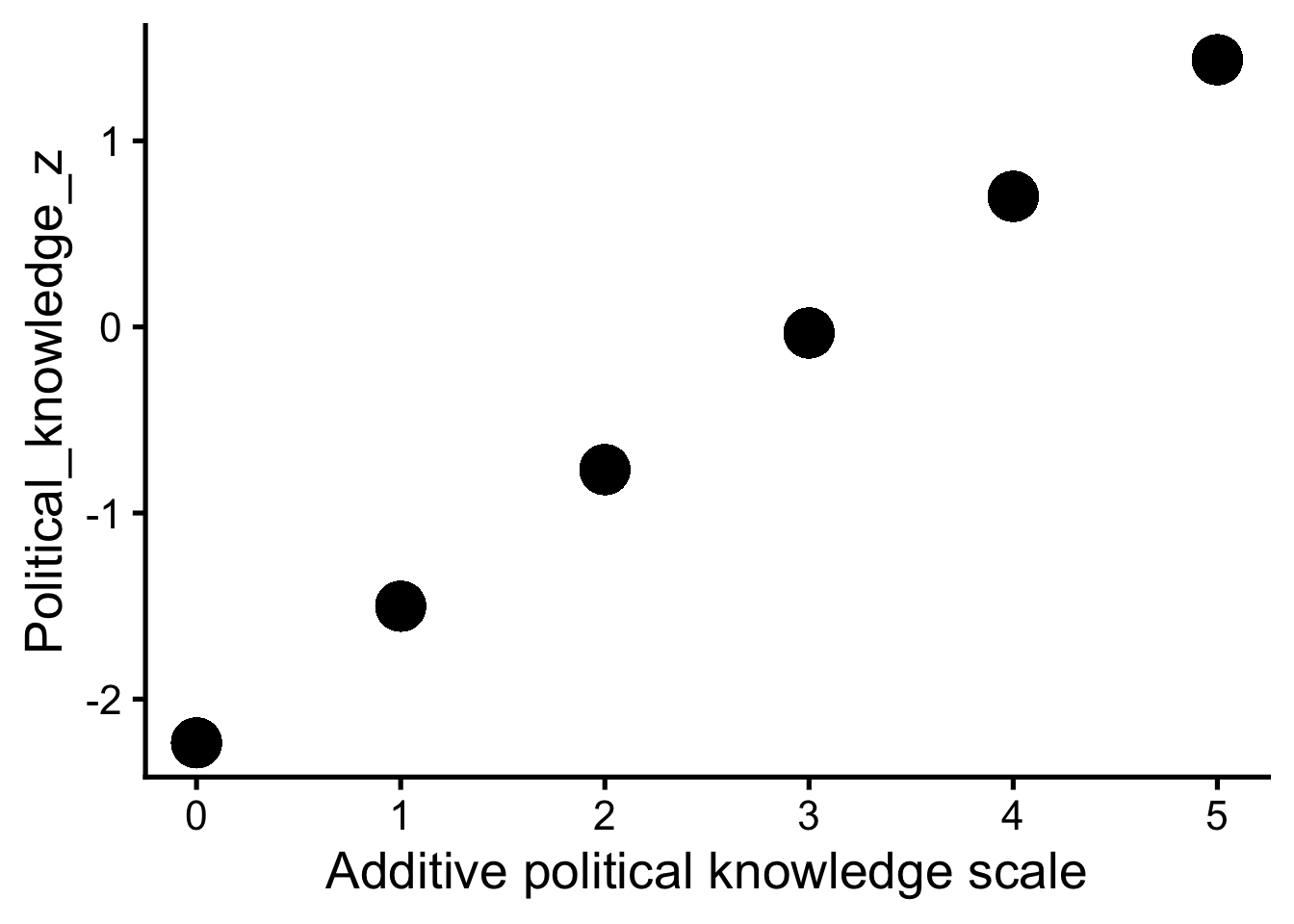
Regression mit Z-standardisierten Variablen
lm(Political_knowledge_z ~ Age_z, data = d) |>
report_table(metrics = "R2", include_effectsize = FALSE)Parameter | Coefficient | 95% CI | t(991) | p | Fit
--------------------------------------------------------------------
(Intercept) | 8.08e-17 | [-0.06, 0.06] | 2.67e-15 | > .999 |
Age z | 0.30 | [ 0.24, 0.36] | 10.02 | < .001 |
| | | | |
R2 | | | | | 0.09Regressionstabelle mit standardisierten Koeffizienten
m_pk_age |>
report_table(metrics = "R2", include_effectsize = TRUE)Parameter | Coefficient | 95% CI | t(991) | p | Std. Coef.
-----------------------------------------------------------------------
(Intercept) | 1.48 | [1.16, 1.79] | 9.12 | < .001 | 3.46e-16
Age | 0.03 | [0.02, 0.04] | 10.02 | < .001 | 0.30
| | | | |
R2 | | | | |
Parameter | Std. Coef. 95% CI | Fit
--------------------------------------
(Intercept) | [-0.06, 0.06] |
Age | [ 0.24, 0.36] |
| |
R2 | | 0.09log-Transformation
d <- d |>
mutate(
Age_log = log(Age),
Political_knowledge_log = log1p(Political_knowledge)
)log-Transformation Plot Age
d |>
ggplot(aes(Age, Age_log)) +
geom_point()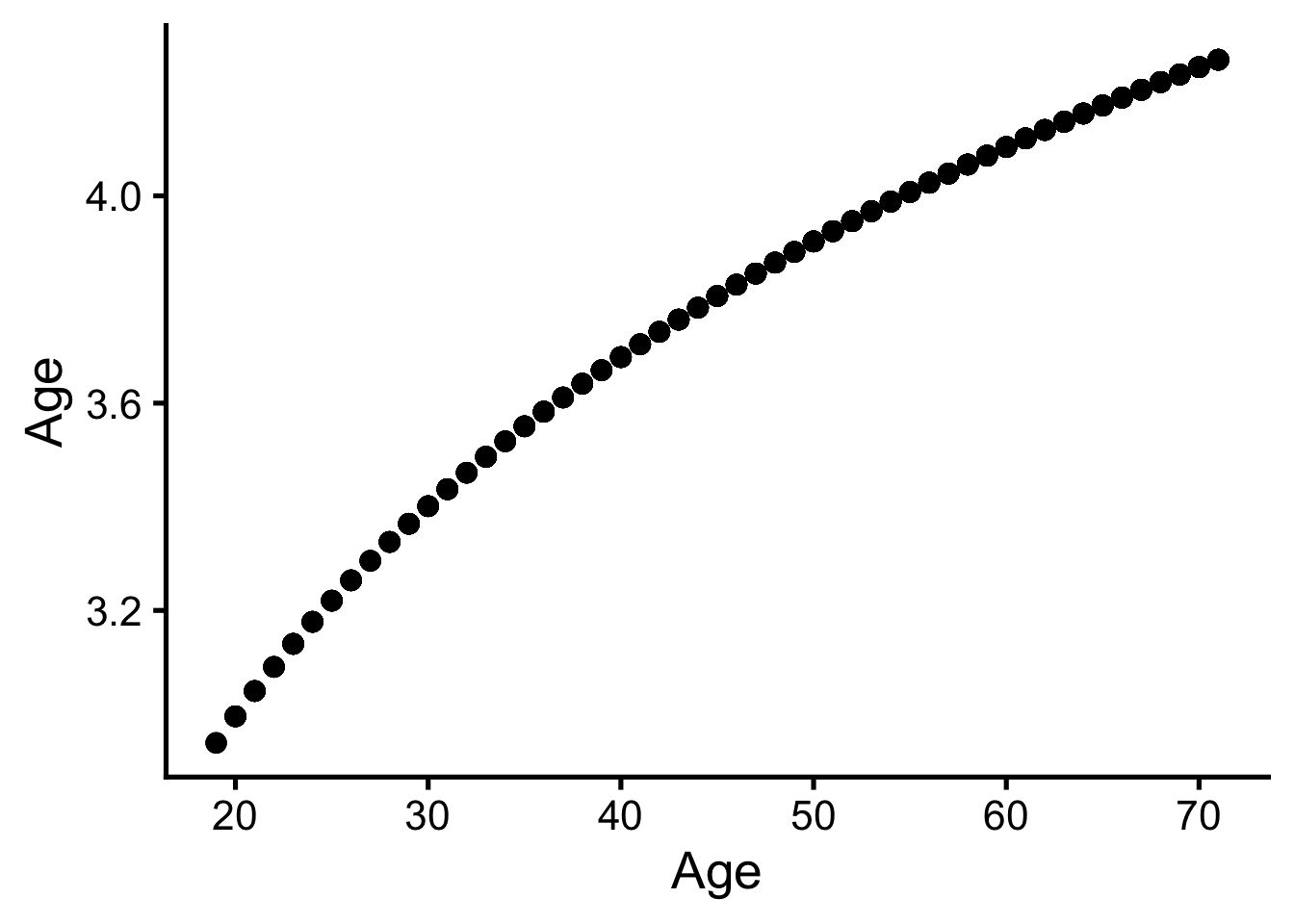
log-Transformation Politisches Wissen
d |>
ggplot(aes(Political_knowledge, Political_knowledge_log)) +
geom_point(size = 8)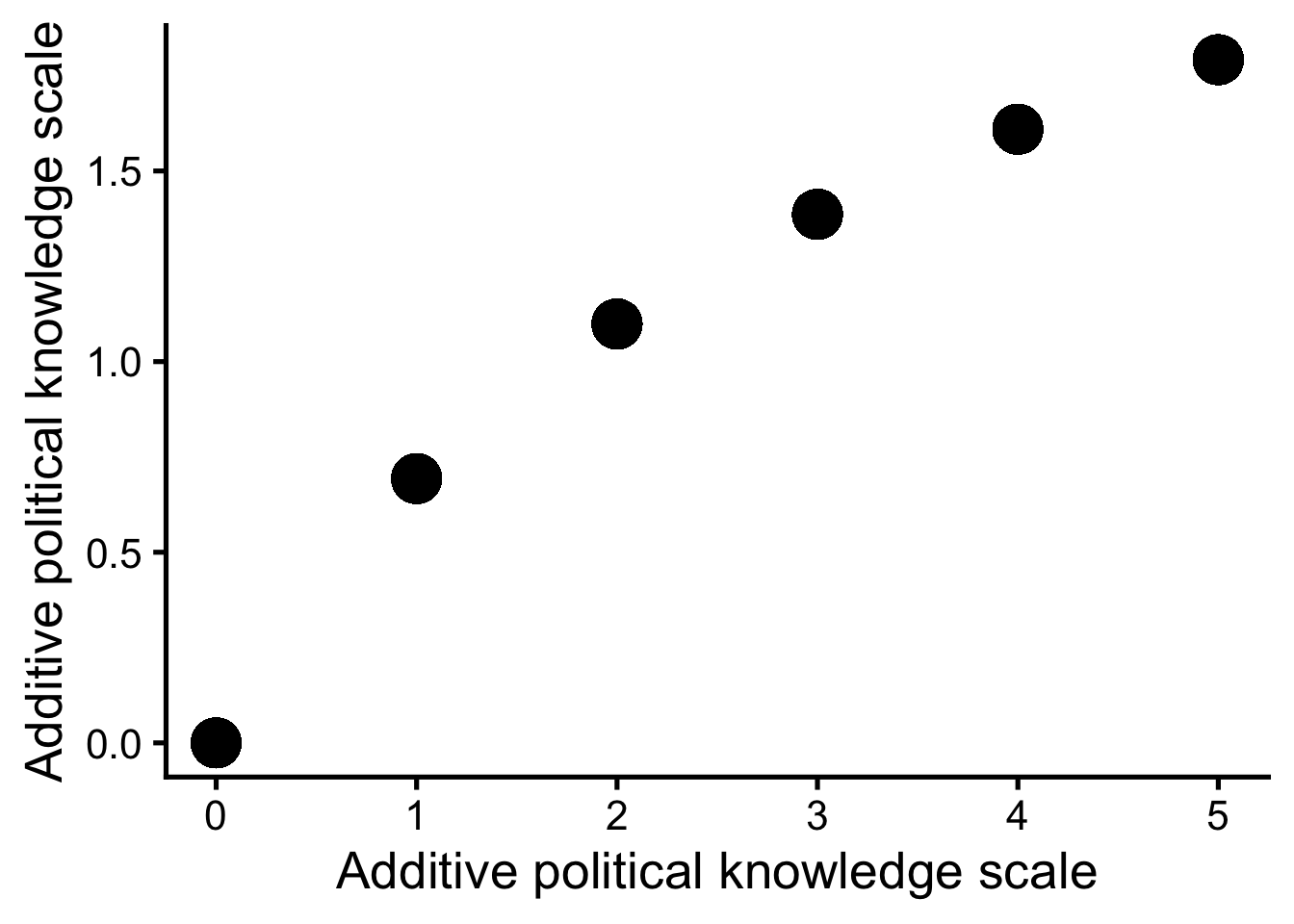
Regression mit log-transformierten Variablen
lm(Political_knowledge_log ~ Age_log, data = d) |>
report_table(metrics = "R2", include_effectsize = FALSE)Parameter | Coefficient | 95% CI | t(991) | p | Fit
-------------------------------------------------------------------
(Intercept) | -0.38 | [-0.70, -0.06] | -2.31 | 0.021 |
Age log | 0.43 | [ 0.35, 0.51] | 10.41 | < .001 |
| | | | |
R2 | | | | | 0.106.4 Hausaufgabe
1) Vollziehen Sie die Analysen nach, deren Ausgaben wir in der Vorlesung besprochen haben.
- Schreiben Sie kurze Ergebnistexte zur Beantwortung der Fragen bzw. zum Test der Hypothesen:
- FF: Wie hängen Alter und politisches Wissen in der Stichprobe zusammen?
- H: Je älter eine Person, desto mehr Wissensfragen beantwortet sie richtig.
- H: Männer wissen mehr über Politik als Frauen.
2) Prüfen Sie die Hypothese: Je häufiger eine Person Zeitungen nutzt, desto höher ist ihr politisches Wissen.
- Zeitungsnutzung: Variable
Newspapers - Stellen Sie den Zusammenhang als ‘jittered Scatterplot’ dar.
- Schätzen Sie den Zusammenhang mit einer linearen Regression.
- Sagen Sie das politische Wissen für Personen mit unterdurchschnittlicher, durchschnittlicher und überdurchschnittlicher Zeitungsnutzung voraus.
- Interpretieren Sie die Ergebnisse. Schreiben Sie dazu einen kurzen Text.
- BONUS: Überprüfen Sie, inwiefern das Modell die statistischen Annahmen erfüllt.
- BONUS: Zentrieren Sie die Variable
Newspapersum ihren Mittelwert. Verwenden Sie die neue VariableNewspapers_zin einer Regressionsanalyse und vergleichen Sie die Ergebnisse.
Lösung
- Zu 1) Siehe Code und Ausgaben aus der Vorlesung
- Zu 2) R Skript | HTML mit Output
6.5 Transkript
Das folgende Transkript wurde auf Basis der Aufzeichnung der Vorlesung erstellt. Die vollständige Aufzeichnungen inklusive der Bildschirminhalte sind in Blackboard🔒 verfügbar. Die Tonspur wurde mit VoiceAI transkribiert. Das Transkript wurde dann mit Sprachmodellen (v.a. Claude Sonnet 4.5) geglättet und formatiert. In diesem Prozess kann es an verschiedenen Stellen zu Fehlern kommen. Im Zweifel gilt das gesprochene Wort, und auch beim Vortrag mache ich Fehler.
Ich stelle das Transkript hier als experimentelles, ergänzendes Material zur Dokumentation der Vorlesung zur Verfügung. Noch bin ich mir unsicher, ob es eine sinnvolle Ergänzung ist und behalte mir vor, es weiter zu bearbeiten oder zu löschen.
