3 Wiederholung: Frequentistische Inferenzstatistik
3.1 Folien
3.2 Daten der heutigen Sitzung
3.3 Code und Ausgaben aus der Vorlesung
Laden der relevanten Pakete
library(report) # Einfaches Erstellen von statistischen Berichten
library(datawizard) # Für Kreuztabellen
library(tidyverse) # Datenmanagement und Visualisierung: https://www.tidyverse.org/── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.6
✔ forcats 1.0.1 ✔ stringr 1.6.0
✔ ggplot2 4.0.1 ✔ tibble 3.3.0
✔ lubridate 1.9.4 ✔ tidyr 1.3.1
✔ purrr 1.2.0
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsLesen und Aufbereiten des Datensatz von Van Erkel & Van Aelst
d <- haven::read_stata(here::here("data/Vanerkel_Vanaelst_2021.dta")) |>
rename(
Political_knowledge = PK,
Personalized_news = personalized_news,
Radio = News_channels_w4_1,
Television = News_channels_w4_2,
Newspapers = News_channels_w4_3,
Online_news_sites = News_channels_w4_4,
Twitter = News_channels_w4_5,
Facebook = News_channels_w4_6
) |>
mutate(
Gender = as_factor(Gender),
Education = as_factor(Education),
trad = factor(trad, labels = c(
"traditional news diet: no",
"traditional news diet: yes"
))
)Simulation der Konfidenzintervalle nur zur Illustration kein Klausurstoff
theme_set(theme_minimal())
set.seed(11)
M_PK <- mean(d$Political_knowledge)
GG <- rpois(6.8e6, lambda = M_PK)
n <- 500
sim <- replicate(100, {
STP <- sample(GG, n, replace = FALSE)
mdl <- lm(STP ~ 1)
cnfs <- confint(mdl)
c(M = unname(coef(mdl)), conf.low = cnfs[1], conf.high = cnfs[2])
}) |>
t() |>
data.frame() |>
arrange(M) |>
mutate(inside = if_else(conf.low > M_PK | conf.high < M_PK, "red", "black"))
sim |>
ggplot(aes(1:100, M, ymin = conf.low, ymax = conf.high, color = inside)) +
geom_pointrange() +
geom_hline(yintercept = M_PK) +
scale_colour_identity() +
scale_x_continuous(name = NULL) +
ggtitle("Mittelwerte und 95%-Konfidenzintervalle von 100 wiederholten Stichproben derselben Grundgesamtheit")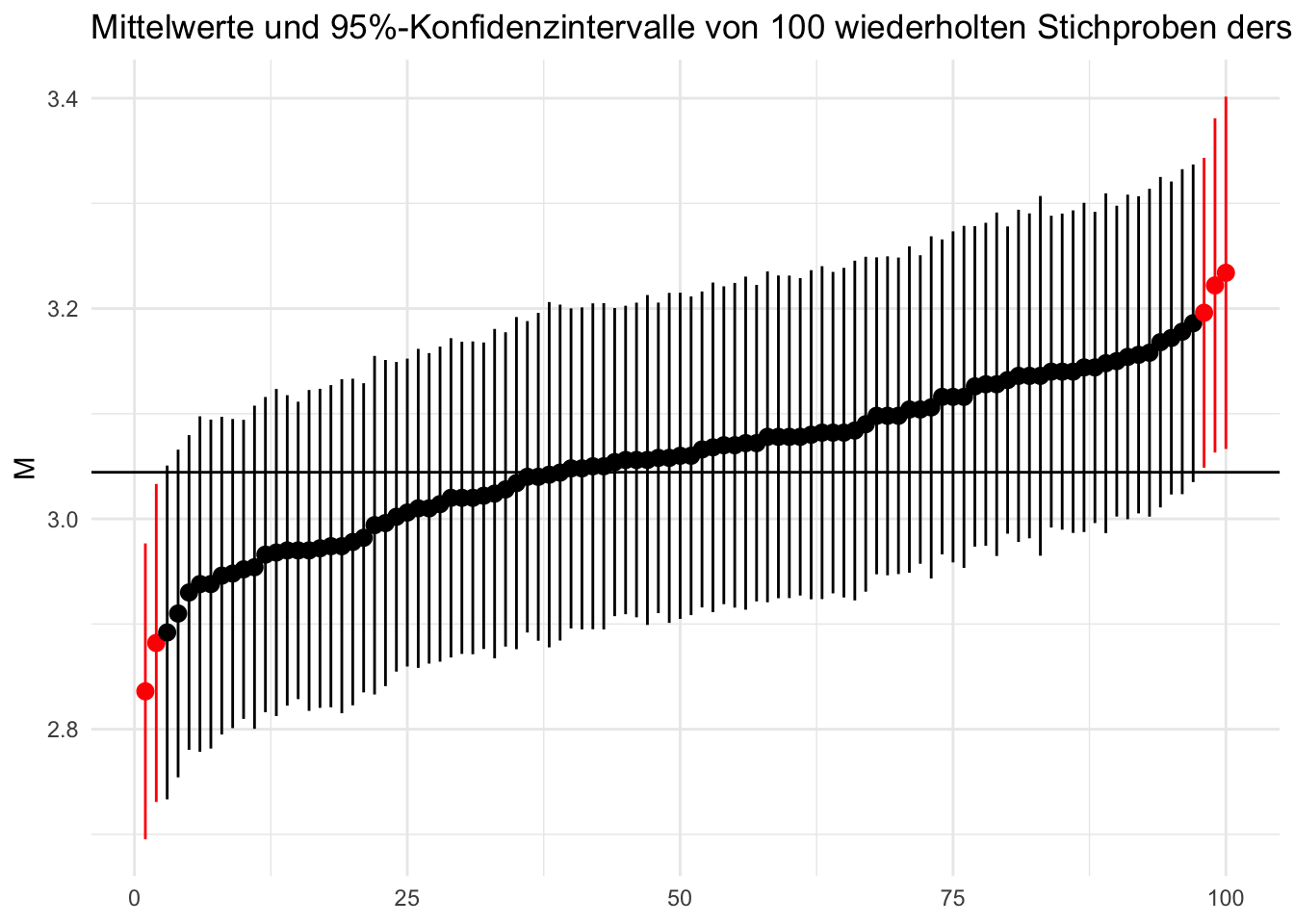
Berechnung des Konfidenzintervalls für einen Mittelwert
d |>
summarize(
M = mean(Political_knowledge),
SD = sd(Political_knowledge),
n = n(),
SE = SD / sqrt(n),
t_critical = qt(0.975, df = n - 1), # t-value for 95% CI
lower_ci = M - t_critical * SE,
upper_ci = M + t_critical * SE
)# A tibble: 1 × 7
M SD n SE t_critical lower_ci upper_ci
<dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl>
1 3.04 1.36 993 0.0432 1.96 2.96 3.13Berechnung der Konfidenzintervalle für Anteile
d |>
select(Facebook) |>
mutate(Facebook = as_factor(Facebook)) |>
report_sample(ci = 0.95)# Descriptive Statistics
Variable | Summary
-------------------------------------------------------
Facebook [Never], % | 49.5 [46.4, 52.7]
Facebook [Less than once a week], % | 8.1 [6.5, 9.9]
Facebook [1 to 2 times a week], % | 7.2 [5.7, 8.9]
Facebook [3 to 4 times a week], % | 6.8 [5.4, 8.6]
Facebook [(Almost) daily], % | 16.1 [14.0, 18.5]
Facebook [More than once a day], % | 12.3 [10.4, 14.5]Politisches Wissen nach Gender
d |>
select(Political_knowledge, Gender) |>
report_sample(by = "Gender")# Descriptive Statistics
Variable | male (n=519) | female (n=474) | Total (n=993)
-----------------------------------------------------------------------------
Mean Political_knowledge (SD) | 3.44 (1.32) | 2.61 (1.28) | 3.04 (1.36)T-Test zum Vergleich der Mittelwerte von Männern und Frauen Tabelle
t.test(Political_knowledge ~ Gender, data = d) |>
report_table(data = d)Welch Two Sample t-test
Parameter | Group | Mean_Group1 | Mean_Group2 | Difference
---------------------------------------------------------------------
Political_knowledge | Gender | 3.44 | 2.61 | 0.84
Parameter | 95% CI | t(987.31) | p | Cohen's d | Cohen's d CI
-----------------------------------------------------------------------------------
Political_knowledge | [0.67, 1.00] | 10.15 | < .001 | 0.64 | [0.52, 0.77]
Alternative hypothesis: two.sidedT-Test zum Vergleich der Mittelwerte von Männern und Frauen Text
t.test(Political_knowledge ~ Gender, data = d) |>
report(data = d)Effect sizes were labelled following Cohen’s (1988) recommendations.
The Welch Two Sample t-test testing the difference of Political_knowledge by Gender (mean in group male = 3.44, mean in group female = 2.61) suggests that the effect is positive, statistically significant, and medium (difference = 0.84, 95% CI [0.67, 1.00], t(987.31) = 10.15, p < .001; Cohen’s d = 0.64, 95% CI [0.52, 0.77])
Kreuztabelle Traditionelle Mediennutzung nach Gender
xtabelle <- d |>
data_tabulate(
select = "trad", by = "Gender",
remove_na = TRUE, proportions = "column"
)
xtabelletrad | male | female | Total
---------------------------+-------------+-------------+------
traditional news diet: no | 259 (49.9%) | 313 (66.0%) | 572
traditional news diet: yes | 260 (50.1%) | 161 (34.0%) | 421
---------------------------+-------------+-------------+------
Total | 519 | 474 | 993Chi-Quadrat-Test Traditionelle Mediennutzung nach Gender Tabelle
xtabelle |>
as.table(simplify = TRUE) |>
chisq.test() |>
report_table(data = d)Pearson's Chi-squared test with Yates' continuity correction
Chi2(1) | p | Cramer's V (adj.) | Cramers_v_adjusted CI
-------------------------------------------------------------
25.74 | < .001 | 0.16 | [0.11, 1.00]Chi-Quadrat-Test Traditionelle Mediennutzung nach Gender Text
xtabelle |>
as.table(simplify = TRUE) |>
chisq.test() |>
report(data = d)Effect sizes were labelled following Funder’s (2019) recommendations.
The Pearson’s Chi-squared test with Yates’ continuity correction of independence between suggests that the effect is statistically significant, and small (chi2 = 25.74, p < .001; Adjusted Cramer’s v = 0.16, 95% CI [0.11, 1.00])
3.4 Hausaufgabe
1) Vollziehen Sie die Analysen nach, deren Ausgaben wir in der Vorlesung besprochen haben.
- Schreiben Sie kurze Ergebnistexte zur Beantwortung der Fragen bzw. zum Test der Hypothesen:
- Wie viele der fünf Wissensfragen beantworten Menschen in Flandern durchschnittlich korrekt?
- Welcher Anteil der Flamen nutzt nie Facebook zur politischen Information?
- Wie groß ist der Wissensunterschied zwischen Männern und Frauen in Flandern?
- Die Verbreitung eines traditionellen Medienrepertoires unterscheidet sich zwischen Männern und Frauen.
- Männer wissen mehr über Politik als Frauen.
2) Prüfen Sie die Hypothese: Personen mit einem traditionellen Medienrepertoire unterscheiden sich in ihrem politischen Wissen von Personen, die ein anderes Medienrepertoire haben.
Lösung
- Zu 1) Siehe Code und Ausgaben aus der Vorlesung
- Zu 2) R Skript | HTML mit Output
3.5 Transkript Teil 1 (Vorlesungssitzung 3)
Das folgende Transkript wurde auf Basis der Aufzeichnung der Vorlesung erstellt. Die vollständige Aufzeichnungen inklusive der Bildschirminhalte sind in Blackboard🔒 verfügbar. Die Tonspur wurde mit VoiceAI transkribiert. Das Transkript wurde dann mit Sprachmodellen (v.a. Claude Sonnet 4.5) geglättet und formatiert. In diesem Prozess kann es an verschiedenen Stellen zu Fehlern kommen. Im Zweifel gilt das gesprochene Wort, und auch beim Vortrag mache ich Fehler.
Ich stelle das Transkript hier als experimentelles, ergänzendes Material zur Dokumentation der Vorlesung zur Verfügung. Noch bin ich mir unsicher, ob es eine sinnvolle Ergänzung ist und behalte mir vor, es weiter zu bearbeiten oder zu löschen.
Einführung in die Inferenzstatistik
Inferenzstatistik ist der Teil der Statistik, bei dem Aussagen über eine Grundgesamtheit getroffen werden. Es geht nicht mehr nur um die Beschreibung der Stichprobe, sondern um allgemeingültige Aussagen über die Population, aus der die Stichprobe stammt.
Inferenzstatistik besteht aus zwei Bereichen: Schätzen von Populationsparametern und Hypothesentesten. Beim Schätzen wird gefragt, wie ein in der Stichprobe berechneter Wert in der Grundgesamtheit aussieht. Beispielsweise: Wie viele Fragen beantworten Menschen in Flandern im Durchschnitt richtig? Welcher Anteil der Flamen nutzt nie Facebook zur politischen Information? Wie groß ist der Wissensunterschied zwischen Männern und Frauen in der Grundgesamtheit?
Beim Hypothesentesten werden theoretisch abgeleitete Hypothesen anhand von Daten geprüft. Die Theorie ermöglicht Vorhersagen über erwartete Befunde. Nach der Datenerhebung wird geprüft, ob die Daten die Theorie stützen oder sie verworfen werden muss. Beispiele für Hypothesen: Wissen Männer mehr über Politik als Frauen? Gibt es einen Zusammenhang zwischen Alter und politischem Wissen?
Die in der Regel verwendete Form ist die frequentistische Inferenzstatistik. Dies ist die Statistik, die üblicherweise im Bachelor gelehrt wird. Frequentistisch bedeutet, dass Wahrscheinlichkeiten und Fehler als Ergebnisse vieler Wiederholungen von Studien verstanden werden. Die Grundidee: Wenn die gleiche Studie viele Male wiederholt würde (mit jeweils neuen Zufallsstichproben), wie oft würden die gleichen Ergebnisse gefunden?
Es geht um langfristige Irrtumswahrscheinlichkeiten. Wenn korrekt frequentistisch gearbeitet wird, bedeutet dies, dass langfristig nur ein kleiner Anteil der Schlussfolgerungen falsch ist. Beispiel: Bei korrekter Anwendung sind nur 5% der Aussagen falsch, 95% der Aussagen sind korrekt. Allerdings ist nie bekannt, welcher konkrete Fall richtig oder falsch ist. Dies ist eine wichtige Eigenschaft für die Wissenschaft: Aussagen sind meistens korrekt, manchmal nicht, aber es ist nicht für jeden Einzelfall bekannt.
Frequentistische Inferenzstatistik ist in den Sozialwissenschaften am weitesten verbreitet. Erkennungsmerkmale sind Konfidenzintervalle, p-Werte und statistische Signifikanz.
Es gibt jedoch auch andere Formen der Statistik. Eine Alternative ist die Bayesianische Inferenzstatistik, die zunehmend populärer wird. Früher war sie praktisch schwer durchführbar, aber verbesserte Computer machen sie heute praktikabler.
Der Standardfehler
Ein zentrales Konzept in der frequentistischen Inferenzstatistik ist der Standardfehler. Dieses Konzept ist schwierig zu erklären und wird häufig mit anderen Konzepten verwechselt, da die Namensgebung in der Statistik nicht immer eindeutig ist.
Zunächst zur Standardabweichung (SD, von Standard Deviation): Die Standardabweichung beschreibt, wie typisch der Mittelwert einer Variable für die Stichprobe ist. Sie gibt die durchschnittliche Abweichung vom Mittelwert an.
Der Standardfehler ist hingegen die Streuung der Schätzungen einer Kennzahl bei wiederholter Durchführung der gleichen Studie. Wenn immer wieder 993 zufällig ausgewählte Personen aus Flandern befragt würden und jedes Mal der Mittelwert des politischen Wissens berechnet würde, dann gibt der Standardfehler an, wie stark diese Mittelwerte streuen würden.
Der Standardfehler sagt also nichts über die Stichprobe selbst aus, sondern ist ein Maß dafür, wie typisch das Stichprobenergebnis für die Grundgesamtheit ist.
In klassischen Statistikvorlesungen wird ausführlich abgeleitet, wie Standardfehler geschätzt werden. Dies erfolgt hier nicht im Detail. Wichtig ist: Der Standardfehler gibt an, wie typisch eine berechnete Kennzahl wahrscheinlich für die Grundgesamtheit ist.
In der Inferenzstatistik wird der Standardfehler auf Basis der Stichprobe geschätzt. Die Stichprobe ist das einzige vorliegende Material. Der Mittelwert wird berechnet, dann wird der Standardfehler auf Basis der Stichprobe geschätzt. Anschließend werden Annahmen aus der frequentistischen Inferenzstatistik verwendet, um aus dem Standardfehler abzuleiten, wie unsicher die Inferenzschlüsse sind.
Der Standardfehler ist ein Werkzeug, um die in der Stichprobe vorliegende Evidenz einzuschätzen und zu beurteilen, wie sicher oder unsicher Schlussfolgerungen auf die Grundgesamtheit sind.
Wichtig: Der Betrag des Standardfehlers wird in der Regel nicht interpretiert. Es interessiert nicht, ob der Standardfehler 0,03 oder ein anderer Wert ist. Der Standardfehler wird immer mit anderen Stichprobenwerten verrechnet, um Informationen darüber zu erhalten, wie gut ein Wert auf die Grundgesamtheit übertragbar ist.
Der Standardfehler hilft dabei auszusagen, wie viel Information in den Daten enthalten ist und wie unsicher Schlussfolgerungen von den Daten auf die Grundgesamtheit sein müssen. Für jede Statistik gibt es eine Form von Standardfehler, der angibt, wie gut das Stichprobenergebnis auf die Grundgesamtheit übertragen werden kann.
Aus dem Standardfehler können beispielsweise Fehlerspannen berechnet werden, wie sie häufig in Umfragen angegeben werden.
3.6 Transkript Teil 2 (Vorlesungssitzung 4)
Das folgende Transkript wurde auf Basis der Aufzeichnung der Vorlesung erstellt. Die vollständige Aufzeichnungen inklusive der Bildschirminhalte sind in Blackboard🔒 verfügbar. Die Tonspur wurde mit VoiceAI transkribiert. Das Transkript wurde dann mit Sprachmodellen (v.a. Claude Sonnet 4.5) geglättet und formatiert. In diesem Prozess kann es an verschiedenen Stellen zu Fehlern kommen. Im Zweifel gilt das gesprochene Wort, und auch beim Vortrag mache ich Fehler.
Ich stelle das Transkript hier als experimentelles, ergänzendes Material zur Dokumentation der Vorlesung zur Verfügung. Noch bin ich mir unsicher, ob es eine sinnvolle Ergänzung ist und behalte mir vor, es weiter zu bearbeiten oder zu löschen.
