Call:
lm(formula = Political_knowledge ~ Age, data = d)
Coefficients:
(Intercept) Age
1.4761 0.0296 (Wiederholung:) Bivariate lineare Regression
Methoden der empirischen Kommunikations- und Medienforschung
Freie Universität Berlin
Heute: (Wiederholungssitzung)
- Viele haben bereits Erfahrung mit der bivariaten Korrelation ([Pearsons] r), einige auch mit der linearen Regression. In dieser Sitzung werden wir unter anderem lernen, dass der Korrelationskoeffizient r nur eine spezielle Art ist, das Ergebnis einer bivariaten linearen Regression darzustellen.
Agenda
- Grundlagen der Regression
- Regression und Mittelwertvergleich
- Annahmen und ihre Überprüfung
- Transformation von Variablen
- Zusammenfassung
- Übungsaufgaben
Daten der heutigen Sitzung

Warum so viel Regression?
Warum so viel Regression?
Grundlagen der Regression
Grundlagen der Regression
Frage: Welche (lineare) Beziehung besteht zwischen zwei metrischen Variablen?
Funktion: Beschreibung der bivariaten Verteilung zweier metrischer Variablen
Konvention: Mit Regression ist meist eine lineare Regression mit OLS-Schätzung (ordinary least squares, Methode der kleinsten Quadrate) gemeint
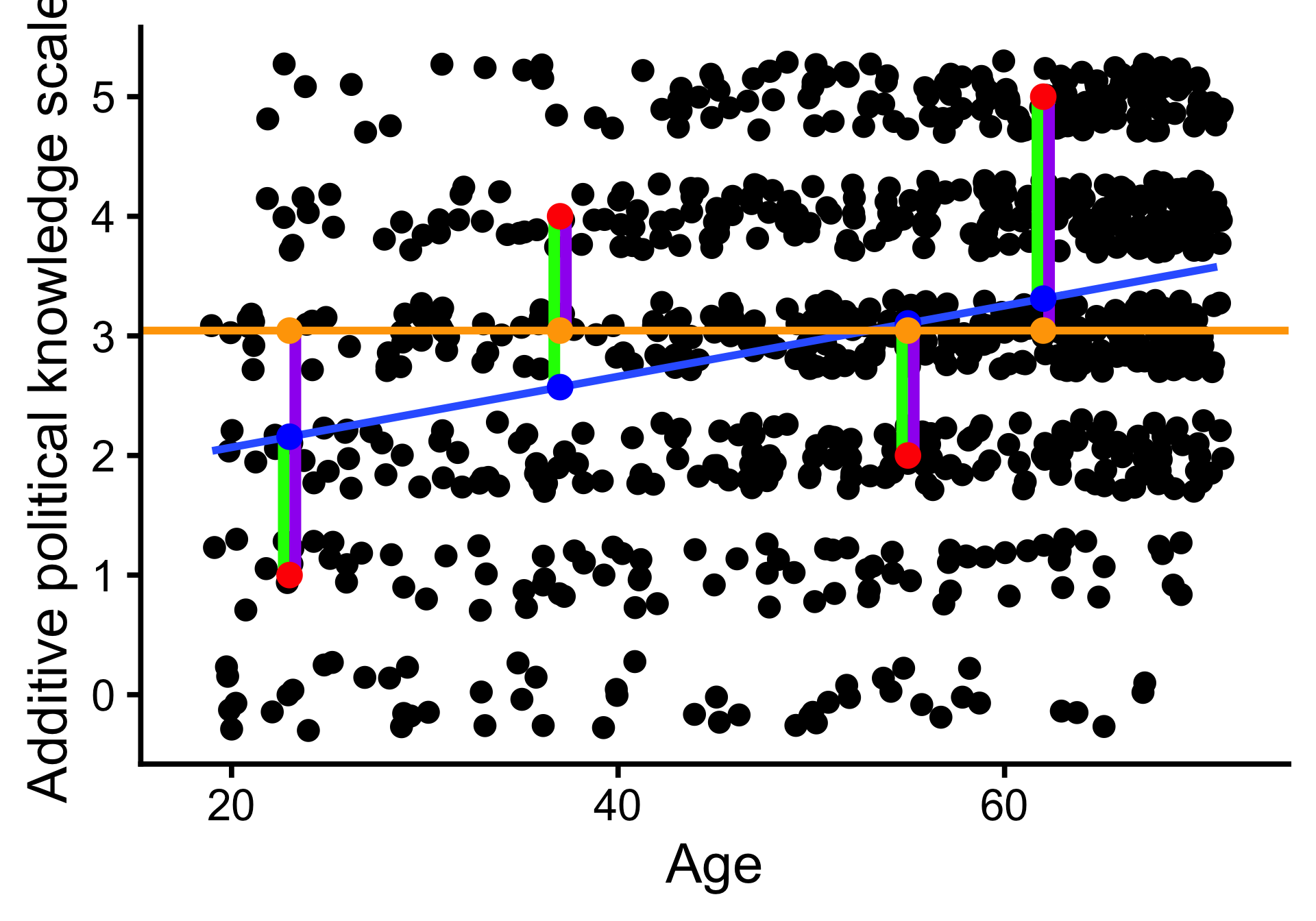
Scatterplot und Regressionsgerade

Jittered scatterplot und Regressionsgerade
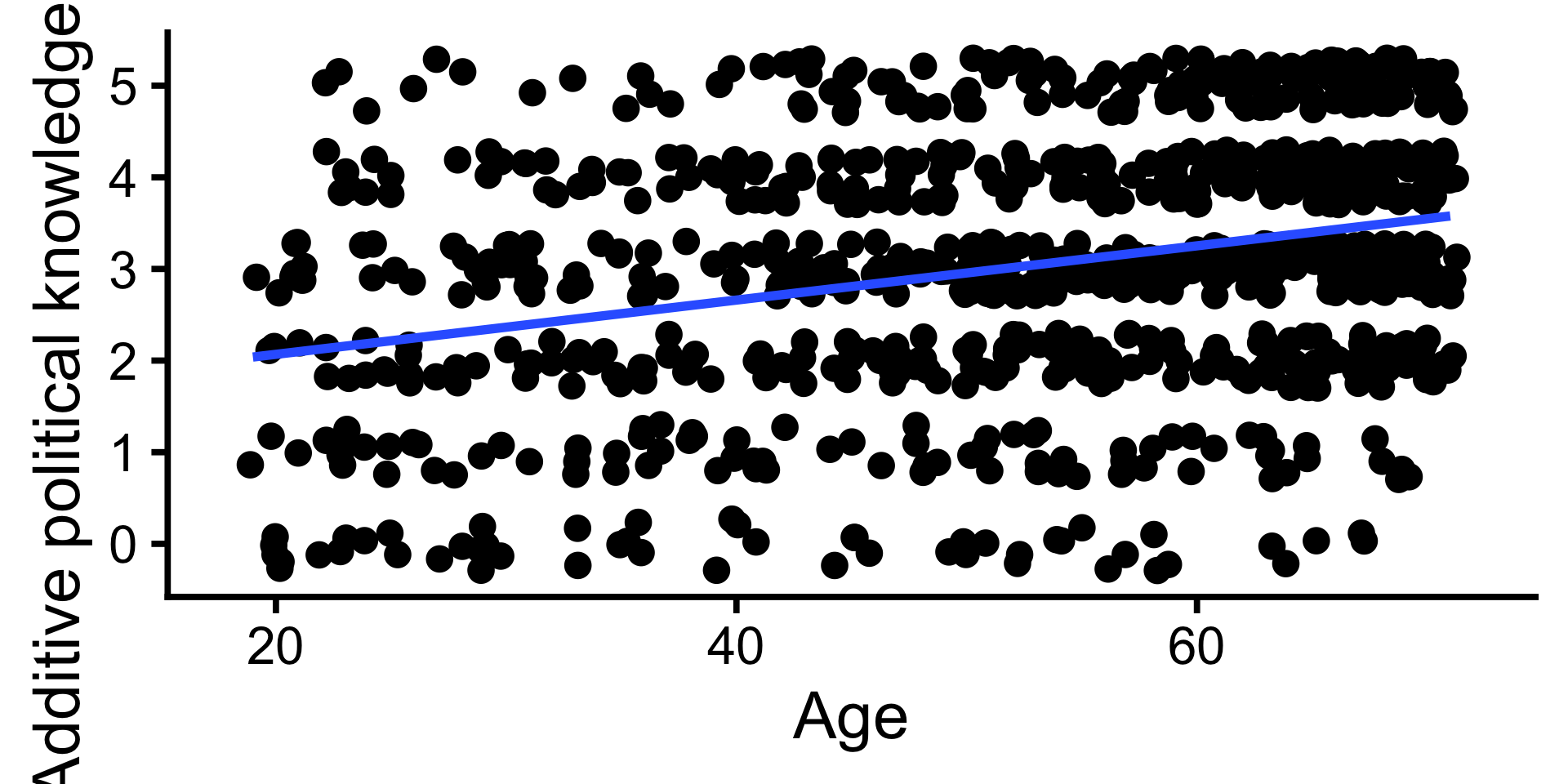
Koeffizienten
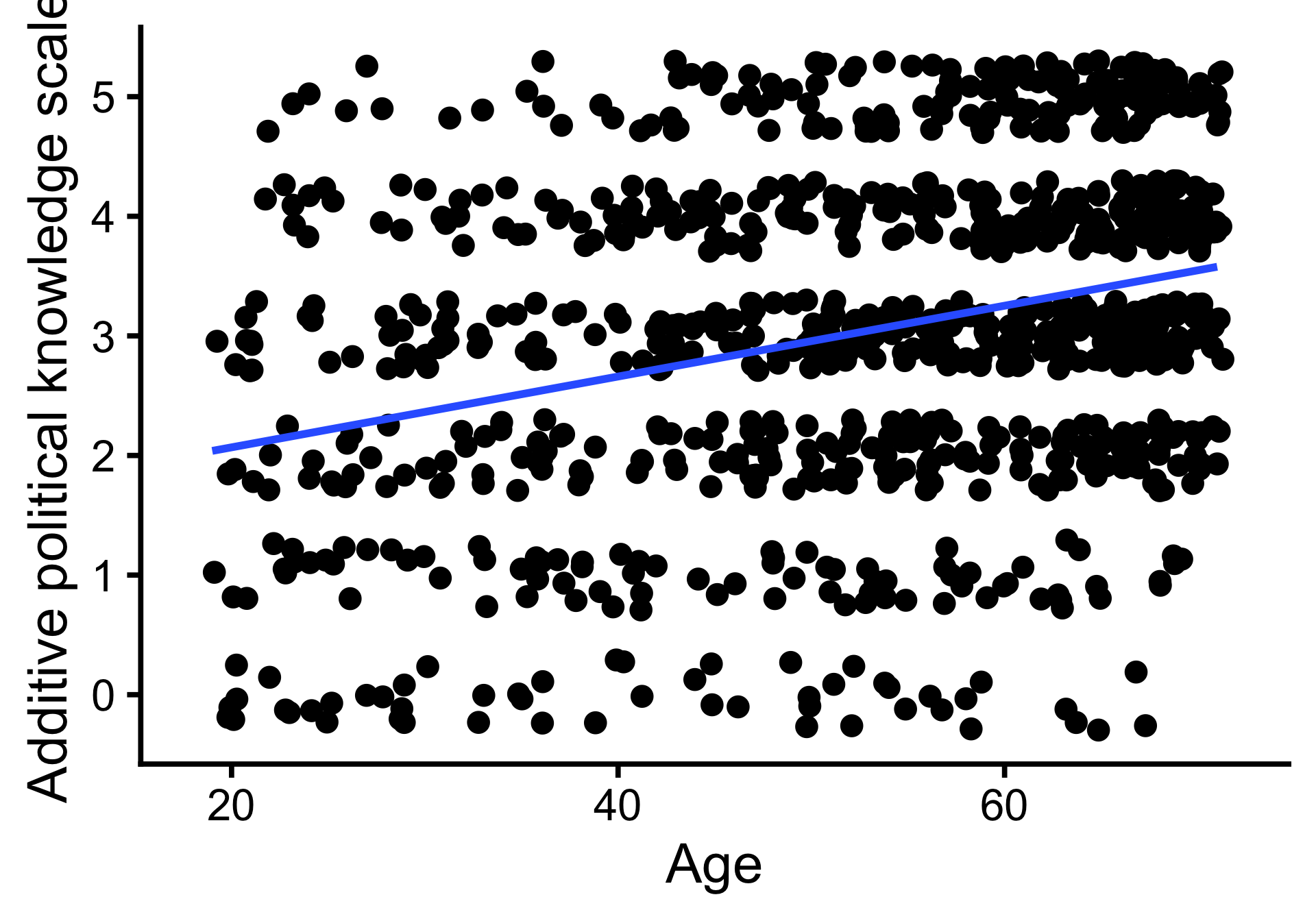
Koeffizienten
- In der bivariaten Regression wird eine Gerade durch die Punkte des Streudiagramms gelegt
- Die Gerade wird durch die durch eine lineare Gleichung mit zwei Koeffizienten definiert:
- allgemein: \(y = b_0 + b_1 * x\)
- hier: \(\text{Political_knowledge} = 1.48 + 0.03 * \text{Age}\)
- Mit \(b_0\) Schnittpunkt mit Y-Achse (Konstante, Intercept) und \(b1\) Steigung der Gerade (Slope)
- \(b_0\): Wenn Age den Wert 0 hat, dann hat Political_knowledge den Wert 1.48.
- \(b_1\): Wenn Age um 1 Jahr steigt, dann steigt Political_knowledge um 0.03.
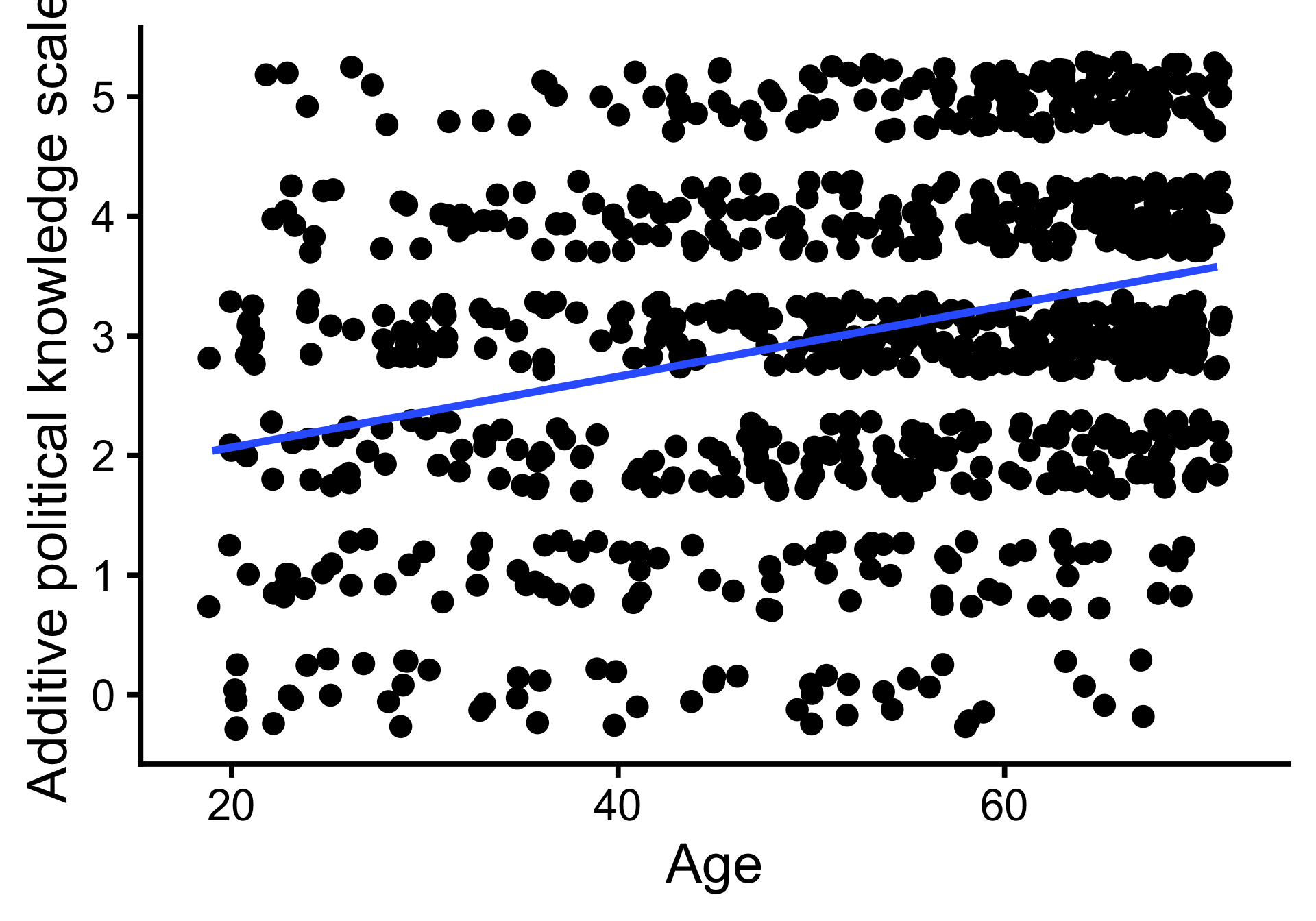
Schätzung
Beispiel für vier Befragte:
| Age | y | yhat | e | e2 |
|---|---|---|---|---|
| 23 | 1 | 2.16 | -1.16 | 1.34 |
| 37 | 4 | 2.57 | 1.43 | 2.04 |
| 55 | 2 | 3.10 | -1.10 | 1.22 |
| 62 | 5 | 3.31 | 1.69 | 2.85 |
- \(y\): Beobachteter Wert
- \(\hat y\): Vorhergesagter Wert
- \(e\): Residuum, Vorhersagefehler
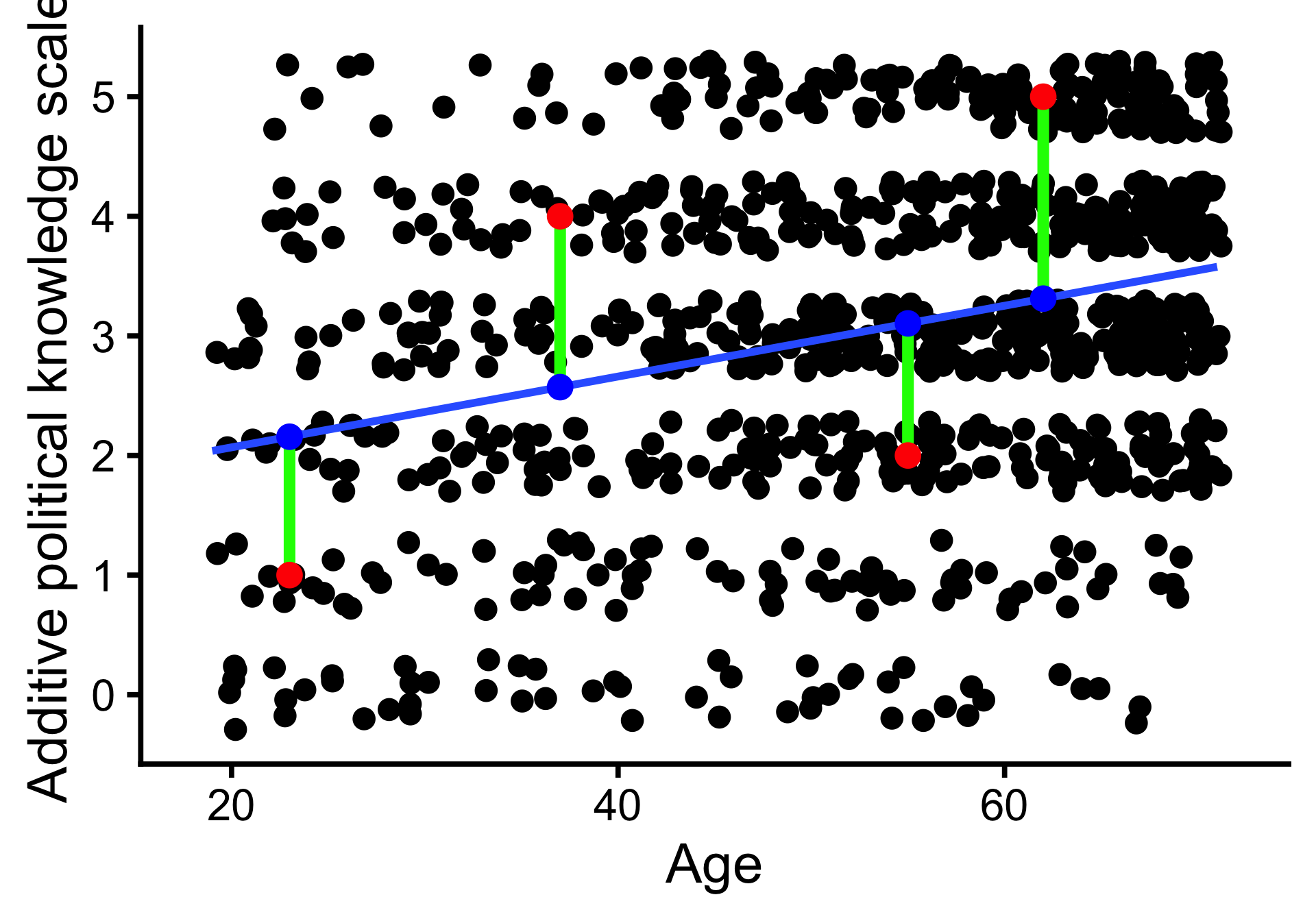
Die Regressionsgerade minimiert die Fehlerquadratsumme.
Mit OLS-Schätzung: \(b_1 = \frac{\sum (x_i - \bar{x}) \times (y_i - \bar{y})}{\sum (x_i - \bar{x})^2}\) und \(b_0 = \bar{y} - b_1 \times \bar{x}\) oder in Matrix-Notation \(\beta = (X^TX)^{-1}X^TY\)
\(R^2\)
Beispiel für vier Befragte:
| Age | y | yhat | e | e2 | e_M | e_M2 |
|---|---|---|---|---|---|---|
| 23 | 1 | 2.16 | -1.16 | 1.34 | -2.04 | 4.18 |
| 37 | 4 | 2.57 | 1.43 | 2.04 | 0.96 | 0.91 |
| 55 | 2 | 3.10 | -1.10 | 1.22 | -1.04 | 1.09 |
| 62 | 5 | 3.31 | 1.69 | 2.85 | 1.96 | 3.82 |
- \(y\): Beobachteter Wert
- \(\hat y\): Vorhergesagter Wert
- \(e\): Residuum, Vorhersagefehler
- \(\bar y\): Mittelwert
- \(e_m\): Abweichung vom Mittelwert
\(R^2 = \frac{\sum(y_i - \bar{y})^2 - \sum(y_i - \hat y)^2}{\sum(y_i - \bar{y})^2}\)
- \(R^2 = .09\): Anteil der Varianz, die das Regressionsmodell erklärt; 0 (Modell erklärt keine Varianz) bis 1 (perfekter linearer Zusammenhang). Vergleich mit Mittelwert als einfachstem Modell von \(y\).
\(R^2\)
Standardisierung und (Pearsons) \(r\)
- Standardisierter Regressionskoeffizient (unter SPSS-Nutzer:innen häufig \(\beta\)): \(\beta_1 = b_1 \times \frac{SD_x}{SD_y}\)
- Schätzung nach z-Standardisierung der Daten: \((x_i - M_x) / SD_x\) mit \(M_x\) Mittelwert von \(x\) und \(SD_x\) Standardabweichung von \(x\)
- \(\text{Z_Political_knowledge} = 0.30 * \text{Z_Age}\); \(SD_{\text{Age}} = 14\), \(SD_{\text{Political_knowledge}} = 1.4\)
- Wenn das Alter um 1 SD steigt, dann steigt Political_knowledge um 0.30 SD.
- Korrelationskoeffizient Pearsons \(r\) = standardisierter Regressionskoeffizient in bivariater linearer Regression; hier: \(r = 0.30 = \beta_1\)
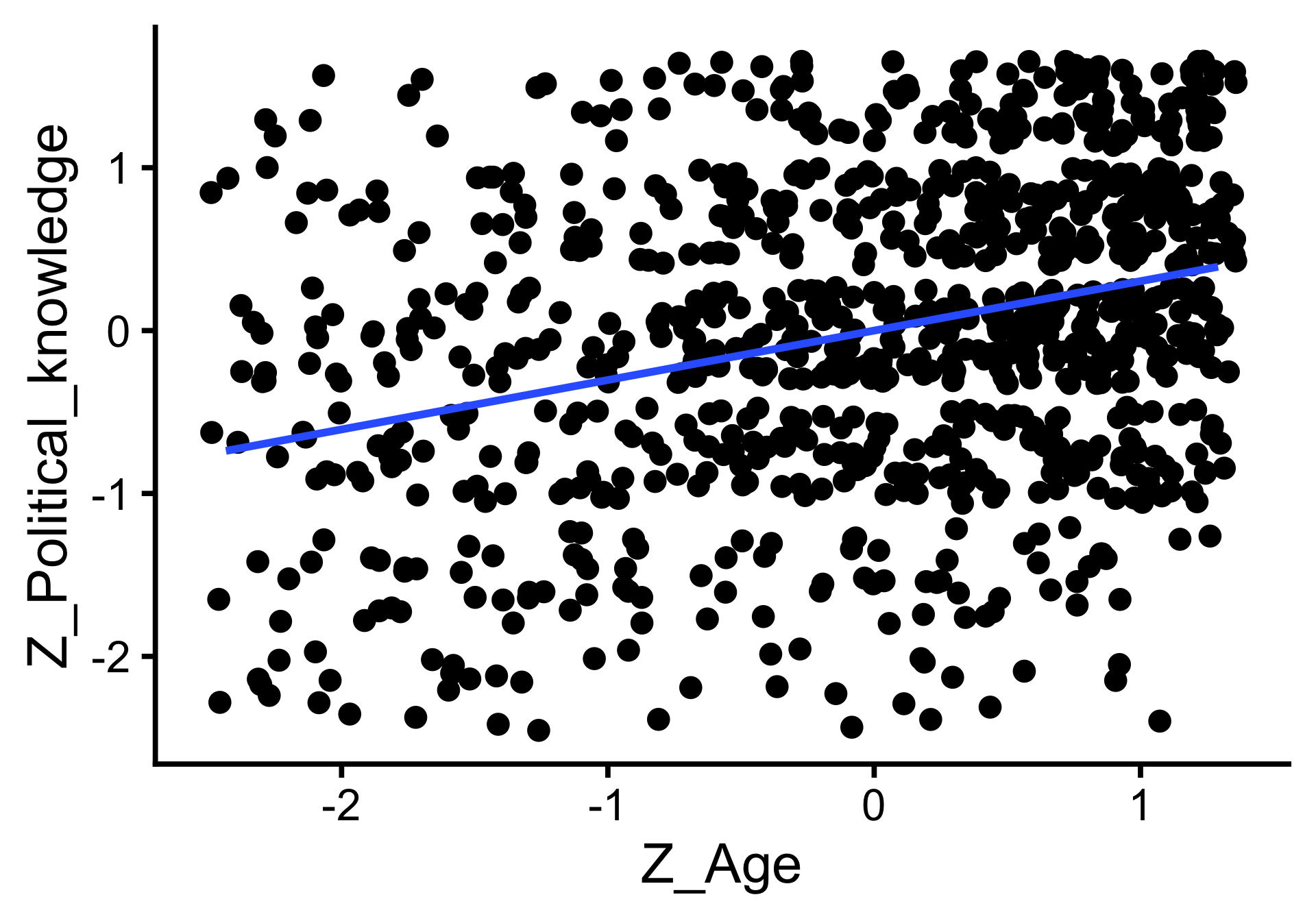
Standardisierung und (Pearsons) \(r\)
Vergleich in R
Inferenzstatistik zur Regression
| Parameter | Coefficient | 95% CI | t(991) | p | Std. Coef. | Std. Coef. 95% CI | Fit |
|---|---|---|---|---|---|---|---|
| (Intercept) | 1.48 | (1.16, 1.79) | 9.12 | < .001 | 0.00 | (-0.06, 0.06) | |
| Age | 0.03 | (0.02, 0.04) | 10.02 | < .001 | 0.30 | (0.24, 0.36) | |
| R2 | 0.09 |
Inferenzstatistik zur Korrelation
r = 0.30, 95% CI [0.25, 0.36], t(991) = 10.02, p < .001
Vorhersagen: Tabelle
| Age | Estimate | Std. Error | z | Pr(>|z|) | S | 2.5 % | 97.5 % |
|---|---|---|---|---|---|---|---|
| Type: response | |||||||
| 39.0 | 2.63 | 0.0583 | 45.1 | <0.001 | Inf | 2.52 | 2.75 |
| 53.0 | 3.04 | 0.0412 | 73.9 | <0.001 | Inf | 2.96 | 3.13 |
| 66.9 | 3.46 | 0.0583 | 59.3 | <0.001 | Inf | 3.34 | 3.57 |
- Mit der Regressionsgleichung lassen sich Vorhersagen der abhängigen Variable für beliebige Werte der Prädiktoren machen.
- Hier: Für Personen mit unterdurchschnittlichem (M - SD), durchschnittlichen (M) und überdurchschnittlichen (M + SD) Alter
Vorhersagen: Plot
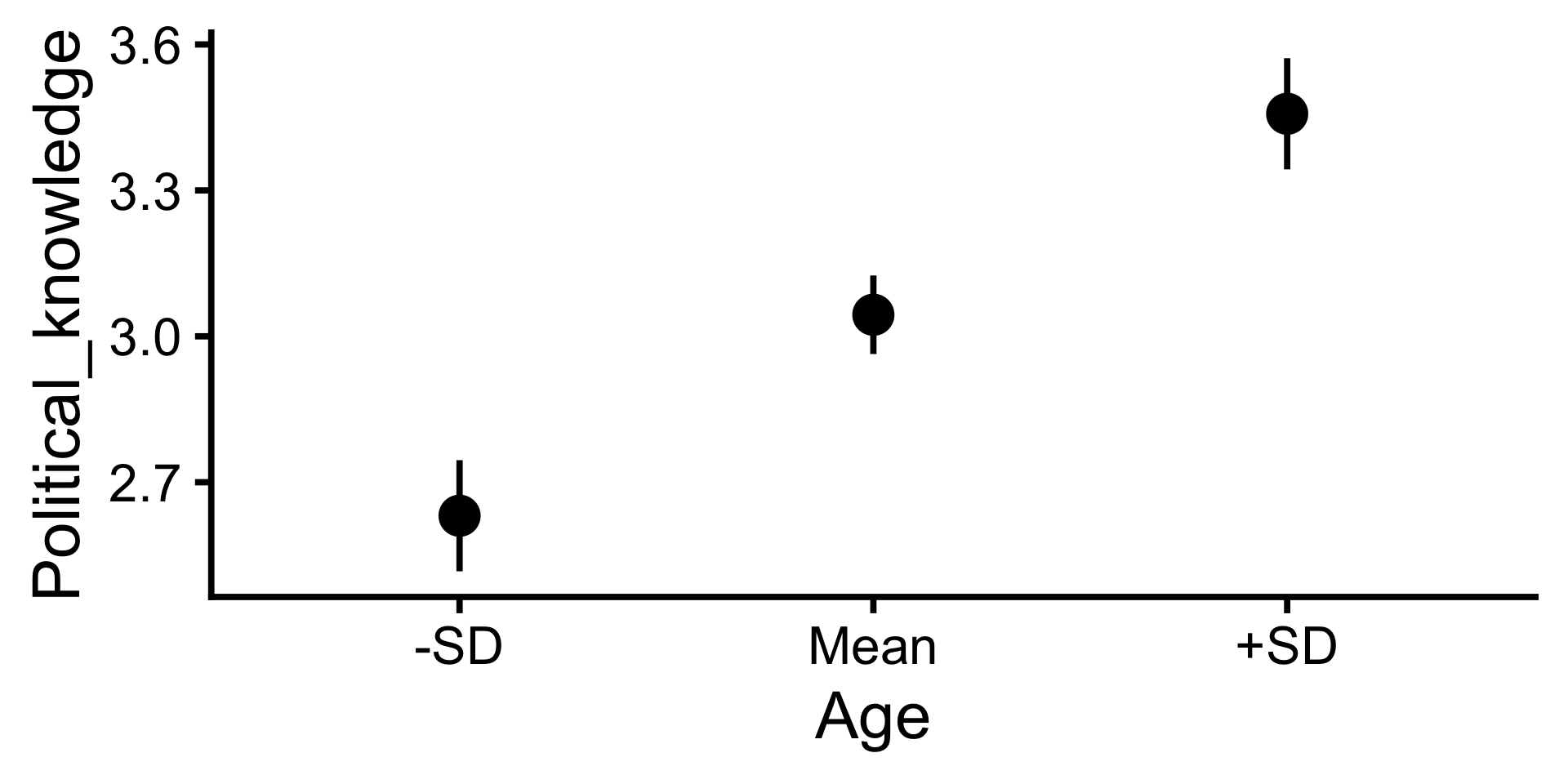
- Mit der Regressionsgleichung lassen sich Vorhersagen der abhängigen Variable für beliebige Werte der Prädiktoren machen.
- Hier: Für Personen mit unterdurchschnittlichem (M - SD), durchschnittlichen (M) und überdurchschnittlichen (M + SD) Alter
Interpretation
| Nicht standardisiert | Standardisiert (Korrelation) | |
|---|---|---|
| Vergleich (immer möglich) |
Wir vergleichen zwei Personen, die sich im Alter um ein Jahr unterscheiden. Die ältere Person beantwortet 0.03 Fragen mehr korrekt als die jüngere Person. | Wir vergleichen zwei Personen, die sich im Alter um eine SD unterscheiden. Die ältere Person liegt in der Verteilung der korrekt beantworteten Fragen Fragen um 0.3 SD über der jüngeren Person. |
| Veränderung, Intervention (kausal; zusätzliche Annahmen) | Wenn eine Person um ein Jahr älter wird, dann beantwortet sie 0.03 Fragen mehr korrekt. | Wenn eine Person sich in der Altersverteilung um eine SD nach oben bewegt, dann bewegt sie sich in der Verteilung der korrekt beantworteten Fragen um 0.3 SD nach oben. |
Fragen?
Regression und Mittelwertvergleich
Regression und Mittelwertvergleich
Wir können Mittelwertvergleiche innerhalb der linearen Regression durchführen.
In bivariater Analyse äquivalent zum \(T\)-Test. Interessanter in multipler Regression (Mittelwertvergleiche unter Berücksichtigung weiterer Variablen)
Binäre Prädiktoren (allgemein)
- Gruppierungsvariable \(X\) wird in eine Dummy-Variable recodiert (0 = Merkmal nicht vorhanden; Referenzgruppe, 1 = Merkmal vorhanden)
- Regressionsgerade: \(Y = b_0 + b_1 \times X + \varepsilon\)
- Wenn \(X = 0\): \(Y = b_0 + \varepsilon\)
- \(b_0\) ist Mittelwert der Referenzgruppe
- \(b_1\) ist Differenz zwischen Referenzgruppe und Gruppe mit Merkmal
Binäre Prädiktoren (Beispiel)
- \(\text{Gender}\) wird in eine Dummy-Variable \(\text{female}\) recodiert (0 = not female [hier: male], 1 = female)
- Regressionsgerade: \(Y = b_0 + b_1 \times \text{female} + \varepsilon\)
- Wenn \(\text{female} = 0\): \(Y = b_0 + \varepsilon\)
- \(b_0\) ist Mittelwert der Männer
- \(b_1\) ist Differenz zwischen Männern und Frauen
Regression
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 3.44 | (3.33, 3.55) | 60.48 | < .001 | |
| Gender (female) | -0.84 | (-1.00, -0.67) | -10.14 | < .001 | |
| R2 | 0.09 |
\(T\)-Test
| Parameter | Group | Mean_Group1 | Mean_Group2 | Difference | 95% CI | t(987.31) | p | Cohen’s d | Cohen’s d CI |
|---|---|---|---|---|---|---|---|---|---|
| Political_knowledge | Gender | 3.44 | 2.61 | 0.84 | (0.67, 1.00) | 10.15 | < .001 | 0.64 | (0.52, 0.77) |
Fragen?
Annahmen und ihre Überprüfung
Annahmen und ihre Überprüfung
Statistische Annahmen
- Linearität und Additivität der Zusammenhänge
- Normalverteilung und Homoskedastizität der Residuen
- Unabhängigkeit der Residuen
- keine einflussreichen Ausreißer
- (keine Multikollinearität) [→ Multiple Regression]
Kausalannahmen
- korrekt spezifiziertes Modell; keine fehlenden oder überflüssigen Variablen
- Besprechen wir in eigener Einheit
Annahmen und ihre Überprüfung
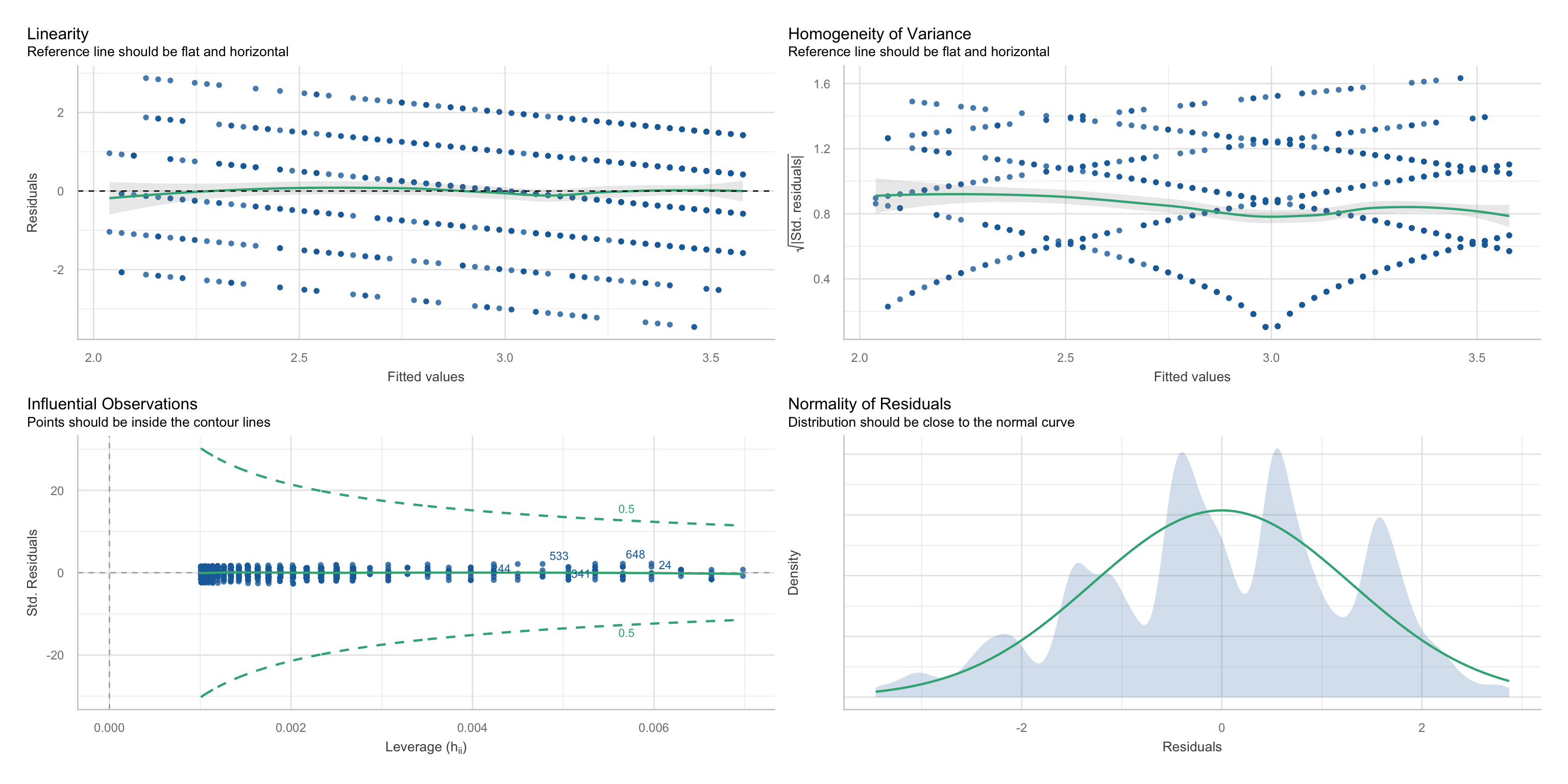
Linearität & Additivität
- Annahme: der Zusammenhang zwischen \(X\) und \(Y\) ist linear und unabhängig von \(Z\)
- Diagnose: Inspektion des Scatterplots bzw. des Fitted/Residual-Plots
- Verletzung: nichtlineare Zusammenhänge (quadratisch, exponentiell, etc.)
- Konsequenz der Verletzung: verzerrte Regressionskoeffizienten
- Lösung: Transformation von \(X\) oder \(Y\), nichtlineares Regressionsmodell, Moderationsanalyse mit \(Z\)
Linearität
$NCV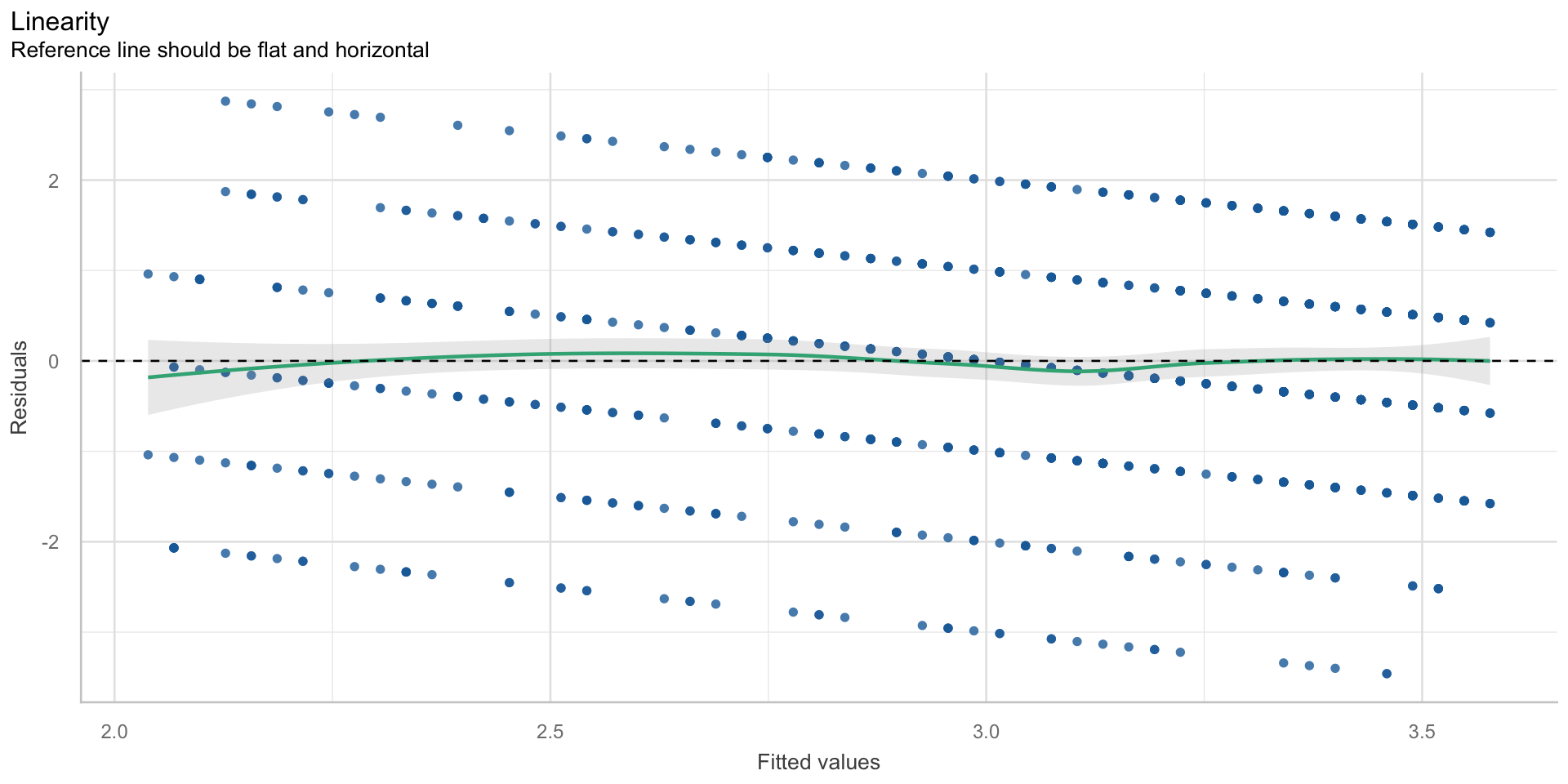
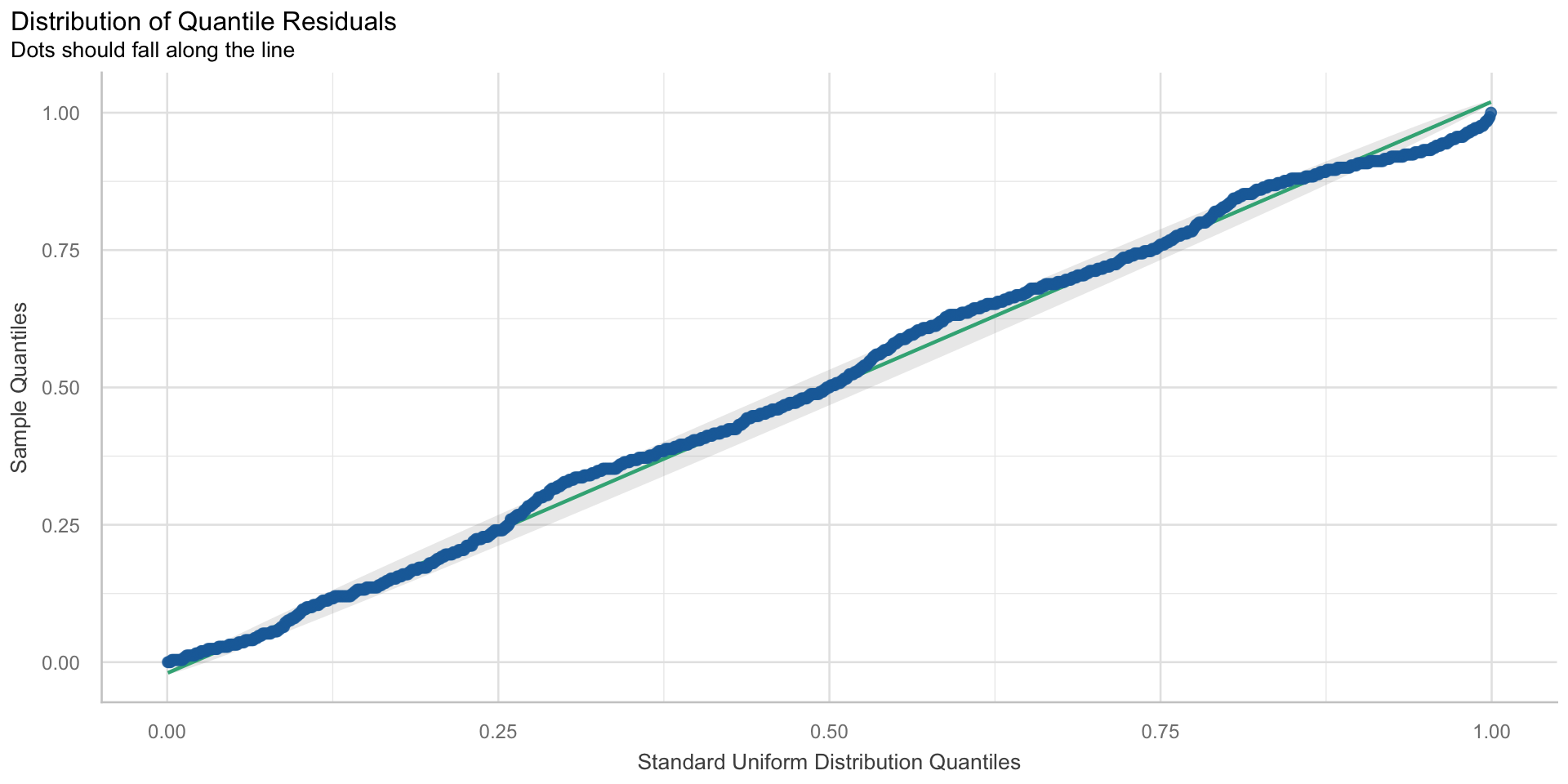
Normalverteilung der Residuen
- Annahme: Residuen sind normalverteilt
- Diagnose: Plot der Verteilung der Residuen
- Verletzung: Residuen sind nicht normalverteilt
- Konsequenz der Verletzung: falsche Standardfehler, ineffiziente Schätzung
- Lösung: alternative Standardfehler, Datentransformationen, alternatives Modell
Homoskedastizizät der Residuen
- Annahme: Residualvarianz ist für alle Werte von \(X\) gleich
- Diagnose: Fitted/Residual-Plots
- Verletzung: Residuen streuen in Abhängigkeit von \(X\)
- Konsequenz der Verletzung: falsche Standardfehler, ineffiziente Schätzung
- Lösung: alternative Standardfehler, Datentransformationen, alternatives Modell
Normalverteilung und Homoskedastizität der Residuen
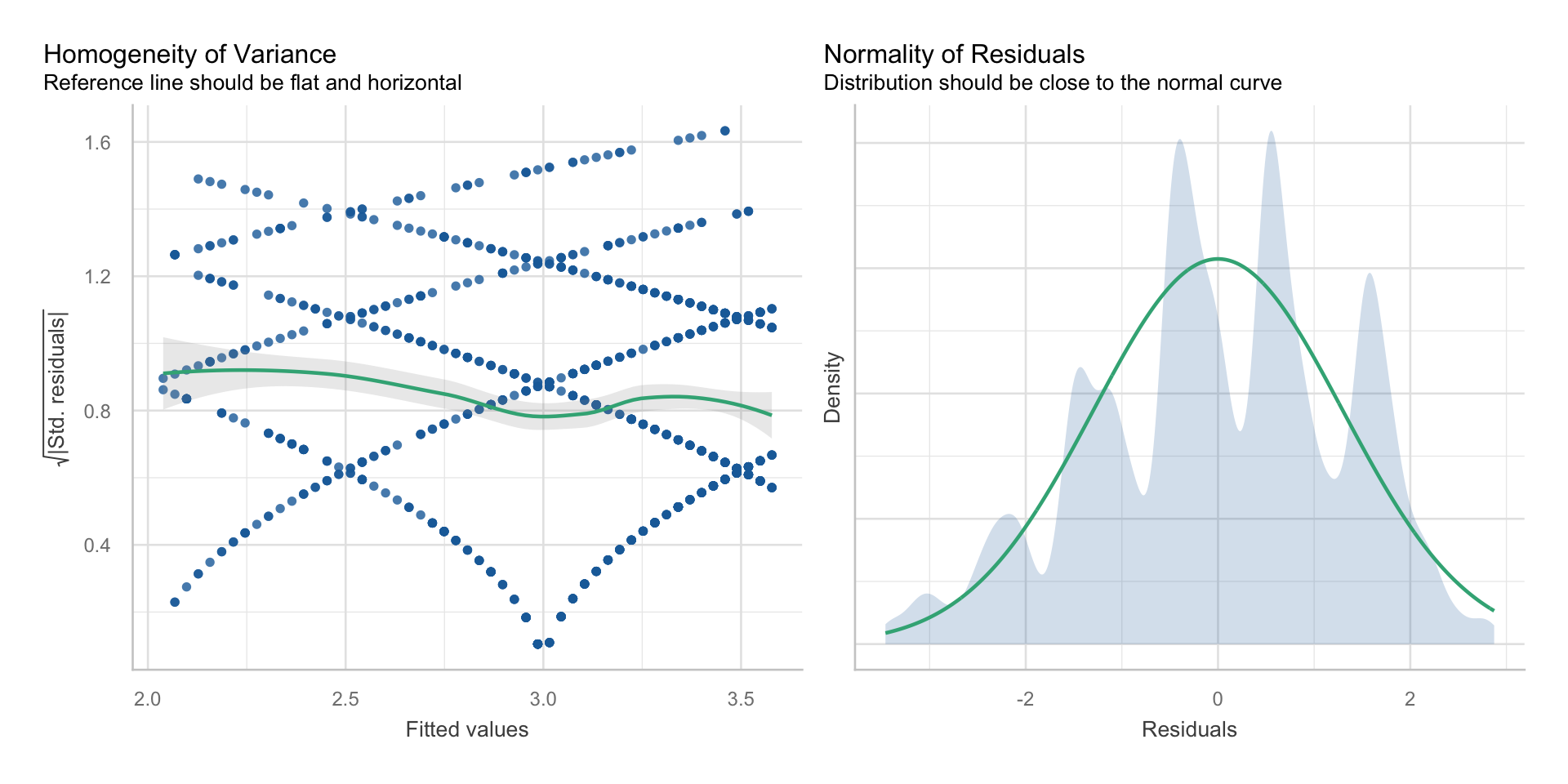
Unabhängigkeit der Residuen
- Annahme: Residuen korrelieren weder miteinander noch mit den Prädiktoren
- Diagnose: Nachdenken über datengenerierenden Prozess, Tests auf Zusammenhänge in Residuen
- Verletzung: Residuen (und oft Variablen) sind geclustert (zeitlich, Stichprobe)
- Konsequenz der Verletzung: falsche Standardfehler, ineffiziente Schätzung
- Lösung: Mehrebenen-Modell, Modell mit Autokorrelationen, alternative Standardfehler
Unabhängigkeit der Residuen
keine einflussreichen Ausreißer
- Annahme: alle Fälle tragen gleich zur Schätzung bei
- Diagnose: Scatterplot, Leverage-Plot
- Verletzung: einzelne Fälle beeinflussen die Höhe der Regressionsgeraden
- Konsequenz der Verletzung: verzerrte Regressionskoeffizienten
- Lösung: Ausschluss von Ausreißern (mit klar definierten Regeln!)
keine einflussreichen Ausreißer
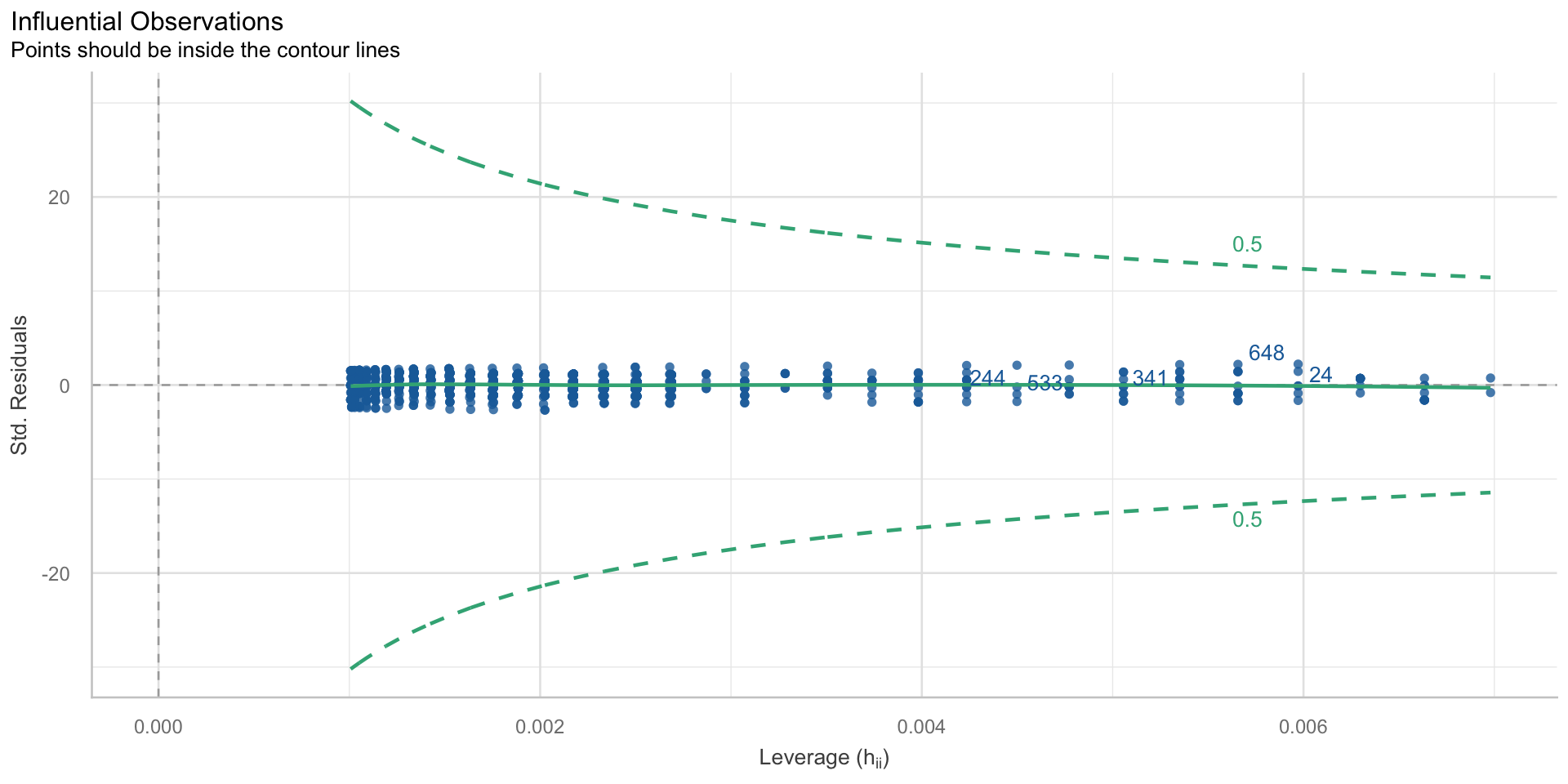
Verletzung der statistischen Modellannahmen - und nun?
- Keine Panik! Einige Modellannahmen sind praktisch immer verletzt (z.B. Normalverteilung der Residuen)
- Viele Annahmen beziehen sich auf die Residuen, nicht auf \(X\) oder \(Y\)
- Wichtig ist, einschätzen zu können, welche Konsequenzen eine Verletzung der Modellannahme haben kann
- verzerrte Schätzer (zu hoch, zu niedrig)
- falsche Standardfehler (\(\alpha\)- und \(\beta\)-Fehler)
- Vorsichtig formulieren, Robustheit der Ergebnisse prüfen
- Bei stärkeren Verletzungen Korrekturen möglich (robuste Schätzer, robuste Standardfehler; nicht in dieser Vorlesung)
- Problematischer sind Verletzungen der kausalen Annahmen (→ eigene Sitzung)
Fragen?
Transformation von Variablen im Regressionsmodell
Transformation von Variablen im Regressionsmodell
- Addieren & Subtrahieren einer Konstante: Ändert die Bedeutung der Konstante (Intercept) (Wert, wenn alle Prädiktoren gleich 0 sind)
- Multiplizieren & Dividieren mit einer Konstante: Ändert die Skala der Regressionskoeffizienten
- Nicht-lineare Transformationen eines Prädiktors (z.B. Quadrieren, Logarithmus): Ändert die funktionale Form der Beziehung
- (Multiplikation mehrerer Prädiktoren: Moderation & Interaktion) [→ eigene Einheit]
Addieren & Subtrahieren einer Konstante
- Zentrieren von quasi-metrischen Prädiktoren um ihren Mittelwert
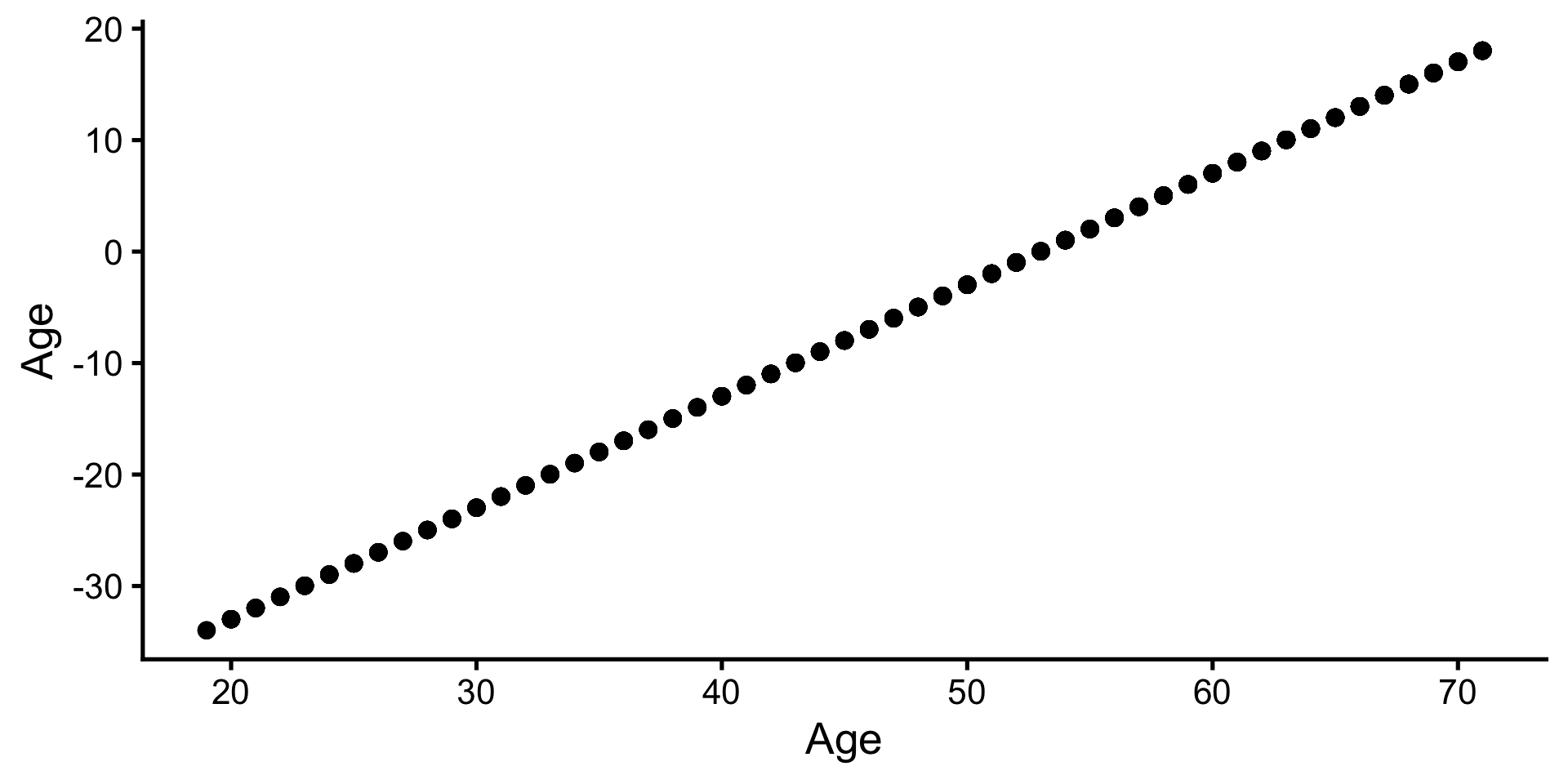
Addieren & Subtrahieren einer Konstante
Original
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 1.48 | (1.16, 1.79) | 9.12 | < .001 | |
| Age | 0.03 | (0.02, 0.04) | 10.02 | < .001 | |
| R2 | 0.09 |
Zentriert
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 3.04 | (2.96, 3.13) | 73.88 | < .001 | |
| Age c | 0.03 | (0.02, 0.04) | 10.02 | < .001 | |
| R2 | 0.09 |
Multiplizieren & Dividieren mit einer Konst.
- Skala verändern:
- Teilen des Alters durch 10 → Vergleich zu bzw. Veränderung um 10 Jahren

Multiplizieren & Dividieren mit einer Konst.
Original
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 1.48 | (1.16, 1.79) | 9.12 | < .001 | |
| Age | 0.03 | (0.02, 0.04) | 10.02 | < .001 | |
| R2 | 0.09 |
Transformiert
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 1.48 | (1.16, 1.79) | 9.12 | < .001 | |
| Age 10 | 0.30 | (0.24, 0.35) | 10.02 | < .001 | |
| R2 | 0.09 |
Multiplizieren & Dividieren mit einer Konst.
- Z-Standardisieren: Zentrieren aller quasi-metrischer Variablen um Mittelwert und Teilen durch eine Standardabweichung → Standardisierte Koeffizienten
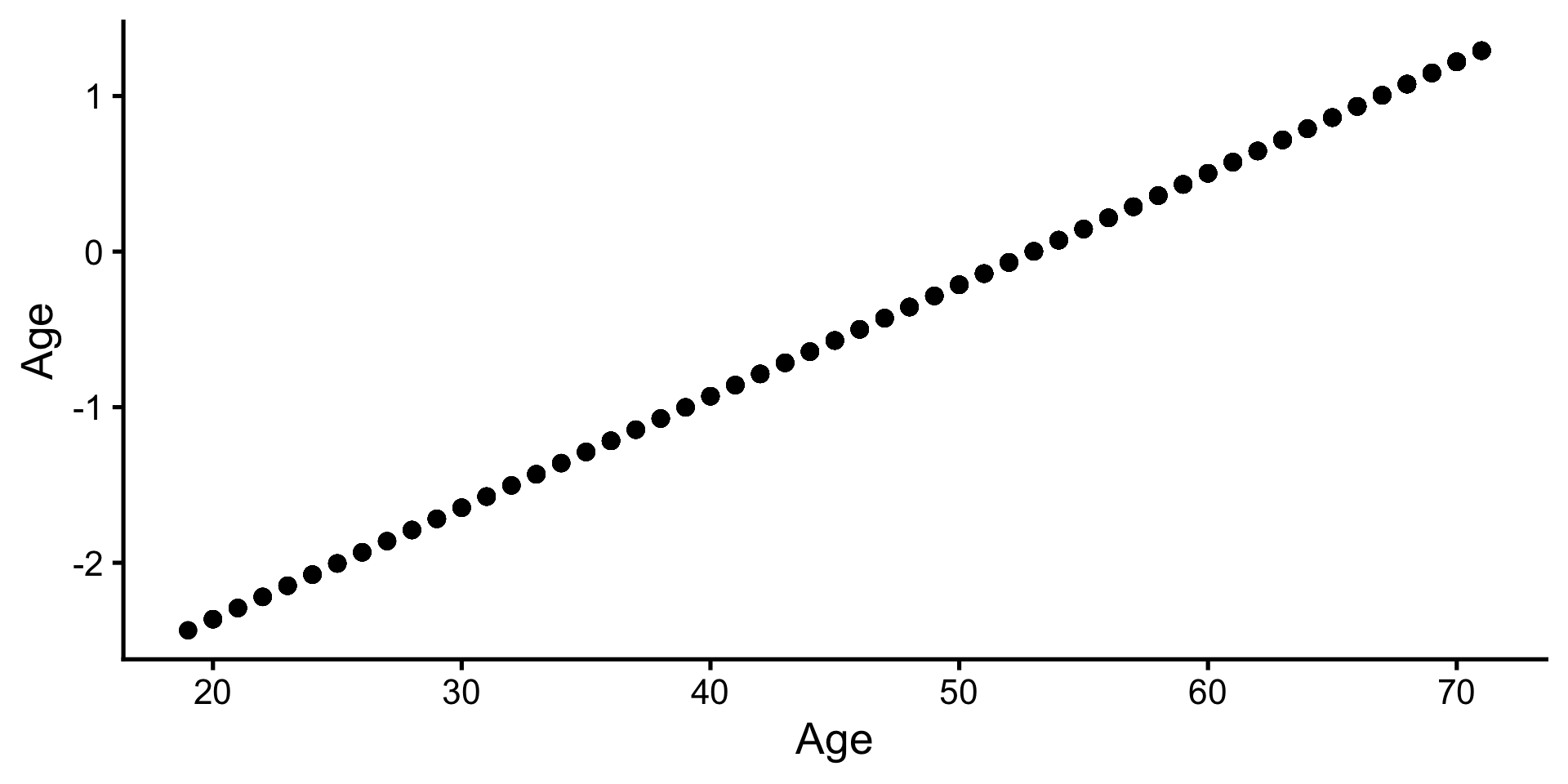
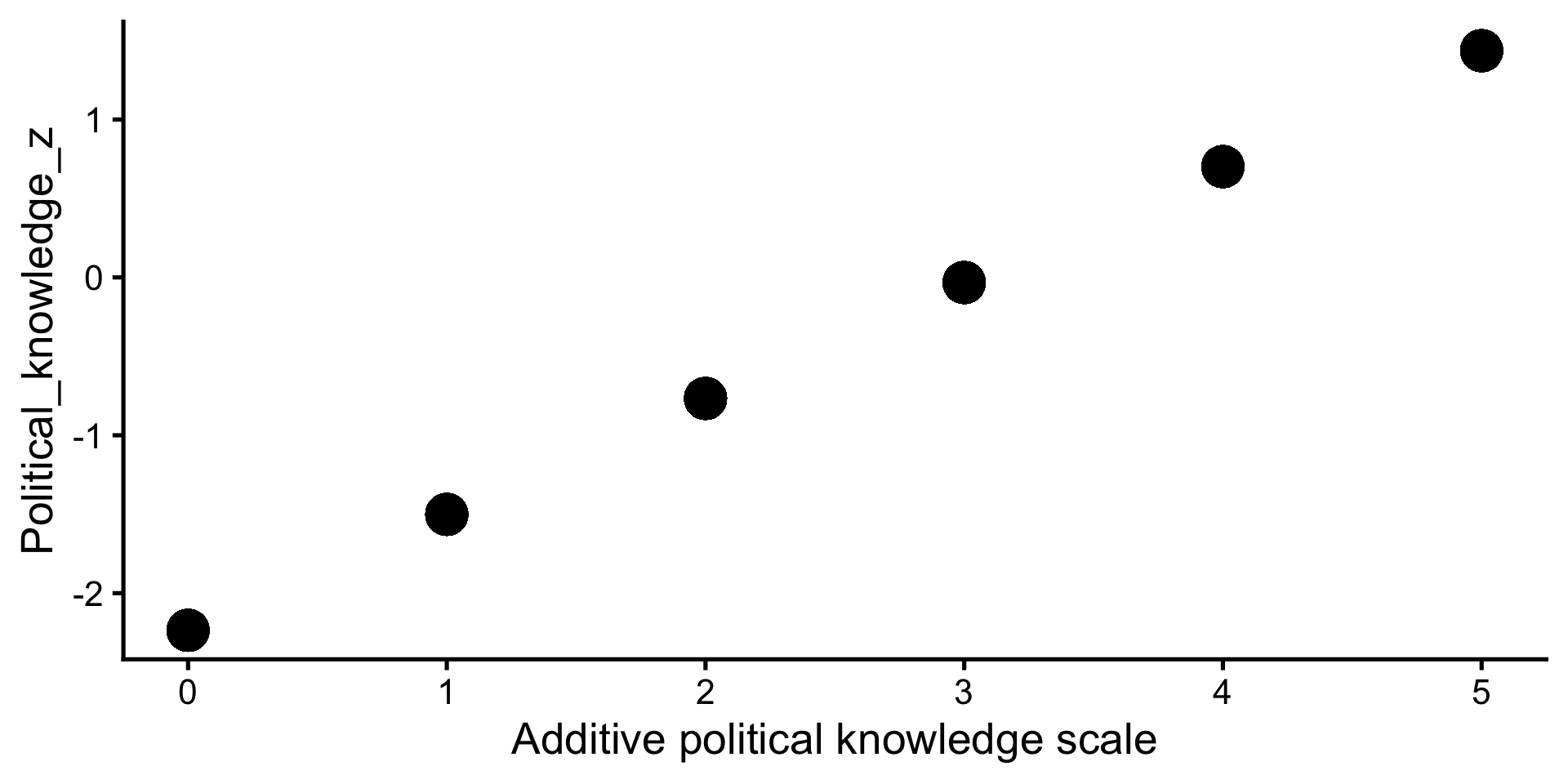
Multiplizieren & Dividieren mit einer Konst.
Original
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 1.48 | (1.16, 1.79) | 9.12 | < .001 | |
| Age | 0.03 | (0.02, 0.04) | 10.02 | < .001 | |
| R2 | 0.09 |
Z-Standardisiert
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 0.00 | (-0.06, 0.06) | 0.00 | > .999 | |
| Age z | 0.30 | (0.24, 0.36) | 10.02 | < .001 | |
| R2 | 0.09 |
Multiplizieren & Dividieren mit einer Konst.
| Parameter | Coefficient | 95% CI | t(991) | p | Std. Coef. | Std. Coef. 95% CI | Fit |
|---|---|---|---|---|---|---|---|
| (Intercept) | 1.48 | (1.16, 1.79) | 9.12 | < .001 | 0.00 | (-0.06, 0.06) | |
| Age | 0.03 | (0.02, 0.04) | 10.02 | < .001 | 0.30 | (0.24, 0.36) | |
| R2 | 0.09 |
- Die Funktion
report_table()schätzt das Modell im Hintergrund mit standardisierten quasi-metrischen Variablen neu, um die standardisierten Koeffizienten zu erhalten.
Nicht-lineare Transformationen
- z.B. Logarithmierung: Vergleich bzw. Veränderung in %
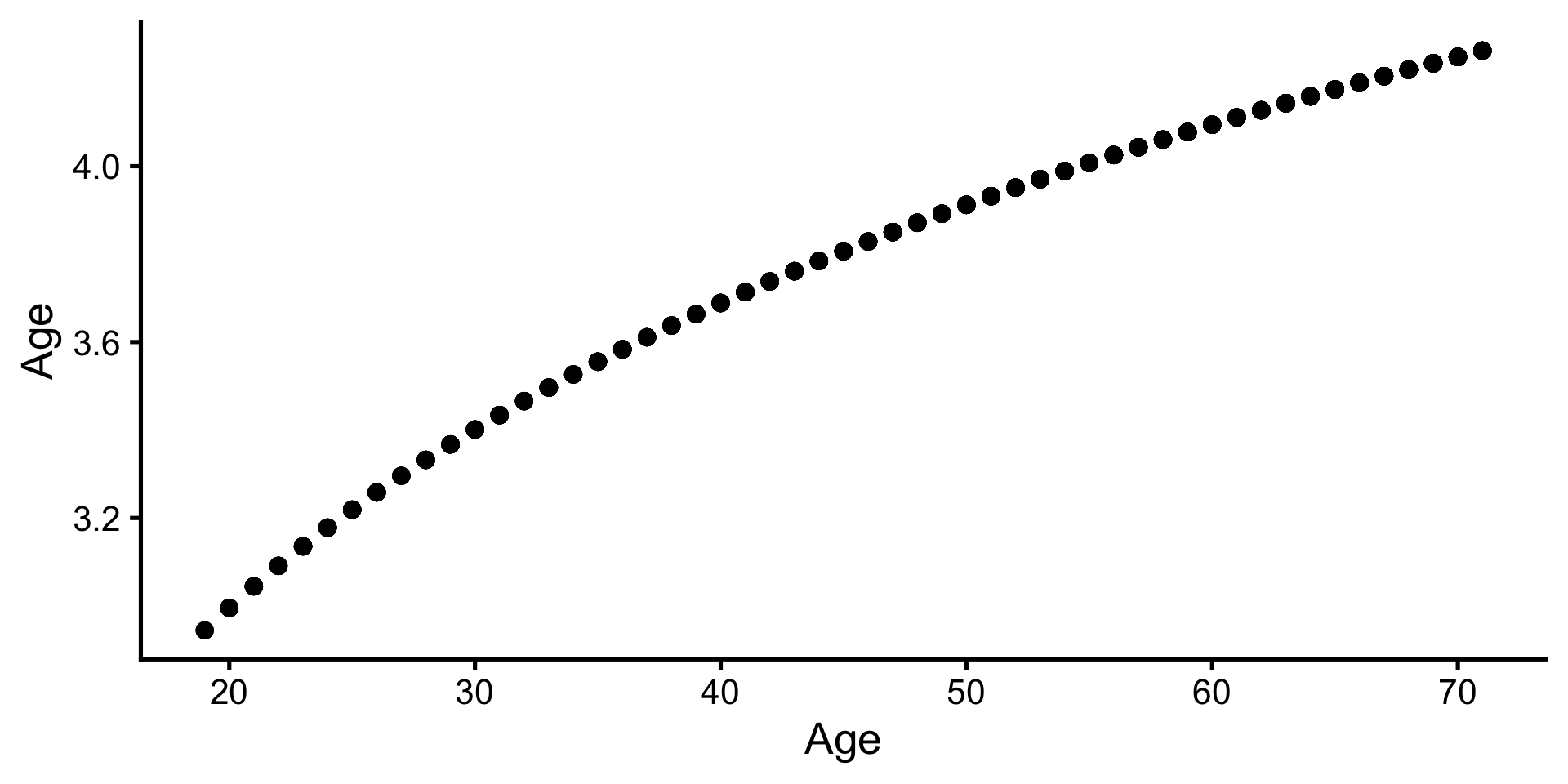
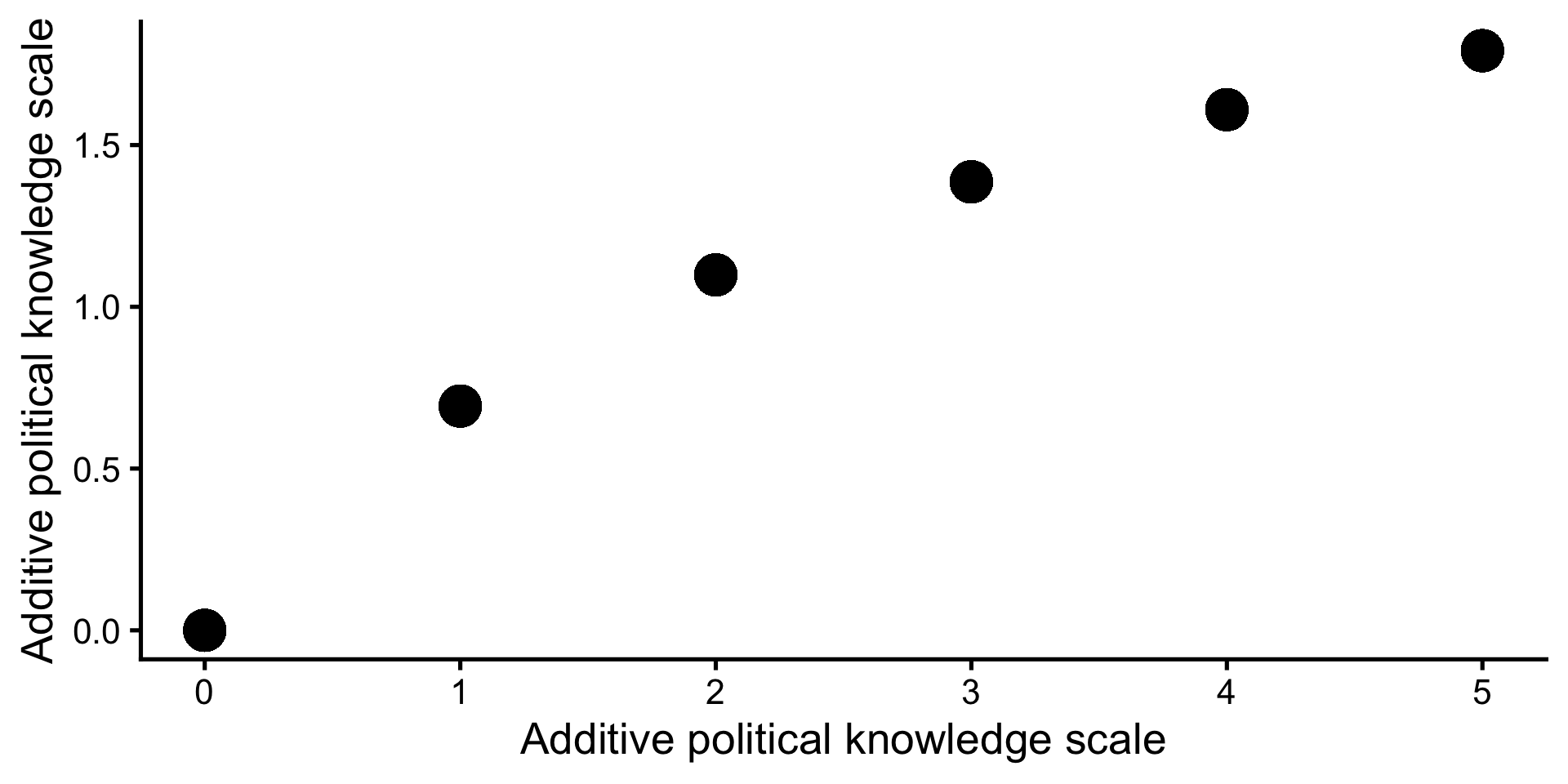
Nicht-lineare Transformationen
Original
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | 1.48 | (1.16, 1.79) | 9.12 | < .001 | |
| Age | 0.03 | (0.02, 0.04) | 10.02 | < .001 | |
| R2 | 0.09 |
Log-transformierte Variablen
| Parameter | Coefficient | 95% CI | t(991) | p | Fit |
|---|---|---|---|---|---|
| (Intercept) | -0.38 | (-0.70, -0.06) | -2.31 | 0.021 | |
| Age log | 0.43 | (0.35, 0.51) | 10.41 | < .001 | |
| R2 | 0.10 |
- log-log: Eine um 1% ältere Person beantwortet 0.43% mehr Fragen korrekt als eine um 1% jüngere Person (Oder ganz genau: liegt auf der Variable “Richtig beantwortete Fragen + 1” um 0.31% höher).
- Daumenregel für 100%: Eine doppelt so alte Person beantwortet ca. 43% mehr Fragen korrekt.
- Genauer gerechnet: Eine doppelt so alte Person beantwortet ca. \(2^{0.43} - 1 = 35\%\) mehr Fragen korrekt.
Fragen?
Zusammenfassung
Zusammenfassung
Mit der linearen Regression und ihren Varianten können wir sehr viele Fragen beantworten.
Grundgedanke immer: Wir legen Linien durch die Daten; die Steigung der Linien quantifiziert den Zusammenhang.
Abschnitt Grundlagen der Regression ist Voraussetzung für mindestens 2/3 der folgenden Inhalte.
Abschnitte Annahmen und ihre Überprüfung und Transformation von Variablen sind nützlich, aber nicht essentiell.
Übungsaufgaben
Fragen?
Nächste Einheit
Multiple lineare Regression
Danke — bis zur nächsten Sitzung.
Marko Bachl