

Das Laufzeitverfahren zur Effektivzinsberechnung


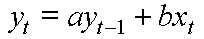
mit dem speziellen Problem der Effektivzinsberechnung innerhalb der Finanzmathematik.
a := q = Wachstumsrate (=1+p, p = Zinssatz) b := r = regelmäßige Zahlung y[t] := K[t] = Kapital nach t Perioden T := n = Laufzeit y[0] :=-s = Startwert (< 0, entsprechend dem Kreditvolumen) y[T] := 0 = Endsaldo
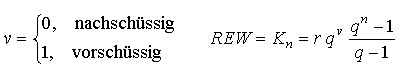
Gesucht ist also die Lösung der Gleichung
T
v q -1 T
r q ---- - s q = 0
q -1
Beispiel: Effektivzins
Ein Darlehen von 10 000 DM soll innerhalb von 6 Jahren zurückgezahlt werden. Folgende Fälle sind zu untersuchen: (a) am Anfang jedes Jahres (= vorschüssig) 2400 DM, (b) am Anfang jeden Monats (= vorschüssig) 200 DM, (c) am Ende jeden Monats (= nachschüssig) 200 DM. Ermitteln Sie den Effektivzinssatz. Zahlenwerte zu (a): b := r = 2400 v = 1 T := n = 6 y[0] :=-s = - 10 000 y[T] := 0 = EndsaldoDie Auflösung nach q ist i.a. nicht durch Angabe einer geschlossenen Formel möglich. Das Problem der Effektivzinsberechnung besteht gerade darin, den Wert q so zu wählen, daß zu vorgegebenen Werten für die Rate r und die Laufzeit n ein ebenfalls vorgegebener Sollwert REW erzielt wird.
Ein Verfahren, das wir als Laufzeitanpassungsverfahren - kurz: Laufzeitverfahren - bezeichnen wollen, geht problemorientiert von der Frage aus, ob sich nicht sämtliche Raten durch einen einmaligen Betrag in Höhe der Gesamtsumme ersetzen lassen, der dann als einmalige Zahlung mit einer bestimmten (virtuellen) Laufzeit zu verzinsen ist. Anschaulich könnte man zunächst die Hälfte der ursprünglichen Laufzeit ansetzen.
Bezeichnen wir die unbekannte Laufzeit mit x, so können wir unseren Näherungsansatz präzisieren (bei vorschüssiger Zahlung):j
T
q -1 x
rq ---- = rT q (vorschüssig)
q -1
Lösen wir diesen Ansatz nach x auf und betrachten wir anschließend den Grenzwert q->1, so erhalten wir als erste Näherung
T
1 q(q -1)
x = ---- ln ------- -> x = (T+1)/2
ln q (q-1)T
Im nachhinein ist diese Lösung auch anschaulich plausibel, da bei der vorschüssigen Verzinsung die längste Laufzeit T ist und die kürzeste Eins.x = (T-1)/2.
Setzen wir diese Approximation in unsere Ausgangsgleichung ein, so erhalten wir (vorschüssig)
(T+1)/2 T
rT q - s q = 0
und daraus zum ersten Mal eine brauchbare Näherungslösung für q:
2/(T-1)
q = (rT/s) (vorschüssig)
2/(T+1)
q = (rT/s) (nachschüssig)
allgemein:
2/(T+1-2v)
q = (rT/s) (nachschüssig: v=0, vorschüssig: v=1)
Das Zahlenbeispiel liefert folgende Näherungslösungen für q:
-----------------------------------------------------
jährlich Zins p.a. monatlich Zins p.a.
-----------------------------------------------------
nachschüssig 1.1098 10.98% 1.01004 12.74%
vorschüssig 1.1570 15.70% 1.01032 13.12%
-----------------------------------------------------
Die Brauchbarkeit der Näherungslösungen läßt sich bisher nur vorläufig anhand der Grafik beurteilen, für die eine vorschüssige Verzinsung vorausgesetzt wurde. Dabei ist zu beachten, daß die Formel nur für ganzzahlige Werte von t gilt.
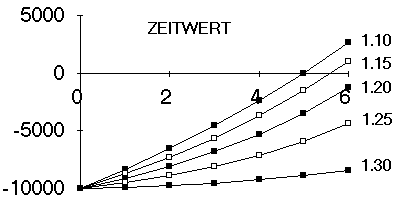
Hätten wir bereits den exakten Wert für q, so könnten wir eine äquivalente Laufzeit angeben, in der eine einmalige Zahlung des Gesamtbetrages denselben Wert liefert wie die Ratenzahlungen, nämlich
T
1 v q - 1 0, nachschüssig
x = ---- ln (q ------) mit v =
ln q (q-1)T 1, vorschüssig
Tatsächlich erhalten wir so nur eine dem angenäherten q-Wert äquivalente Laufzeit. Mit dieser besser angepaßten Laufzeit können wir jedoch aus
x T
rT q - s q = 0
einen neuen q-Wert ermitteln:
1/(T-x)
q = (rT/s)
------------------------------------
x[1] = (T-1+2v)/2
1/(T-x[i])
q[i] = (rT/s)
T
1 v q[i] - 1
x[i+1] = ------ ln (q[i] ---------)
ln q[i] (q[i]-1)T
0, nachschüssig
v =
1, vorschüssig
------------------------------------
-----------------------------------------------------
jährlich Zins p.a. monatlich Zins p.a.
-----------------------------------------------------
nachschüssig 1.1098 10.98% 1.01004 12.74%
1.1151 11.51% 1.01067 13.59%
1.1153 11.53% 1.01071 13.64%
1.1153 11.53% 1.01072 13.65%
vorschüssig 1.1570 15.70% 1.01032 13.12%
1.1727 17.27% 1.01101 14.05%
1.1743 17.43% 1.01106 14.11%
1.1745 17.45% 1.01107 14.12%
-----------------------------------------------------