Finanzmathematik

Ausgangspunkt ist das dynamisch-rekursives Basismodell S1000

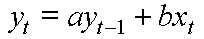
a    := q    = Wachstumsrate (=1+p, p = Zinssatz > 0)
b    := r    = regelmäßige Zahlung
x[t] := 1    = Faktor der regelmäßigen Zahlung
y[t] := K[t] = Kapital nach t Perioden
T    := n    = Laufzeit

1. Einmalige Zahlung

b=0

2. Regelmäßige Zahlung

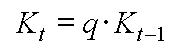
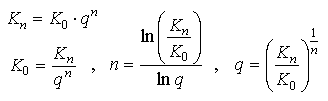
y[0] := K[0] = 0
y[T] := K[n] = REW = Rentenendwert

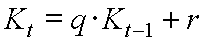
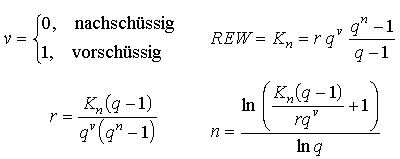
Bisher wurde nur die nachschüssige Zahlung beschrieben. Die vorschüssige Zahlung entspricht einer nachschüssige Zahlung einer einmal verzinsten Rate r'=rq. Mit Hilfe der zweiwertigen Variablen v lassen sich beide Fälle zusammen behandeln.

Die Auflösung nach q ist i.a. nicht durch Angabe einer geschlossenen Formel möglich. Das Problem der Effektivzinsberechnung besteht gerade darin, den Wert q so zu wählen, daß zu vorgegebenen Werten für die Rate r und die Laufzeit n ein ebenfalls vorgegebener Sollwert REW erzielt wird.

Das Problem der Effektivzinsberechnung läßt sich innerhalb der SPM-Systematik als Identifikationsproblem (P0) einordnen. Als zu identifizierenden Parameter kommen r und q in Frage.

Die Ermittlung der Laufzeit n entspricht der Zielsuche (P2) bzw. der Inversion (P3), je nachdem ob man eine numerische oder eine allgemeine Lösung anstrebt. Hierbei ist zu beachten, daß die oben angegebene Lösung genaugenommen nur für ganzzahlige Werte von n gilt.

Beispiel: Restschuld

Zur Baufinanzierung wird ein Kredit von 100 000 DM aufgenommen.
Am Anfang jeden Monats werden 2000 DM zurückgezahlt.
Es wird ein jährlicher Zinssatz von 12% zugrundegelegt.

(a) Berechnen Sie die Restschuld nach 3 Jahren.
(b) Wie hoch muß die monatliche Rate gewählt werden, wenn die
    Restschuld nach 3 Jahren höchstens 80 000 DM betragen soll?
(c) Nach welcher Zeit ist bei einer Monatsrate von 2000 DM die Restschuld
    erstmals unter 50 000 DM?
(d) Welchem Effektivzinssatz entspricht eine Restschuld von 70 000 DM?