S1000: Das dynamisch-rekursive Basismodell

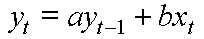
Spezialfälle:

a=1:             y[t] =   y[t-1] + b x[t]
b=0:             y[t] = a y[t-1]          ("Einmalige Zahlung")
x[t]=1:          y[t] = a y[t-1] + b      ("Auch regelmäßige Zahlung")
x[t]=1, y[0]=0:  y[t] = a y[t-1] + b      ("Regelmäßige Zahlung, nachschüssig")

Mit diesem Modell lassen sich typische Probleme der Finanzmathematik beschreiben.

Probleme:

(P0) Identifikation: Ermittlung von a und b
(P1) Enumeration: Ermittlung der "finalen Form":

(P2) Zielsuche:

 (1) Rückschluß: geg. x[1],..,x[T], y[T], ges. y[0]
 (2) Planung:    geg. y[0],..,y[T],       ges. x[1],..,x[T]

(P3) Inversion: wie (P2), aber mit variablen Sollwerten

Beispiel 1: Zinsrechnung, einmalige Zahlung

a    = Wachstumsrate (p=Zinssatz, a=1+p)
b    = 0
y[0] = Anfangskapital
T    = Laufzeit

y[T] = y[0] a^T

Beispiel 2: Zinsrechnung, regelmäßige Zahlung, nachschüssig

a    = Wachstumsrate (p=Zinssatz, a=1+p)
b    = regelmäßige Zahlung
y[0] = 0
T    = Laufzeit

y[T] = b (a^T - 1)/(a-1)  (a ≠ 1)