S1100: Das stochastische dynamisch-rekursive Modell

(univariat, linear)

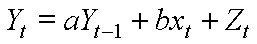
Erwartungswert y[t] = Erw(Y[t]):
y[t] = a y[t-1] + b x[t]  (vgl. S1000)

a=1:         Y[t] =   Y[t-1] + b x[t] + Z[t]
b=0:         Y[t] = a Y[t-1] + Z[t]
a=1, b=0:    Y[t] =   Y[t-1] + Z[t]
Random Walk: Y[t] =   Y[t-1] + Z[t]  mit Z[t] = ± 1

(P0) Identifikation: Ermittlung von a, b, Var(Z)
(P1) Enumeration: Finale Form
 
(P2) Zielsuche: z.B. Sollwert E(Y[T]) = y  numerisch vorgegeben (final value control problem)
 (1) open loop control:   x[t] nur von Y[0] abhängig
 (2) closed loop control: x[t] von den Realisationen von Y[0],..,Y[t-1] abhängig
(P3) Inversion: wie (P2), aber mit variablen Sollwerten
(P4) Optimierung: Optimale Steuerung,
z.B. Zielfunktion = quadratische Funktion der Abweichungen von Sollwerten

Methoden: Lagrange, Maximum-Prinzip, Dynamische Programmierung

Y[t] = Y[t-1] + x[t] - Z[t]