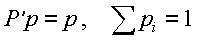Markoffketten


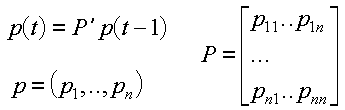
Markoffketten lassen sich mathematisch wie ein Spezialfall des multivariaten dynamisch-rekursiven Modells S1001 behandeln:
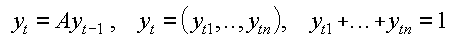
wobei anstelle von y[t] die Zustandswahrscheinlichkeiten treten und A durch die Transponierte der Übergangsmatrix ersetzt wird.
Hauptproblem ist dabei die Enumeration (P1), insbesondere das Grenzverhalten für t->unendlich. Bei absorbierenden Markoffketten interessieren die Absorptionswahrscheinlichkeiten und Absorptionszeiten, bei irreduziblen ergodischen (regulären) Markoffketten die stationären Wahrscheinlichkeiten.
E = Einheitsmatrix
N = Fundamentalmatrix,
n[i,j] = Erwartungswert der Häufigkeit des Zustandes j bei Start i (i,j transiente Zustände)
Z(j) = Häufigkeit des Zustandes j (abhängig vom Startzustand i)
N[dg] = Nullsetzen aller Elemente außerhalb der Diagonalen
N[sq] = Quadrieren sämtlicher Elemente von N
tau[sq]= Quadrieren sämtilcher Elemente von tau
T = Anzahl Schritte (einschl. Anfangszustand), in denen die MK in einem transienten Zustand ist
= Anzahl Schritte, um eine ergodische Menge zu erreichen
= Absorptionszeit bei absorbierenden MK (abhängig vom Startzustand i)
b[i,j] = Wahrscheinlichkeit für Absorption im Zustand j bei Start i (i transient)
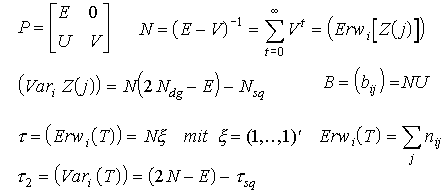
Beispiel: Absorbierende Markoffkette
1 0 0 0 0
0 1 0 0 0
P = q 0 0 p 0
0 0 q 0 p
0 p 0 q 0 (0 < p < 1, q = 1-p)
Für jede Anfangsverteilung p(0) konvergiert p(n) gegen die stationäre Verteilung p = (p1,..,pn). Sie läßt sich eindeutig bestimmen aus