S0101: Das multivariate stochastische Modell

(linear, statisch)

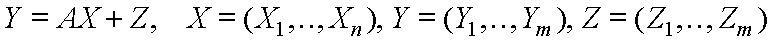
Spezialfall:

Y = a1 X1 + a2 X2 + Z

(P0) Identifikation: Schätzen der Parameter, z.B.
a1, a2, Var(Z): multiple lineare Regression

(P1) Enumeration: Ermittlung der Verteilung von Y
 (1) zu gegebener Verteilung von X
 (2) zu gegebenem x = (x1,...,xn)

(P2) Zielsuche: Ermittlung von x=(x1,...,xn) zu numerisch vorgegebenem y=(y1,...,yn)
 (1) Rückschluß: Posterior-Verteilung
 (2) Planung: Maximum-Likelihood-Methode
Der Unterschied zwischen Rückschluß und Planung wurde bereits beim stochastischen Basismodell S0100 behandelt.

(P3) Inversion: wie (P2), nur y als Variable behandelt. 
(P4) Optimierung

X[t] = a1 X[t-1] + a2 X[t-2] + Z[t]

Dieses Beispiel des autoregressiven Schemas zweiter Ordnung läßt sich nicht genau in das hier behandelte
statische Modell einordnen. Setzt man jedoch im oben angegebenen Spezialfall

Y    = X[t]
X[1] = X[t-1]
X[2] = X[t-2],

so lassen sich einige Ergebnisse übertragen.