S0100: Das stochastische Basismodell

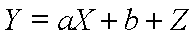
Version 2 (Einflußgröße x einstellbar):

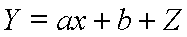
Spezialfälle:

Y = X + Z  (Version 1)
Y = x + Z  (Version 2)

(P0) Identifikation:

Lineare Regression: Schätzen von a, b und V(Z) aus einer Stichprobe (X1,Y1),..,(Xn,Yn) bzw. (x1,Y1),..,(xn,Yn);
vgl. multivariates nichtlineares Modell (S0011), Optimierung (P4), geschlossene Lösung (M1)

(P1) Enumeration:

Ermittlung der (bedingten) Verteilung von Y zu gegebener Verteilung von X bzw. zu gegebenem x.
Normalverteilung:


(P2/P3) Zielsuche/Inversion:

Ermittlung von x0 zu vorgegebenem Y=y0

 (Version 1) Rückschluß: Posterior-Verteilung
 (Version 2) Planung:    Likelihood-Funktion

Bei Version 2 ist die Einflußgröße einstellbar. Zielsuche und Inversion beziehen sich auf die Ermittlung dieser Variablen. Dies ist ein Planungsproblem. Eine angemessene Lösung besteht darin, denjenigen Wert zu finden, der den Sollwert mit maximaler Wahrscheinlichkeit realisiert (Maximum-Likelihood-Methode).

Beispiel: Rückschluß und Planung (Würfelmodell)

Wir verwenden zunächst zwei Würfel und bezeichnen mit X die Augenzahl 
des ersten Würfels und mit Y die Würfelsumme. Dann ist der Zusammenhang 
zwischen den beiden Zufallsvariablen X und Y über die weitere 
Zufallsvariable Z (= Augenzahl des zweiten Würfels) vermittelt: Y = X + Z .

Nehmen wir nun an, daß für die Würfelsumme der Wert Y=10 vorgegeben ist, so 
stellen sich in diesem stochastischen Modell die beiden Fragen:

(1) Rückschluß: Welche Augenzahl stammt vom ersten Würfel?
                Genauer: Für welche Augenzahl ergibt sich eine maximale 
                Wahrscheinlichkeit?
(2) Planung:    Welche Augenzahl sollte man für den ersten Würfel wählen, 
                um die Würfelsumme Y=10 mit möglichst großer 
                Wahrscheinlichkeit zu erzielen?

In beiden Aufgabenstellungen kommen für X die Werte 4, 5 und 6 in Frage. 
Für den Rückschluß ist die Aposteriori-Wahrscheinlichkeit W(X=x / Y=10) 
maßgeblich, die jeweils den Wert 1/3 hat. Für die Planung ist die 
Likelihood-Funktion W(Y=10 / X=x) maßgeblich, die jeweils den Wert 1/6 hat.

In diesem einfachen Beispiel sind daher alle drei Werte für X gleichwertig 
und zwar sowohl beim Rückschluß als auch bei der Planung. Man muß hier 
nicht zwischen den beiden Aufgabenstellungen unterscheiden. Der Grund liegt 
darin, daß als Apriori-Verteilung eine Gleichverteilung vorliegt. Die 
Bayes-Formel liefert dann sofort das Ergebnis, daß sich die Aposteriori-
Verteilung und die Likelihood-Funktion nur durch eine Konstante 
unterscheiden, beide Funktionen also an denselben Stellen Maximalwerte 
haben.

Wählt man für X und Z jeweils die Würfelsumme aus zwei Würfeln, gibt also 
für Y die Augenzahl aus vier Würfeln vor (Y=22), so erhält man i.a. 
unterschiedliche Optimalwerte für Rückschluß (X=11) und Planung (X=12).

Das Ergebnis ist insofern bemerkenswert, als in der klassischen Statistik 
die Maximum-Likelihood-Methode stets als elegantes Verfahren auch und 
gerade für den Rückschluß (insbesondere für die Punktschätzung) gepriesen 
wird.