Refereed papers, invited reviews
|
 |
 |
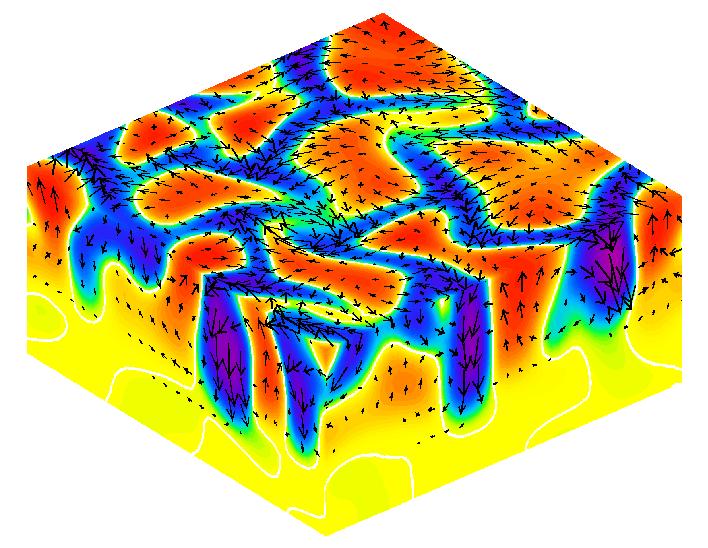
Snapshot of the flow (u). The vertical velocity is indicated by
the coloring (red: upward, blue: downward), the direction of the flow by the arrows. |
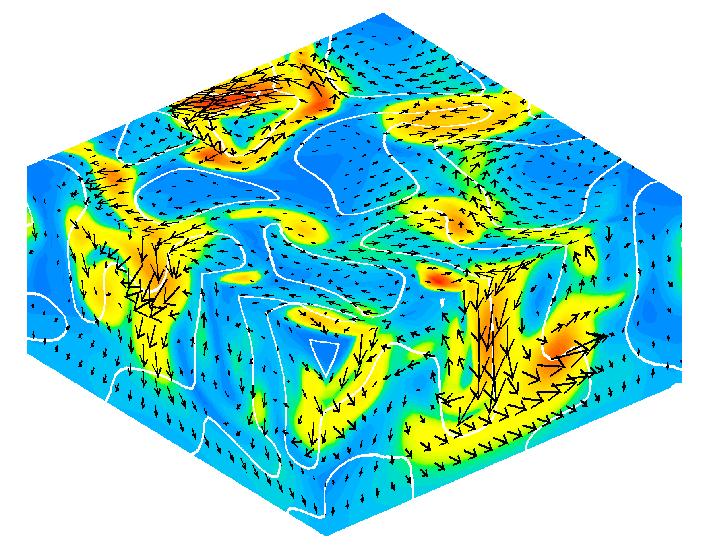
Simultaneous snapshot of the magnetic field (B). The strength of the magnetic field is indicated
by the coloring (blue: low, red: high), and its orientation by the arrows.
The white curve denotes the zero level of the vertical velocity. |
3D simulation of solar magnetoconvection
The large-scale magnetic field of the Sun is produced by dynamo action in the convection zone.
In order to understand the dynamo process, knowledge of the dynamo coefficients is crucial.
By means of 3D magnetohydrodynamic (MHD) simulations, these are calculated
from the electromotive force, uxb, where u and b are the disturbances of the
velocity and the magnetic field, respectively. The simulation domain shown here
represents a section of the solar convection zone,
sandwiched between a thin cooling layer on top and a stably stratified layer underneath. From
below the box is supplied with a constant heat flux; at the top the
temperature is held fixed. The axis of rotation points downward, as
is the case on the south pole of the Sun. Initially, the magnetic
field is vertical and homogeneous. |
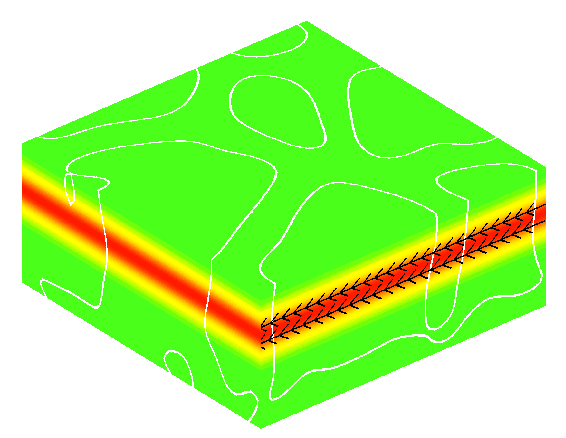 |
Turbulent diffusion and magnetic pumping in 3D magnetoconvection |
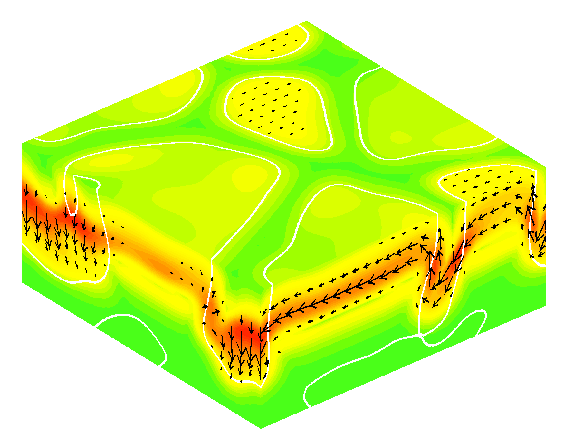 |
Three snapshots of the magnetic field (B).
The strength of the magnetic field is indicated by the coloring (green: low, red: high), and its orientation by the arrows.
The white curve denotes the zero level of the vertical velocity. It separates isolated upwelling regions from
downflowing lanes. Initially, a weak magnetic field with a horizontal orientation and a Gaussian dependence on depth is
introduced into the middle of the convectively unstable layer. Subsequently, this layer is modified by advection.
|
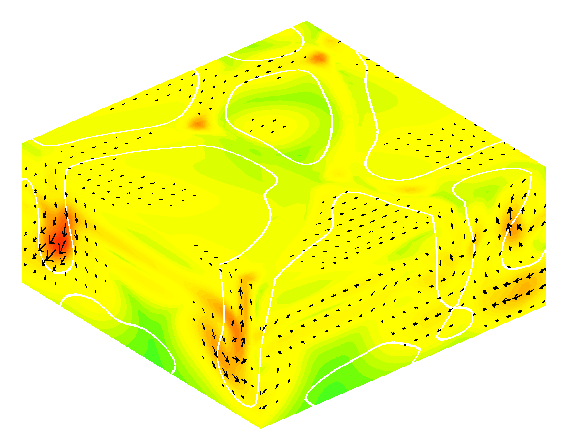 |
On average, this results in a spreading of the magnetic field equivalent to turbulent diffusion as well as a net downward
advection that can be attributed to magnetic pumping. |