Kausalinferenz

Methoden der empirischen Kommunikations- und Medienforschung

Marko Bachl

Freie Universität Berlin

Mehr Webtracking?

Workshop: Web Tracking: From Raw Data to Analysis

Zeit und Ort: 12. & 13. Februar, ca. 9-16 Uhr, Garystr. 55

Dozent: Dr. Frank Mangold (GESIS)

Anmeldung: 23. Januar. Noch einzelne Plätze verfügbar.

Inhalt: The Internet has profoundly reshaped everyday life and media use. Traditional self-reports reach their limits when capturing the diversity and dynamics of digital behavior. Web tracking offers a behaviorally grounded approach—especially in combination with panel surveys. At the same time, such data pose theoretical, infrastructural, ethical, and legal challenges. This workshop provides a practice-oriented introduction to preprocessing and analyzing web-tracking data, highlights typical decision points (“researcher degrees of freedom”) and best practices, and—together with participants—develops suitable research designs in Computational Communication Research. Alongside conceptual and methodological input, hands-on exercises with example datasets in R are a central focus.

Alle Informationen und Link zur Anmeldung

Alle Informationen und Link zur Anmeldung

Kausalinferenz

Mit Material von Dr. Julia M. Rohrer, Universität Leipzig. Originale hier

Agenda

  1. Einführung
  2. Potential Outcomes und randomisierte Experimente
  3. Fundamentale kausale Strukturen
  4. Fazit

Einführung

Korrelation \(\neq\) Kausalität - oder doch?

xkcd

Warum empirische Analysen?

  • Beschreibung (description)
    • Wie lange nutzen Jugendliche welche Social-Media-Plattformen und mit welchen soziodemographischen Eigenschaften hängt die Nutzung zusammen?
    • Wie unterscheiden sich die öffentlich sichtbaren Reaktionen auf Posts von Parteien und Politiker:innen nach Parteizugehörigkeit und Inhalt?
  • Vorhersage (prediction)
    • Wie gut lässt sich das zukünftige Wohlbefinden (z.B. am nächsten Tag) aus den Social-Media-Aktivitäten vorhersagen?
    • Wie gut lassen sich die Wahlergebnisse aus öffentlich sichtbaren Reaktionen auf Posts von Parteien und Politiker:innen vorhersagen?
  • Kausalinferenz (causal inference, counterfactual prediction)
    • Führt eine Reduktion der Social-Media-Nutzung zu höherem Wohlbefinden?
    • Führt eine größere TikTok-Nutzung vor der Wahl zu einer höheren Wahrscheinlichkeit, bestimmte Parteien zu wählen?

2 Arten von kausalen Fragen

Rückwärts gerichtet

  • Warum ist die Welt so, wie sie ist?
    • Warum haben Jugendliche niedriges Wohlbefinden oder psychische Probleme?
    • Warum wählen junge Wähler:innen die AfD?



  • causes of effects, Ursachen von Wirkungen bzw. ihrer Konsequenzen
  • allgemeine (“große”) Fragen, zu deren Beantwortung die gesammelte Studienlage beitragen kann

Vorwärts gerichtet

  • Wie würde sich die Welt verändern, wenn wir eine bestimmte Intervention vornehmen (könnten)?
    • Wie verändert sich das Wohlbefinden, wenn wir die Social-Media-Nutzung reduzieren?
    • Wie verändert sich die Wahlwahrscheinlichkeit für die AfD, wenn wir die TikTok-Nutzung reduzieren?

  • effects of causes, Wirkungen bestimmter Ursachen
  • konkrete (“kleine”) Fragen, die wir in einzelnen Studien zu beantworten versuchen
  • (Die effects of causes der Medienwirkungsforschung decken nur einen [kleinen] Ausschnitt aller causes of effects ab. Es gibt viele Gründe für die Sorgen und Wahlentscheidungen junger Menschen — nicht nur Social Media.)

Fragen?

Definition

Potential Outcomes (PO)

POFlow Aufwachen Aufwachen SMFrage Instagram checken? Aufwachen->SMFrage WohlbefindenJa Wohlbefinden nach Instagram SMFrage->WohlbefindenJa Ja WohlbefindenNein Wohlbefinden ohne Instagram SMFrage->WohlbefindenNein Nein


  • Kausaler Effekt: Vergleich der beiden möglichen Zustände der Welt
  • Unabhängige Variable \(X\) (uV, Treatment, Exposure, Experimentalgruppe, …)
  • \(X = 0\): kein Instagram; \(X = 1\): Instagram
  • Abhängige Variable \(Y\) (auch. aV, Outcome, Kriterium, …)
  • \(Y = 0\): niedriges Wohlbefinden; \(Y = 1\): hohes Wohlbefinden
  • Potential Outcomes \(Y^X\)
  • \(Y^{X=0}\) oder \(Y^0\): Wohlbefinden, wenn Instagram nicht gecheckt wurde
  • \(Y^{X=1}\) oder \(Y^1\): Wohlbefinden, wenn Instagram gecheckt wurde

Definition kausaler Effekte im PO-Framework

  • Individueller kausaler Effekt: \(Y^1 - Y^0\)
  • Der kausale Effekt des Checkens von Instagram auf das Wohlbefinden einer Person ist die Differenz zwischen dem Wohlbefinden wenn die Person Instagram gecheckt hat und ihrem Wohlbefinden wenn sie Instagram nicht gecheckt hat.
  • Problem: In jeder realen Situation hat die Person entweder Instagram gecheckt oder nicht gecheckt.
  • Eines der beiden Potential Outcomes wird realisiert (beobachtbar)
  • Das andere Potential Outcome ist ein Counterfactual (nicht beobachtbar)

Definition kausaler Effekte im PO-Framework

Person X Y Y0 Y1 Y1 - Y0
Maximiliane 1 0 ? 0 ???
  • Fundamentales Problem der kausalen Inferenz: Wir beobachten immer nur eines der Potential Outcomes, somit ist es unmöglich den individuellen kausalen Effekt zu berechnen
  • Kausale Identifikation (= erfassbar, schätzbar machen) durch Designs, Analysen und Annahmen

Randomisiertes Experiment

Person X Y Y0 Y1 Y1 - Y0
Maximiliane 1 0 ? 0 ???
Daniel 0 1 1 ? ???
Joséphine 0 1 1 ? ???
Charlotte 1 1 ? 1 ???
Melanie 0 0 0 ? ???
Leyla 1 0 ? 0 ???
Celina 0 1 1 ? ???
  • X wird zufällig zugewiesen, z.B. Rezeptionsaufforderung im Labor

Randomisiertes Experiment

\[E[Y^1 - Y^0] = \] \(E[]\) = Erwartungswert
\[= E[Y^1] - E[Y^0] =\] Linearität des Erwartungswerts
\[= E[Y^1 \mid X = 1] - E[Y^0 \mid X = 0] =\] Da \(X\) zufällig zugeteilt wurde (Randomisierung), ist \(X\) unabhängig von den Potential Outcomes:
\(E[Y^1] = E[Y^1 \mid X = 0] = E[Y^1 \mid X = 1]\)
\(E[Y^0] = E[Y^0 \mid X = 0] = E[Y^0 \mid X = 1]\)
\[ = E[Y \mid X = 1] - E[Y \mid X = 0]\] Konsistenzannahme: In den Gruppen werden die jeweils korrespondierenden Potential Outcomes beobachtet

Randomisiertes Experiment

Person X Y Y0 Y1 Y1 - Y0
Maximiliane 1 0 ? 0 ???
Daniel 0 1 1 ? ???
Joséphine 0 1 1 ? ???
Charlotte 1 1 ? 1 ???
Melanie 0 0 0 ? ???
Leyla 1 0 ? 0 ???
Celina 0 1 1 ? ???

\[ E[Y \mid X = 1] - E[Y \mid X = 0]\] \[ = (0+1+0)/3 - (1+1+0+1)/4 = \] \[ = 0.33 - 0.75 = \] \[ = -0.42\]

  • Durchschnittlicher kausaler Effekts des Instagram-Checkens
  • Average Treatment Effect (ATE)

Zwischenfazit

  • In einzelnen Studien betreiben wir vorwärts gerichtete Kausalinferenz. Wir schätzen den kausalen Effekt eines bestimmten Treatments.
  • Mit vielen Studien können wir rückwärts gerichtete Fragen beantworten. Wir sammeln die Gründe, warum die Welt so ist, wie sie ist.
  • Im Potential Outcomes Framework sind kausale Effekte definiert als Differenzen zwischen den unterschiedlichen Welten.
  • Das fundamentale Problem der Kausalinferenz ist, dass wir für eine Person und Situation immer nur eine Welt beobachten können. Die andere Welt bleibt ein Counterfactual.
  • In randomisierten Experimenten ist der Mittelwertsunterschied zwischen den Gruppen ein unverzerrter Schätzer des durchschnittlichen kausalen Effekts.

  • Aber was ist, wenn wir kein randomisertes Experiment durchführen können oder wollen?

Fragen?

Fundamentale kausale Strukturen

Minimale Annahmen für kausale Effekte

  • Zusammenhang: Es besteht nach angemessener Modellierung ein Zusammenhang zwischen uV und aV

  • Zeitliche Reihenfolge: uV liegt zeitlich vor aV

  • Keine plausiblen alternativen Erklärungen: alle und nur die relevanten Drittvariablen wurden gemessen und im Modell berücksichtigt

Randomisiertes Experiment

  • Zusammenhang: z.B. Regressionskoeffizient des Indikators für Experimentalgruppe vs. Kontrollgruppe

  • Zeitliche Reihenfolge: Erst Treatment, dann aV

  • Keine plausiblen alternativen Erklärungen: uV ist durch Design mit keinen anderen gemessenen oder nicht gemessenen Variablen korreliert; keine alternativen Erklärungen möglich

Nicht experimentelle Designs (?)

  • Zusammenhang: z.B. Koeffizient der uV aus multipler Regression

  • Zeitliche Reihenfolge: Längsschnitt oder Theorie

  • Keine plausiblen alternativen Erklärungen: Messen und Berücksichtigen aller wichtigen und richtigen Variablen im Regressionsmodell

  • Identifikation kausaler Effekte basiert größtenteils auf (nicht direkt testbaren) Annahmen → Theorie!

Variablen in kausalen Modellen

  • Variablen, für die wir uns interessieren
    • X: unabhängige Variable, von der ein kausaler Effekt ausgeht (auch uV, Treatment, Exposure, Experimentalgruppe, …)
    • Y: abhängige Variable, die von uV beeinflusst wird (auch. aV, Outcome, Kriterium, …)
    • Kausaler Effekt: X → Y
  • Fundamentale kausale Strukturen zwischen X und Y:
    • fork (Gabel): X ← Confounder → Y
    • chain (Kette): X → Mediator → Y
    • inverted fork (umgekehrte Gabel): X → Collider ← Y

Fork & Confounder

  • uV: unabhängige Variable, von der Effekt ausgeht
  • aV: abhängige Variable, die von uV beeinflusst wird
  • Confounder: Variable, die uV und aV beeinflusst.
  • Kausale Effekte des Confounder führen zu Zusammenhang zwischen uV und aV (sog. “Scheinkorrelation”)
  • Kontrolle des Confounder nötig, um beobachteten Zusammenhang zu entfernen (z.B. als Prädiktor in multipler Regression, Analyse nach Counfounder-Gruppen, Konstanthalten durch Stichprobenziehung)
  • Typisches Problem: Unbekannte oder nicht gemessene Confounder (“omitted variable bias”)

Wahres kausales Modell

G Confounder Confounder uV uV Confounder->uV aV aV Confounder->aV

Folgen bei falscher Spezifikation

G Confounder Confounder uV uV aV aV uV->aV

Fork & Confounder: Beispiel

Wahres kausales Modell

G Confounder Fehlende Freizeitangebote uV Social-Media-Nutzung Confounder->uV aV Wohlbefinden Confounder->aV

Folgen bei falscher Spezifikation

G Confounder Fehlende Freizeitangebote uV Social-Media-Nutzung aV Wohlbefinden uV->aV

Chain & Mediator

  • uV: unabhängige Variable, von der Effekt ausgeht
  • aV: abhängige Variable, die von uV beeinflusst wird
  • Mediator: Variable, die von uV beeinflusst wird und dann wiederum aV beeinflusst.
  • Kontrolle des Mediator nicht erlaubt, wenn wir gesamten kausalen Effekt von uV auf aV schätzen wollen.
  • Analyse mit Mediator manchmal gewünscht, wenn wir den Prozess uV → Mediator → aV untersuchen wollen (“indirekter Effekt”)
  • Typisches Problem: Kontrolle von Mediator unterschätzt den kausalen Effekt von uV und aV (“overcontrol/overadjustment bias”)

Interessanter kausaler Effekt

G uV uV aV aV uV->aV

Folgen bei unpassender Spezifikation

G Mediator Mediator aV aV Mediator->aV uV uV uV->Mediator uV->aV

Chain & Mediator: Beispiel

Interessanter kausaler Effekt

G uV Social-Media-Nutzung aV Wohlbefinden uV->aV

Folgen bei unpassender Spezifikation

G Mediator Online Social Support aV Wohlbefinden Mediator->aV uV Social-Media-Nutzung uV->Mediator uV->aV

Inverted Fork & Collider

  • uV: unabhängige Variable, von der Effekt ausgeht
  • aV: abhängige Variable, die von uV beeinflusst wird
  • Collider: Variable, die von uV und aV beeinflusst wird.
  • Kontrolle des Collider nicht erlaubt
  • Typisches Problem: Kontrolle (oder andere Berücksichtigung, z.B. Stichprobenziehung in Abhängigkeit des Colliders) von Collider führt zu beobachtetem Zusammenhang zwischen kausal unabhängigen uV und aV (“collider bias”)

Wahres kausales Modell

G Collider Collider uV uV uV->Collider aV aV aV->Collider

Folgen bei falscher Spezifikation

G Collider Collider aV aV Collider->aV uV uV uV->aV

Inverted Fork & Collider: Beispiel

Wahres kausales Modell

G Collider Schlafmangel uV Social-Media-Nutzung uV->Collider aV Wohlbefinden aV->Collider

Folgen bei falscher Spezifikation

G Collider Schlafmangel aV Wohlbefinden Collider->aV uV Social-Media-Nutzung uV->aV

Zwischenfazit

Wahrer kausaler Prozess Zusammenhang zwischen uV und uV ohne Kontrolle Zusammenhang zwischen uV und aV bei Kontrolle der mittleren Variable
aV ← Confounder → uV Nicht-kausaler Zusammenhang Kein Zusammenhang
uV → Mediator → aV Kausaler Zusammenhang Kein (oder geringerer) Zusammenhang
aV → Collider ← uV Kein Zusammenhang Nicht-kausaler Zusammenhang

Zwischenfazit

In der Praxis treten diese Strukturen oft gleichzeitig auf. Um den wahren Effekt zu identifizieren, müssen wir die Rolle jeder Variable theoretisch klären.

G uV Social-Media- Nutzung (uV) aV Wohlbefinden (aV) uV->aV   Direkter Effekt (?) Med Online Social Support (Mediator) uV->Med Coll Schlafmangel (Collider) uV->Coll aV->Coll Conf Fehlende Freizeitangebote (Confounder) Conf->uV Conf->aV Med->aV

Identifikation des Effekts:

Confounder: Muss kontrolliert werden, sonst erhalten wir nicht kausale Assoziation (omitted variable bias)

Mediator: Darf nicht kontrolliert werden, sonst blockieren wir den Wirkmechanismus (overcontrol/overcontrol bias)

Collider: Darf nicht kontrolliert werden (oder keine Auswahl nach Schlafmangel), sonst verzerren wir das Ergebnis (collider bias).

Noch immer massiv vereinfachtes Toy Example. Realität ist wesentlich komplexer!

Zwischenfazit

  • Die Spezifikation eines passenden Modells zur Identifikation eines kausalen Effekts erfordert starke, häufig vor allem theoretisch zu begründende Annahmen.
  • Falsche Spezifikation des kausalen Modells führt zu inhaltlich falschen Schlüssen. Ergebnisse eines Regressionsmodells beruhen auf der Annahme, dass das zugrunde liegendes Modell richtig abgebildet wurde.
  • Überspezifizierte “große” Regressionsmodelle mit möglichst vielen Kontrollvariablen (“um ganz sicher zu gehen habe ich alles denkbare kontrolliert”; a.k.a. “kitchen sink regression”, “causal salad”) ohne Nachdenken über kausale Annahmen
    • → Gefahr von Collider- und Mediator-Variablen im Modell
    • → “overcontrol/overadjustment bias”
  • Unterspezifizierte “sparsame” Regressionsmodelle mit nur wenigen Kontrollvariablen (“aber ich wollte es doch einfach und übersichtlich halten”) und ohne Identifikation durch Studiendesign
    • → Gefahr von fehlenden Confounder-Variablen im Modell
    • → “omitted variable bias”

Fazit: Es ist kompliziert

xkcd

Fazit: Es ist kompliziert

Aber aufgeben hilft auch nicht weiter.

  • Intelligente Experimentaldesigns wo möglich und aussagekräftig
  • Transparente Kommunikation der Annahmen zur Identifikation kausaler Effekte
  • Keine Lösung: Über Korrelationen schreiben, Kausalität implizieren (Grosz et al., 2020)

Fragen?

Lektüreempfehlungen

(Rohrer, 2018)

(Keele et al., 2020)

  • Rohrer (2018): Sehr gut lesbare Einführung

  • Keele et al. (2020): Direkte Anwendung auf die Auswahl von Variablen und die Interpretation von Regressionsmodellen

(in über diese Vorlesung hinausgehenden Inhalten nicht klausurrelevant)

Hausaufgabe

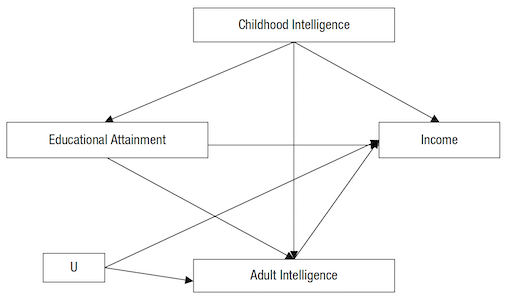
Kehren Sie mit Ihrem Wissen über Kausalinferenz zu Modell 4 in Van Erkel & Van Aelst (2021) zurück (z.B. hier). Beantworten Sie diese Fragen:

  • Wie beurteilen Sie die Studie und die Analyse insgesamt vor diesem Hintergrund?
  • Welche Koeffizienten würden Sie als kausale Effekte interpretieren?
  • Wie würden Sie das Modell verändern, um den Koeffizienten von Political Interest als kausalen Effekt zu interpretieren?
  • Würden Sie den Koeffizenten von Gender: Female kausal interpretieren? Warum (nicht)? Gäbe es ein Modell, in dem Sie das tun würden?

Nächste Einheit

Pfadmodelle & Mediation

Danke

Marko Bachl

Literatur

Cunningham, S. (2021). Causal inference: The mixtape. Yale University Press. https://mixtape.scunning.com/
Gelman, A., & Imbens, G. (2013). Why ask why? Forward causal inference and reverse causal questions. National Bureau of Economic Research. https://doi.org/10.3386/w19614
Grosz, M. P., Rohrer, J. M., & Thoemmes, F. (2020). The taboo against explicit causal inference in nonexperimental psychology. Perspectives on Psychological Science, 15(5), 1243–1255. https://doi.org/gg6p4f
Hernán, M. A., Hsu, J., & Healy, B. (2019). A second chance to get causal inference right: A classification of data science tasks. CHANCE, 32(1), 42–49. https://doi.org/gf6r2t
Keele, L., Stevenson, R. T., & Elwert, F. (2020). The causal interpretation of estimated associations in regression models. Political Science Research and Methods, 8(1), 1–13. https://doi.org/gf5sjg
Rohrer, J. M. (2018). Thinking clearly about correlations and causation: Graphical causal models for observational data. Advances in Methods and Practices in Psychological Science, 1(1), 27–42. https://doi.org/10.1177/2515245917745629
Van Erkel, P. F. A., & Van Aelst, P. (2021). Why don’t we learn from social media? Studying effects of and mechanisms behind social media news use on general surveillance political knowledge. Political Communication, 38(4), 407–425. https://doi.org/ghk94s