

S0011: Das multivariate nichtlineare Modell


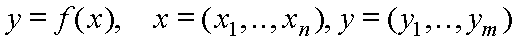
Spezialfälle:
m=1, n=2: y = f(x1,x2)
m=2, n=2: y1 = f1(x1,x2)
y2 = f2(x1,x2)
quadratisch: 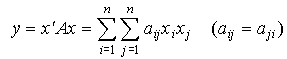
Probleme:
(P0) Identifikation: Ermittlung der Parameter (P1) Enumeration: Berechnung der Funktionswerte (P2) Zielsuche: Nichtlineare Gleichungssysteme, z.B. f1(x1,x2) = 0 f2(x1,x2) = 0 (P3) Inversion: Ermittlung von x zu beliebigem y i.a. nicht möglich, nur numerische Lösungen (P4) Optimierung: y = f(x) -> Max wird häufig auf das Lösen nichtlinearer Gleichungssysteme (P2) zurückgeführt: (1) ohne Nebenbedingung:Beispiel: Monopolist mit zwei Gütern(2) mit Nebenbedingung g(x1,x2)=0 (Lagrange):
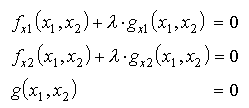
p[i] = Preis für Gut i x[i] = Absatz des Gutes i k[i] = Kosten einer Einheit des Gutes i U = Umsatz K = Gesamtkosten G = Gewinn x[1] = a[1,0] + a[1,1] p[1] + a[1,2] p[2] x[2] = a[2,0] + a[2,1] p[1] + a[2,2] p[2] U = p[1] x[1] + p[2] x[2] K = k[1] x[1] + k[2] x[2] G = U - K -> Max