S0001: Das multivariate Basismodell

Spezialfall: 2-mal-2-Matrix

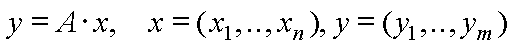
Probleme:

(P0) Identifikation: Ermittlung der Matrix A
(P1) Enumeration: Multiplikation des Vektors x (von links) mit der Matrix A.
(P2) Zielsuche: Lösung eines linearen Gleichungssystems
(P3) Inversion: Matrizeninversion

(P4) Optimierung: Lineare Optimierung

Beispiel: Diät

Ein Geflügelfarmer verfüttert zwei Sorten von Futter. Die Mischung enthält insbesondere Eiweiß und Kohlehydrate.

x1 = Menge der Sorte 1         y1 = Menge Eiweiß in der Mischung
x2 = Menge der Sorte 2         y2 = Menge Kohlehydrate in der Mischung

           x1      x2
     ----------------
     y1   0.2     0.5
     y2   0.1     0.3

z.B. sind also in einem kg der Sorte 1 genau 0.2 kg Eiweiß.

Beispiel zur Identifikation von Parametern (P0):

An dem folgenden Beispiel kann man sehen, daß die Identifikation (eines einzigen Parameters) bereits auf eine nichtlineare Gleichung führen kann, die sich nur numerisch lösen läßt:

y = a x1 + exp(a) x2

(P0) Identifikation: Zu gegebenen Werten (x1, x2, y) soll a ermittelt werden.

Dieses Problem läßt sich vergleichen mit der Zielsuche (P2) beim nichtlinearen Basismodell (S0010), die i.a. nur durch numerische Methoden (M2) lösbar ist. Dort würde es dann etwa in der Form

y = x a1 + exp(x) a2

erscheinen.