Effektivzinsberechnung

Ausgangspunkt ist das dynamisch-rekursives Basismodell S1000 mit den speziellen Problemen der Finanzmathematik.

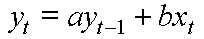
a    := q    = Wachstumsrate (=1+p, p = Zinssatz)
b    := r    = regelmäßige Zahlung
y[t] := K[t] = Kapital nach t Perioden
T    := n    = Laufzeit
y[0] := K[0] = 0
y[T] := K[n] = REW = Rentenendwert

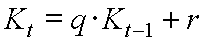
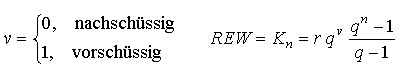
Bisher wurde nur die nachschüssige Zahlung beschrieben. Die vorschüssige Zahlung entspricht einer nachschüssige Zahlung einer einmal verzinsten Rate r'=rq. Mit Hilfe der zweiwertigen Variablen v lassen sich beide Fälle zusammen behandeln.

Die Auflösung nach q ist i.a. nicht durch Angabe einer geschlossenen Formel möglich. Das Problem der Effektivzinsberechnung besteht gerade darin, den Wert q so zu wählen, daß zu vorgegebenen Werten für die Rate r und die Laufzeit n ein ebenfalls vorgegebener Sollwert REW erzielt wird.

Das Problem der Effektivzinsberechnung läßt sich innerhalb der SPM-Systematik als Identifikationsproblem (P0) einordnen. Als zu identifizierenden Parameter kommen r und q in Frage.

Zur Effektivzinsberechnung kann man das Laufzeitverfahren verwenden.

Beispiel: Effektivzins

Ein Darlehen von 10 000 DM soll innerhalb von 6 Jahren zurückgezahlt werden.
Folgende Fälle sind zu untersuchen:                                            
                                                                               
(a)     am Anfang jedes Jahres (= vorschüssig) 2400 DM,                        
(b)     am Anfang jeden Monats (= vorschüssig) 200 DM,                         
(c)     am Ende jeden Monats (= nachschüssig) 200 DM.                          
                                                                               
Ermitteln Sie den Effektivzinssatz.