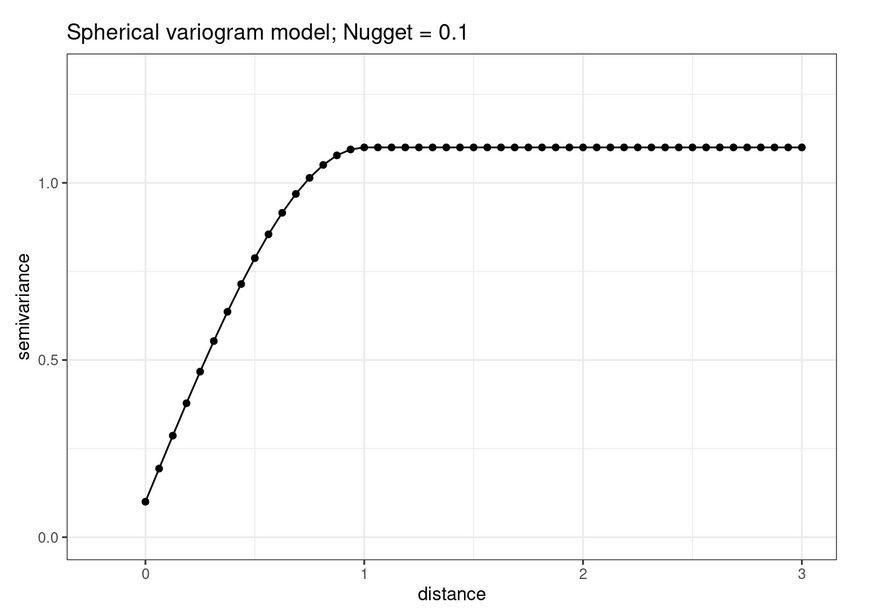
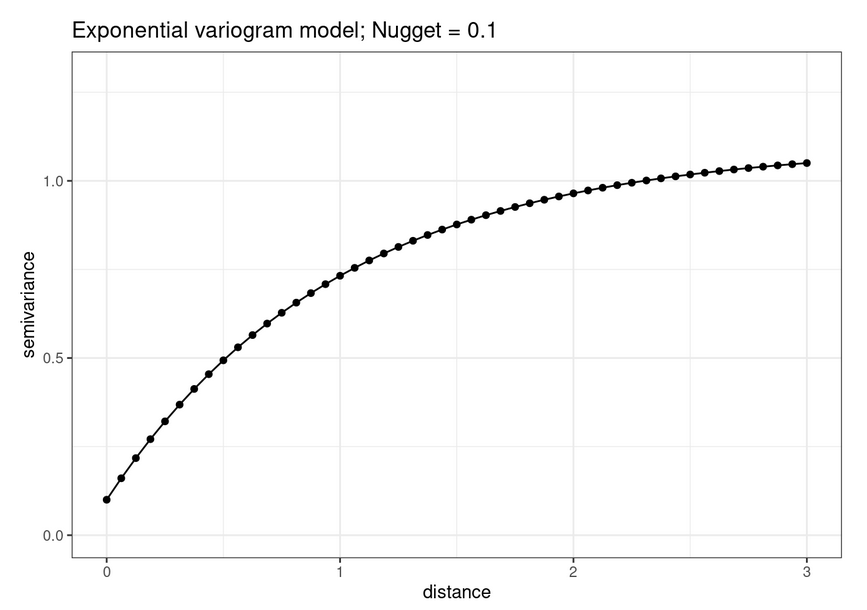
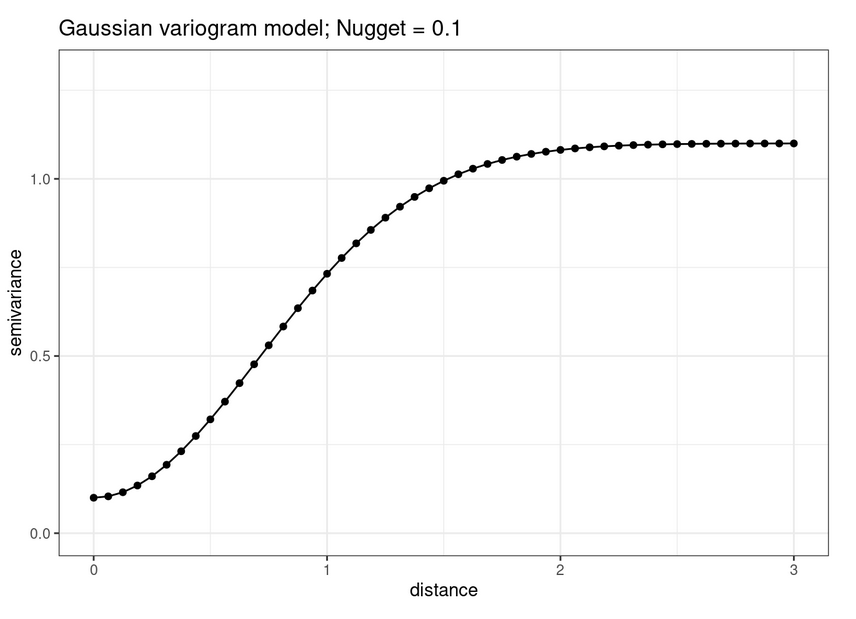
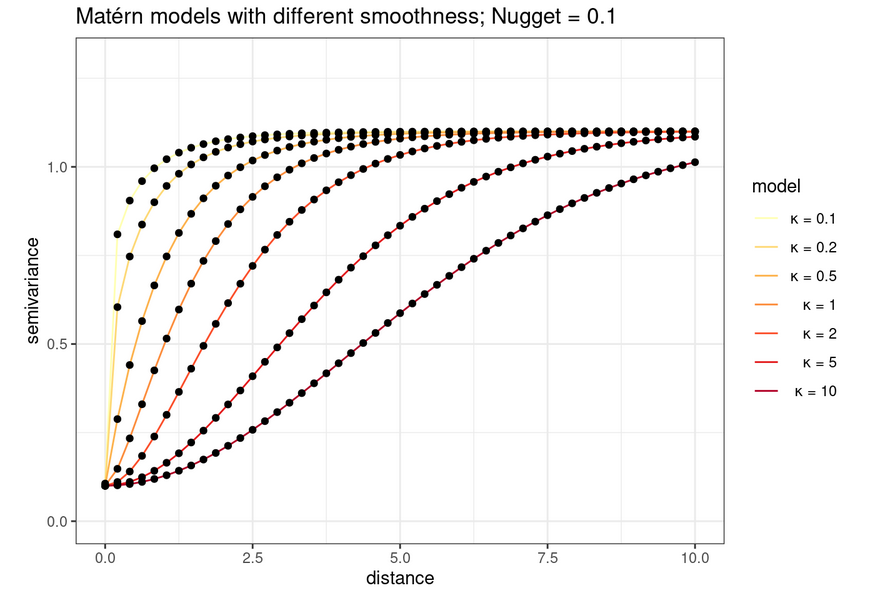
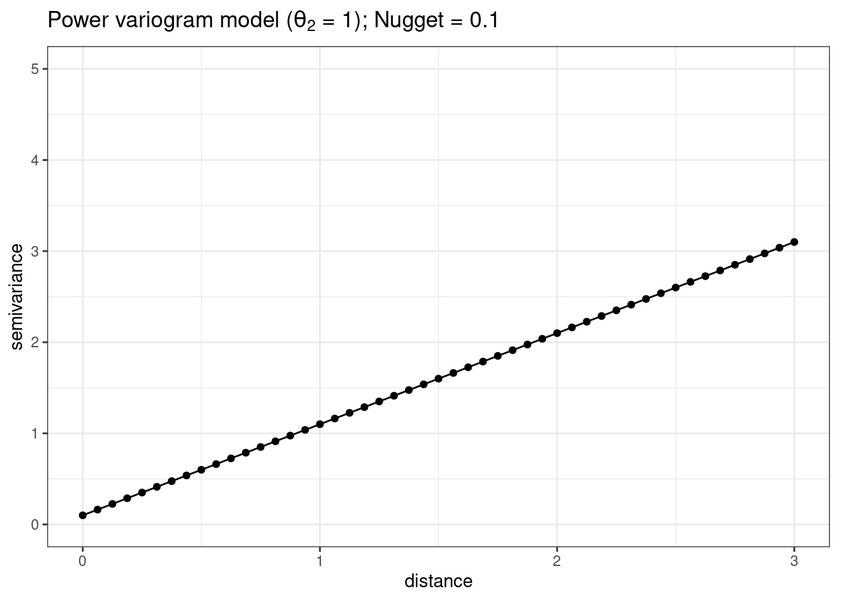
Once we calculate an sample variogram, it is standard practice to smooth the empirical semivariogram by fitting a parametric model to it.

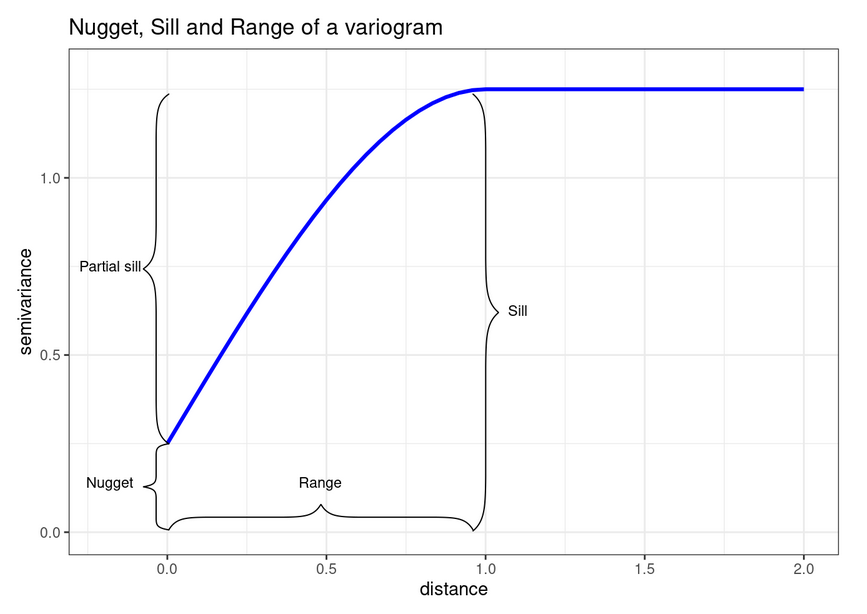
The nugget, the sill and the range parameters are often used to describe variograms:

• nugget: The random error process indicated by the height of the jump of the semivariogram at the discontinuity at the origin.
• sill: The limit of the variogram tending to infinity lag distances.
• range: The distance in which the difference of the variogram from the sill becomes negligible. In models with a fixed sill, it is the distance at which this is first reached; for models with an asymptotic sill, it is conventionally taken to be the distance when the semivariance first reaches 95% of the sill.

---

The following five parametric model are the most commonly used (Gelfand at al. 2010):

• Spherical

$$ \gamma(h, \theta) = \begin{cases} \theta_1 (\frac{3h}{2\theta_2}- \frac{h^3}{2\theta_2^3}) & \text{for } 0\le h \le \theta_2 \\ \theta_1 & \text{for } h > \theta_2 \end{cases}$$

• Exponential

$$\gamma(h, \theta)= \theta_1\{1- \exp(-h/\theta_2)\}$$

• Gaussian

$$\gamma(h, \theta)= \theta_1\{1- \exp(-h^2/\theta_2^2)\}$$

• Matérn

$$\gamma(h, \theta)= \theta_1\left( 1- \frac{(h/\theta_2)^\nu\kappa_\nu(h/\theta_2))}{2^{\nu-1}\Gamma(\nu)}\right)$$

where $\kappa_\nu(\cdot)$ is the modified Bessel function of the second kind of order $\nu$.

• Power

$$\gamma(h, \theta)= \theta_1h^{\theta_2}$$

---

Citation

The E-Learning project SOGA-Py was developed at the Department of Earth Sciences by Annette Rudolph, Joachim Krois and Kai Hartmann. You can reach us via mail by soga[at]zedat.fu-berlin.de.

You may use this project freely under the Creative Commons Attribution-ShareAlike 4.0 International License.

Please cite as follow: Rudolph, A., Krois, J., Hartmann, K. (2023): Statistics and Geodata Analysis using Python (SOGA-Py). Department of Earth Sciences, Freie Universitaet Berlin.