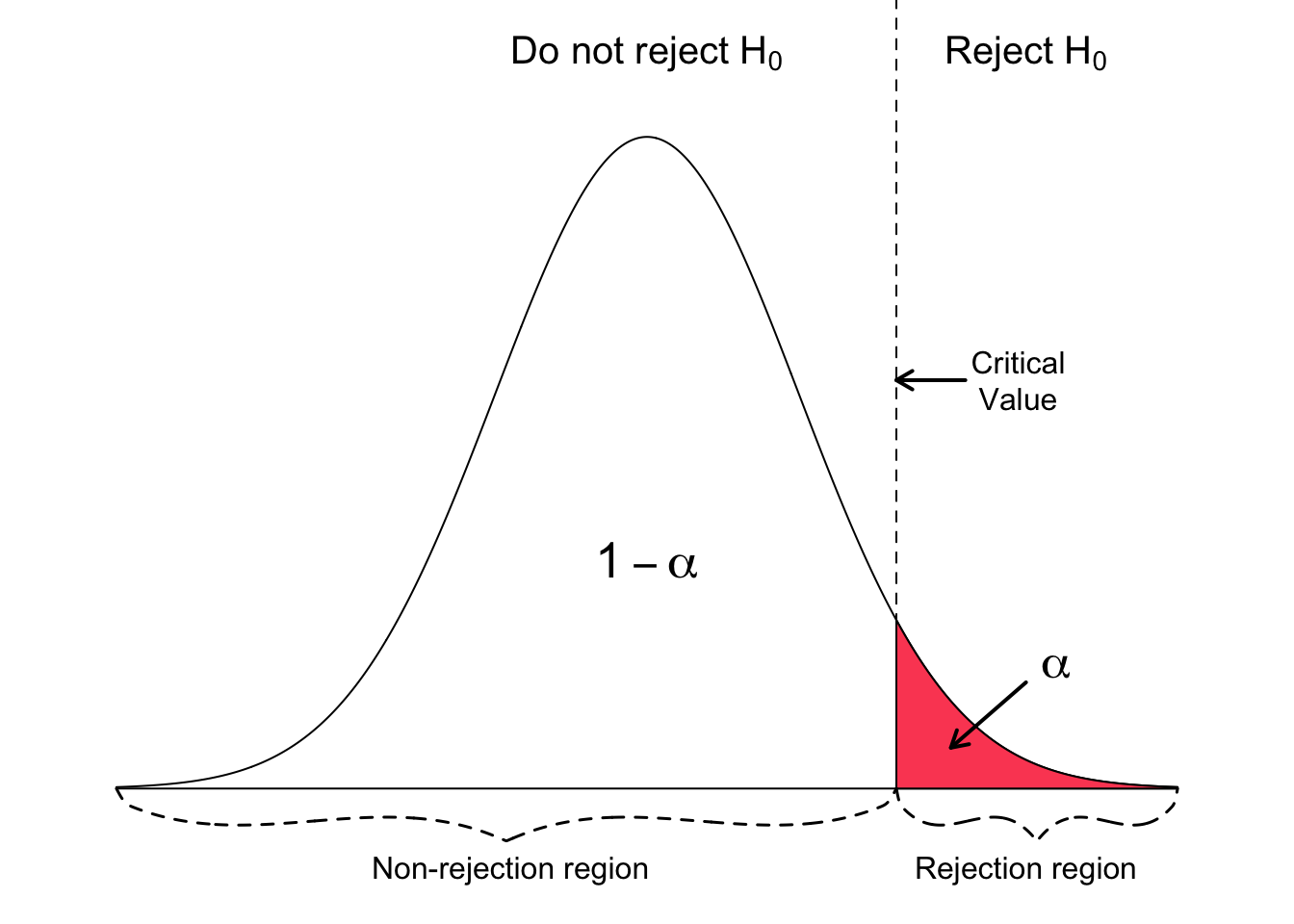
The critical value approach¶
By applying the critical value approach, it is determined whether or not the observed test statistic is more extreme than a defined critical value. Therefore, the observed test statistic (calculated based on sample data) is compared to the critical value (a kind of cutoff value). The null hypothesis is rejected if the test statistic is more extreme than the critical value. The null hypothesis is not rejected if the test statistic is not as extreme as the critical value. The critical value is computed based on the given significance level $\alpha$ and the type of probability distribution of the idealized model. The critical value divides the area under the probability distribution curve in rejection region(s) and non-rejection region.
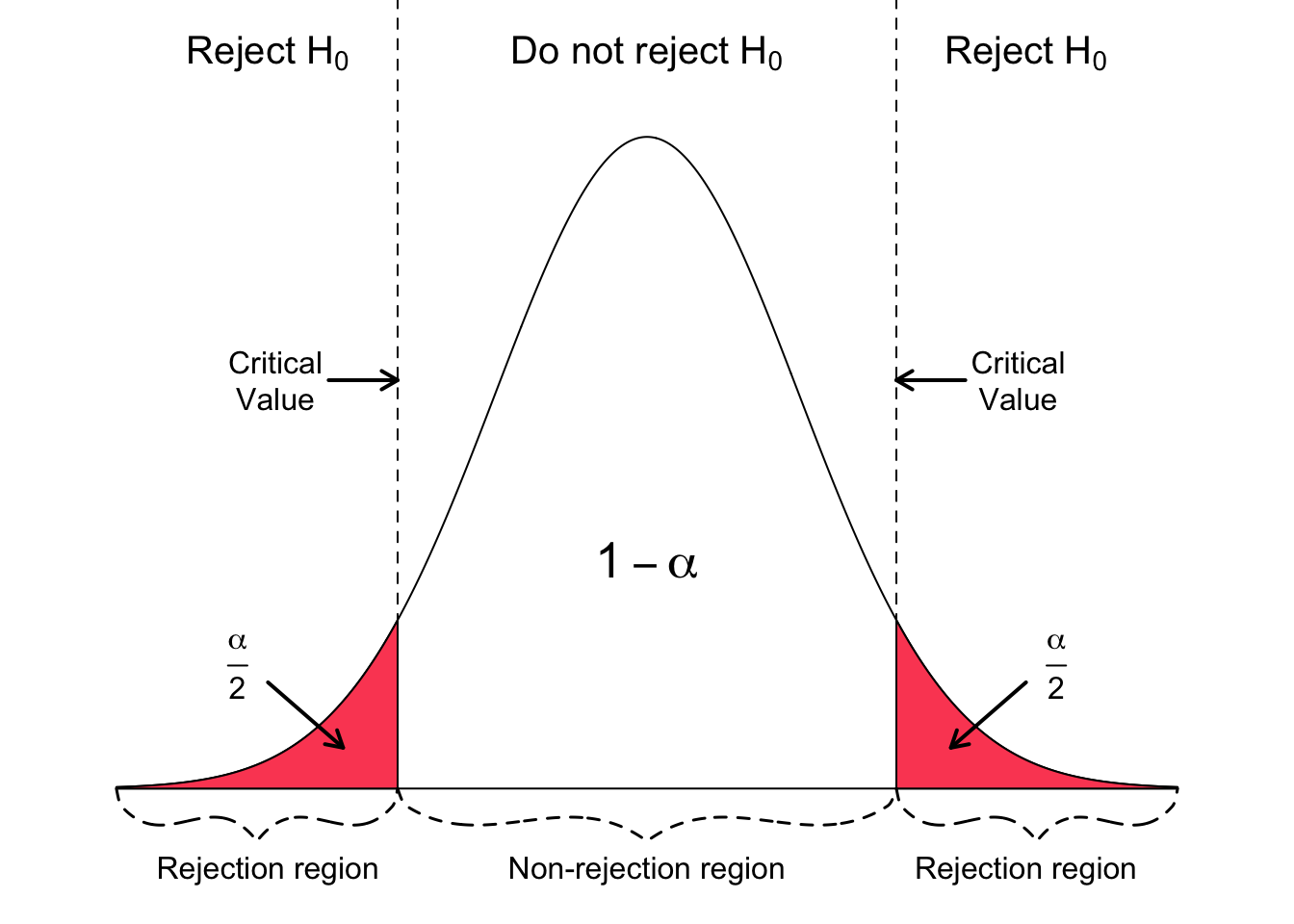
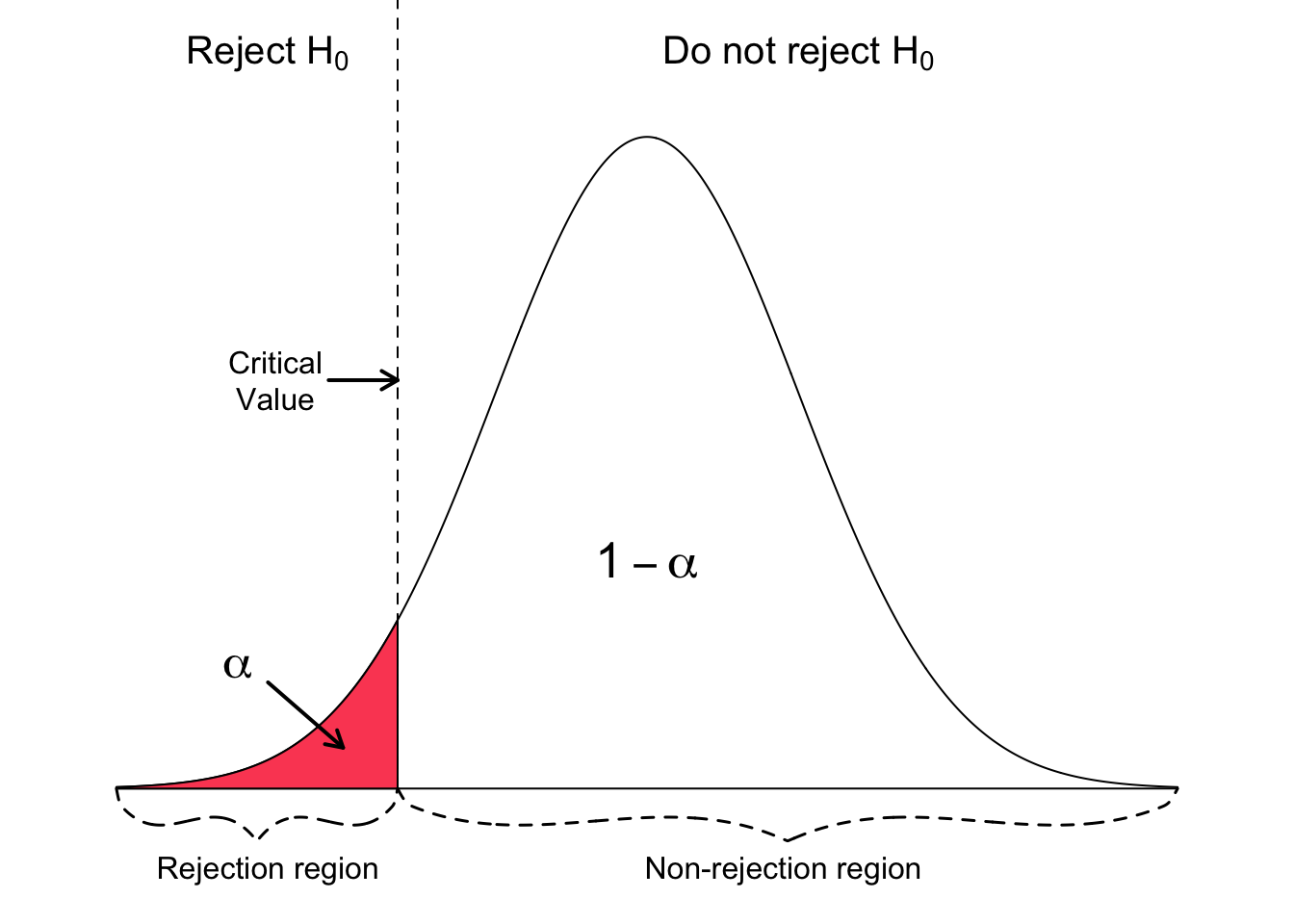
The following three figures show a right-tailed, left-tailed, and two-sided test. The idealized model in the figures, and thus $H_{0}$, is described by a bell-shaped normal distribution curve.
In a two-sided test, the null hypothesis is rejected if the test statistic is too small or too large. Thus, the rejection region for such a test consists of two parts: one on the left and one on the right.
The null hypothesis is rejected for a left-tailed test if the test statistic is too small. Thus, the rejection region for such a test consists of one part left from the centre.
The null hypothesis is rejected for a right-tailed test if the test statistic is too large. Thus, the rejection region for such a test consists of one part right from the centre.