Instead of assigning a single value to a population parameter, an interval estimation gives a probabilistic statement, relating the given interval to the probability that this interval actually contains the true (unknown) population parameter.

The level of confidence is chosen a priori and thus depends on the user's preferences. It is denoted by

$$100(1−\alpha)\%$$

Although any value of confidence level can be chosen, the most common values are 90 %, 95 % and 99 %. When expressed as a probability, the confidence level is called the confidence coefficient and is denoted by $(1−\alpha)$. Most common confidence coefficients are 0.90, 0.95 and 0.99, respectively.

A $100(1−\alpha)\%$ confidence interval is an interval estimate around a population parameter $\theta$ (here, the Greek letter $\theta$ (theta) is a placeholder for any population parameter of interest, such as the mean $\mu$ or the standard deviation $\sigma$, among others) that, under repeated random samples of size $N$, is expected to include $\theta$’s true value $100(1−\alpha)\%$ of the time (Lovric 2010).

---

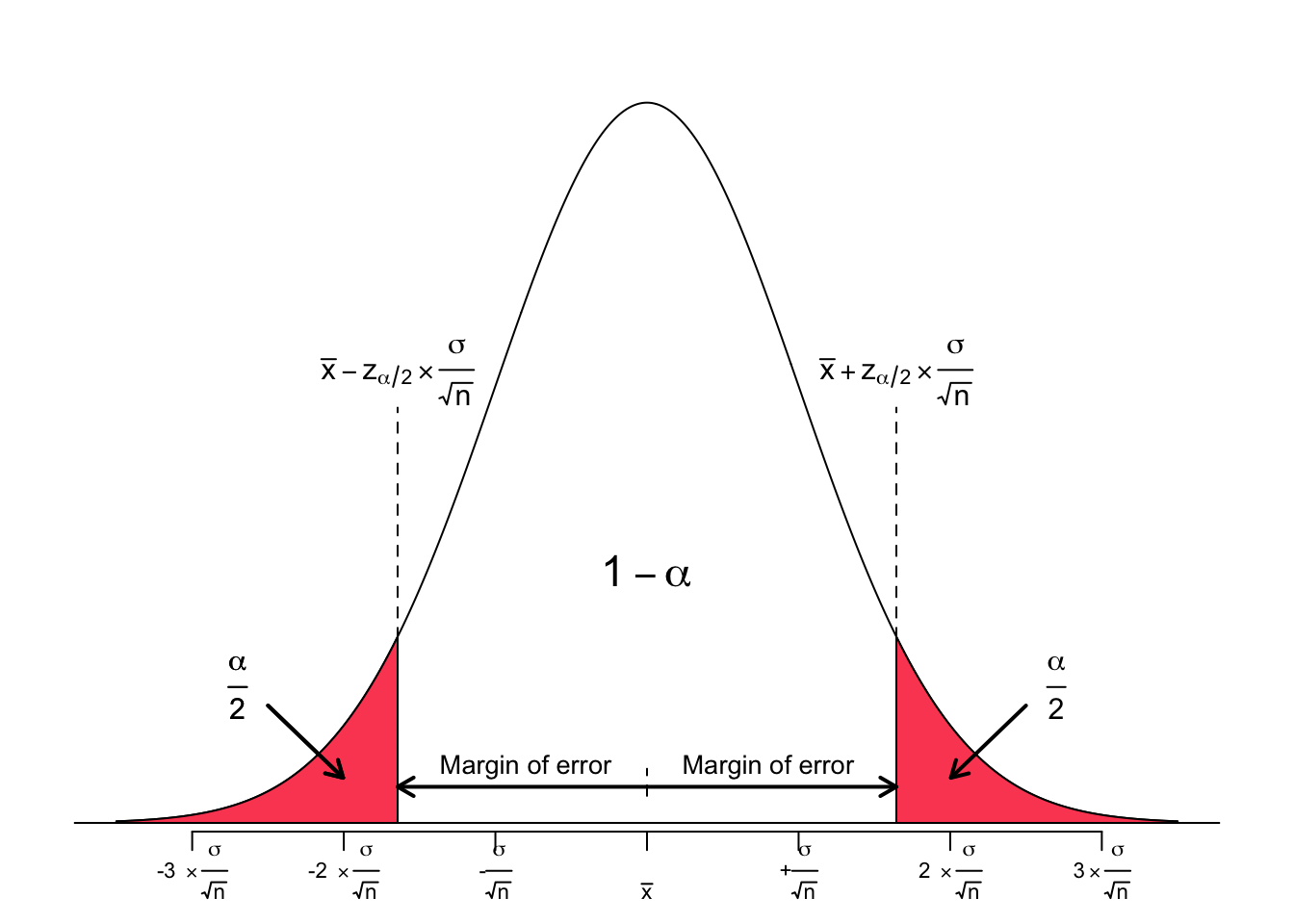
The actual number added to and subtracted from the point estimate is called the margin of error.

$$CI:Point\ estimate \pm Margin\ of\ error$$

The margin of error constitutes of two entities. First, the so called critical value and second, a measure of variability of the sampling distribution. The critical value is a numerical value that corresponds to the a priori set level of confidence. It is denoted as $z^{*}$. The relation to the level of confidence is made explicit by the subscript $z^{*}_{\alpha/2}$.

Note: The confidence interval has a lower and an upper limit. Consequently, $\alpha$ is divided by 2 as the area under the curve beyond those limits corresponds to $\frac {\alpha} {2} \times 2 = \alpha$.

The measure of variability is the standard error, denoted as $\frac {\sigma} {\sqrt {n}}$, if $\sigma$ is known. If $\sigma$ is not known, the sample standard error given by $\frac {s} {\sqrt {n}}$, where $s$ is the standard deviation of the sample, may be chosen instead.

Thus, the margin of error (ME) is expressed as:

$$ME = z^*_{\alpha /2} \times \frac {\sigma} {\sqrt {n}}$$

Let us look at a figure for better comprehension:

Accordingly, the full equation for the confidence interval is given by:

$$CI:Point\ estimate \pm z^{*}_{\alpha / 2} \times \frac {\sigma} {\sqrt {n}}$$

There are two ways to derive the corresponding value for $z^{*}_{\alpha / 2}$. One may look it up in a quantile table of the standard gaussian distribution. The other and state-of-the-art possibility is to utilise Python directly returning the corresponding $z$ value based on the chosen significance level. For this purpose the norm object and the .ppf(<probability>) method out of the scipy package is used.

Let us construct some confidence intervals for practice:

Note: Make sure that the scipy package is part of your mamba environment!

Confidence level of $90\ \%\ (\alpha=0.1)$

from scipy.stats import norm

lower_90 = norm.ppf(0.05)
upper_90 = norm.ppf(0.95)

print("The lower and upper limits of the interval that covers an area of 90% around the mean are given by z-scores of",
  round(lower_90, 2), "and", round(upper_90, 2), "respectively.")

The lower and upper limits of the interval that covers an area of 90% around the mean are given by z-scores of -1.64 and 1.64 respectively.

For a confidence level of 90 % ($\alpha=0.1$) the equation from above evaluates to:

$$CI_{90\%} : Point\ estimate \pm 1.64 \times \frac {\sigma} {\sqrt{n}}$$

Confidence level of $95\ \%\ (\alpha=0.05)$

lower_95 = norm.ppf(0.025)
upper_95 = norm.ppf(0.975)

print("The lower and upper limits of the interval that covers an area of 90% around the mean are given by z-scores of",
  round(lower_95, 2), "and", round(upper_95, 2), "respectively.")

The lower and upper limits of the interval that covers an area of 90% around the mean are given by z-scores of -1.96 and 1.96 respectively.

For a confidence level of 95 % ($\alpha=0.05$) the equation from above evaluates to:

$$CI_{95\%} : Point\ estimate \pm 1.96 \times \frac {\sigma} {\sqrt{n}}$$

Confidence level of $99\ \%\ (\alpha=0.01)$

lower_99 = norm.ppf(0.005)
upper_99 = norm.ppf(0.995)

print("The lower and upper limits of the interval that covers an area of 90% around the mean are given by z-scores of",
  round(lower_99, 2), "and", round(upper_99, 2), "respectively.")

The lower and upper limits of the interval that covers an area of 90% around the mean are given by z-scores of -2.58 and 2.58 respectively.

For a confidence level of 99 % ($\alpha=0.01$) the equation from above evaluates to:

$$CI_{99\%} : Point\ estimate \pm 2.58 \times \frac {\sigma} {\sqrt{n}}$$

---

Citation

The E-Learning project SOGA-Py was developed at the Department of Earth Sciences by Annette Rudolph, Joachim Krois and Kai Hartmann. You can reach us via mail by soga[at]zedat.fu-berlin.de.

You may use this project freely under the Creative Commons Attribution-ShareAlike 4.0 International License.

Please cite as follow: Rudolph, A., Krois, J., Hartmann, K. (2023): Statistics and Geodata Analysis using Python (SOGA-Py). Department of Earth Sciences, Freie Universitaet Berlin.