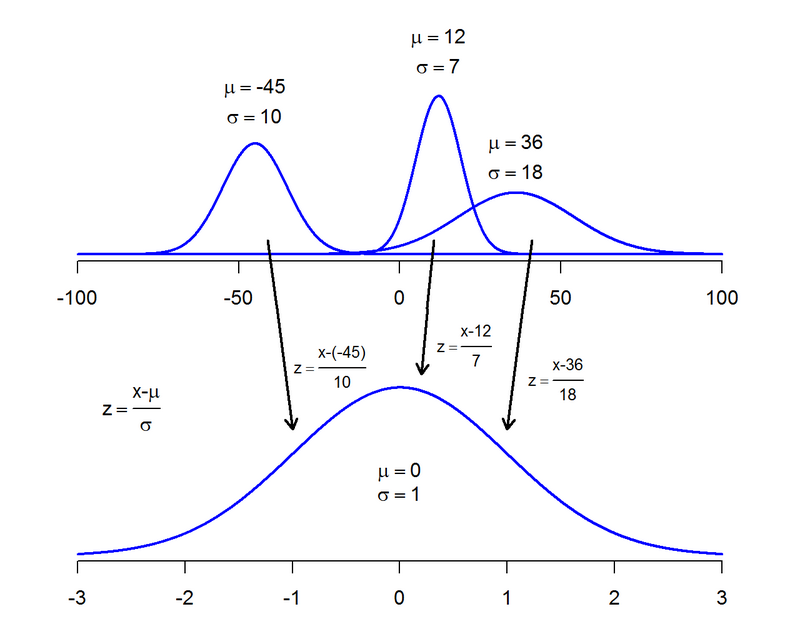
Before we can apply the concept of a standard normal distribution to a real data set we need to discuss the concept of standardization of a normal distribution. We know that a normal distribution is parametrized by two parameters, its mean $\mu \in \mathbb R$ and its standard deviation $\sigma \in \mathbb R>0$, $X \sim N(\mu,\sigma)$. The actual value of these parameters depends on the population and the metrics used to describe its features. In order to transform any particular $\mu$ and $\sigma$, related to a particular random variable $X$, to $\mu=0$ and $\sigma=1$, we have to convert the $x$-value to a $z$-value, by applying the equation below.
$$z = \frac{x-\mu}{\sigma}$$As a result we get a standard normal distribution for any particular normal distribution. This procedure is essential if you need to determine the $z$-scores or any particular probability related to a $z$-score $(P(z))$ by looking them up in a table. We will see later on, that R is such a powerful tool, which makes the step of standardization dispensable.

Citation
The E-Learning project SOGA-Py was developed at the Department of Earth Sciences by Annette Rudolph, Joachim Krois and Kai Hartmann. You can reach us via mail by soga[at]zedat.fu-berlin.de.

Please cite as follow: Rudolph, A., Krois, J., Hartmann, K. (2023): Statistics and Geodata Analysis using Python (SOGA-Py). Department of Earth Sciences, Freie Universitaet Berlin.