Global properties of dynamical systems can be studied by analyzing transfer operators such as the Perron-Frobenius or Koopman operator associated with the system. The aim is to approximate eigenfunctions of these operators from simulation or measurement data:
- Dimensionality reduction.
- Detection of metastable sets.
- Separation of time-scales.
- System identification.

Molecular dynamics
We are in particular interested in identifying so-called almost invariant or metastable sets – which in the molecular dynamics context correspond to conformations of molecules – and transitions between these sets. The goal is to understand important biological phenomena, e.g., protein folding or protein-ligand binding processes.
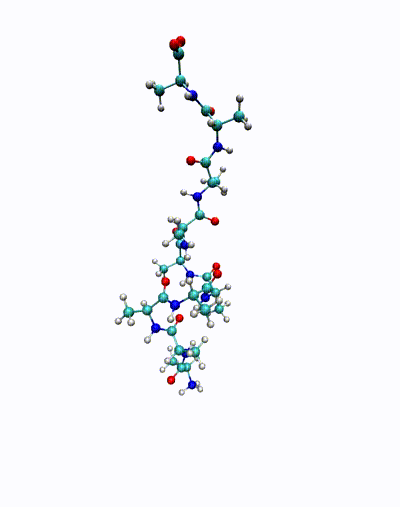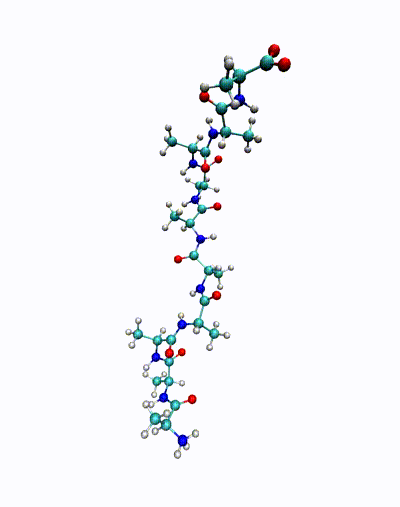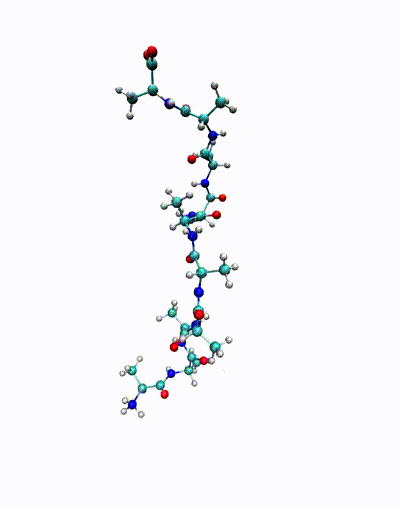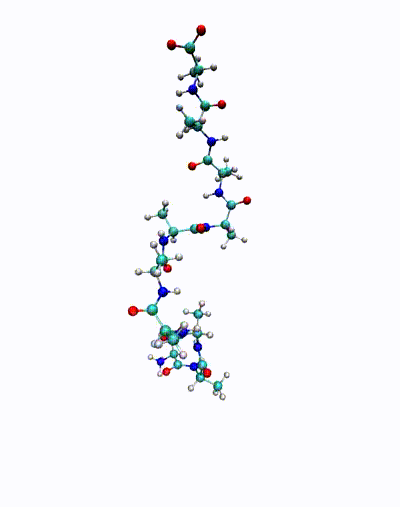

The animation shows a simulation of the deca-alanine molecule. Here, the slowest time-scale corresponds to the ?-helix formation.
Fluid dynamics
Similar approaches are also used for model reduction. Fluid dynamics problems, for instance, whose numerical solution is typically time-consuming, can be coarse-grained by projecting the system’s dynamics onto the dominant Koopman eigenfunctions or modes. In this way, it is possible to derive surrogate models that can then be used, for instance, for uncertainty quantification, sensitivity analysis, optimization, or control.
