Mediationsanalyse

Methoden der empirischen Kommunikations- und Medienforschung

Marko Bachl

Freie Universität Berlin

Evaluation

Fragen zur Hausaufgabe?

Mediationsanalyse

Agenda

  1. Einführung
  2. Beispielstudie
  3. Mediation mit mehreren Regressionsmodellen
  4. Mediation mit einem Strukturgleichungsmodell
  5. Fazit

Einführung

Wiederholung: Chain & Mediator

  • uV: unabhängige Variable, von der Effekt ausgeht

  • aV: abhängige Variable, die von uV beeinflusst wird

  • Mediator: Variable, die von uV beeinflusst wird und dann wiederum aV beeinflusst.

  • Kontrolle des Mediator nicht erlaubt, wenn wir gesamten kausalen Effekt von uV auf aV schätzen wollen.

  • Analyse mit Mediator manchmal gewünscht, wenn wir den Prozess uV → Mediator → aV untersuchen wollen (“indirekter Effekt”)

  • Typisches Problem: Kontrolle von Mediator unterschätzt den kausalen Effekt von uV und aV (“overcontrol/overadjustment bias”)

Interessanter kausaler Effekt

G uV uV aV aV uV->aV

Folgen bei unpassender Spezifikation

G Mediator Mediator aV aV Mediator->aV uV uV uV->Mediator uV->aV

Mediationsanalyse

  • Mediator: Variable, die von uV beeinflusst wird und dann wiederum aV beeinflusst

  • Die Mediationsanalyse interessiert sich für diesen kausalen Prozess. Sie will erklären, wie oder warum eine uV einen Effekt auf die aV hat.

  • Dazu wird der indirekten Effekt einer uV über den Mediator auf die aV geschätzt.

  • Eine Mediationsanalyse ist immer eine kausale Analyse. Das statistische Schätzen von Mediationsmodellen und indirekten Effekten geht immer davon aus, dass das kausale Modelle korrekt identifiziert ist.

  • Es gibt keine nicht kausale Mediation. Statistisch betrachtet sind Mediator- und Confounder-Variablen austauschbar (MacKinnon et al., 2000)

Fragen?

Beispielstudie

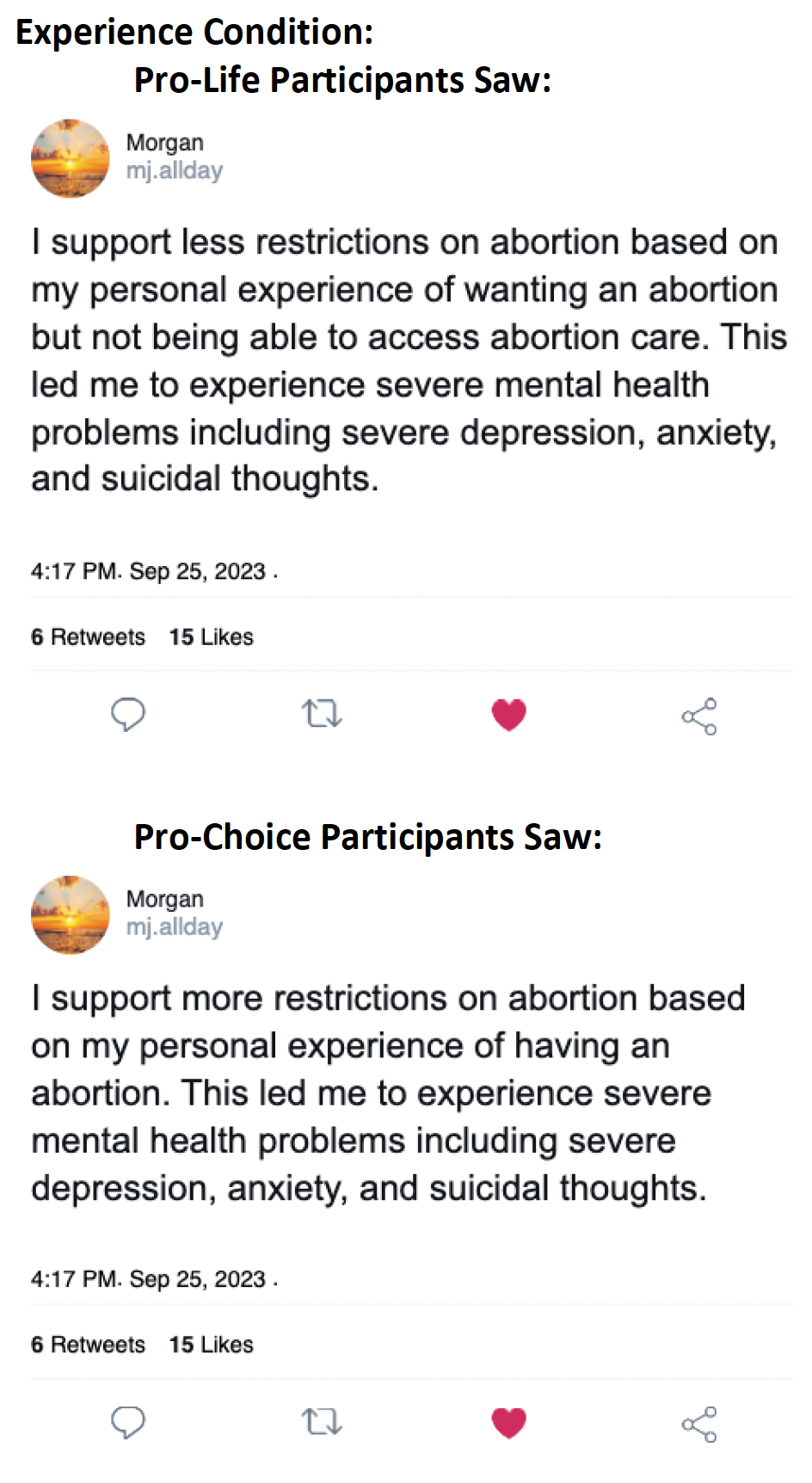
Daten der heutigen Sitzung

(Kubin et al., 2025)

Daten der heutigen Sitzung

(Kubin et al., 2025)

(Kubin et al., 2025)

Daten der heutigen Sitzung

  • Condition: Fact (0), Experience (1)
  • Harm: 3 Items, z.B. “causes harm”
  • Lie: 3 Items, z.B. “is a lie”
  • Censor: 4 Items, z.B. “censor her”
  • Behave: 1 Item, “willing to report to Twitter”
  • Alle Range 1-7
Condition Harm Lie Censor Behave
Fact 4.67 5.00 1.00 1
Fact 6.33 5.67 1.75 1
Fact 2.67 5.33 2.75 3
Experience 2.00 2.00 1.00 1
Experience 3.00 3.00 2.00 1
Experience 4.67 5.00 4.00 4

Stichprobe

Descriptive Statistics
Variable Fact (n=198) Experience (n=199) Total (n=397)
Mean Age (SD) 42.66 (13.73) 43.75 (13.46) 43.20 (13.59)
Gender [female], % 48.5 47.0 47.7
Mean Harm (SD) 4.84 (1.60) 4.02 (1.73) 4.43 (1.71)
Mean Lie (SD) 4.99 (1.40) 3.44 (1.47) 4.22 (1.63)
Mean Censor (SD) 2.98 (1.72) 2.27 (1.36) 2.62 (1.59)
Mean Behave (SD) 3.22 (1.94) 2.19 (1.45) 2.70 (1.79)

Gesamtes Modell

(Kubin et al., 2025)

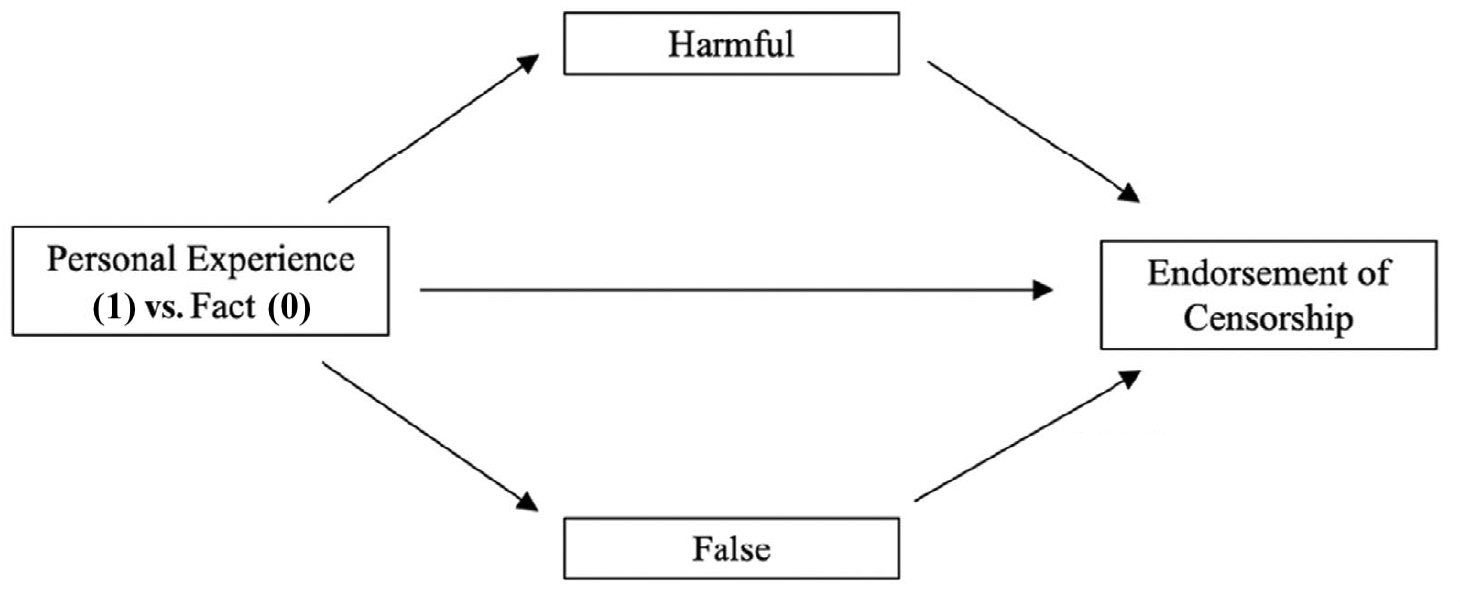
Vereinfachtes Modell als erstes Beispiel

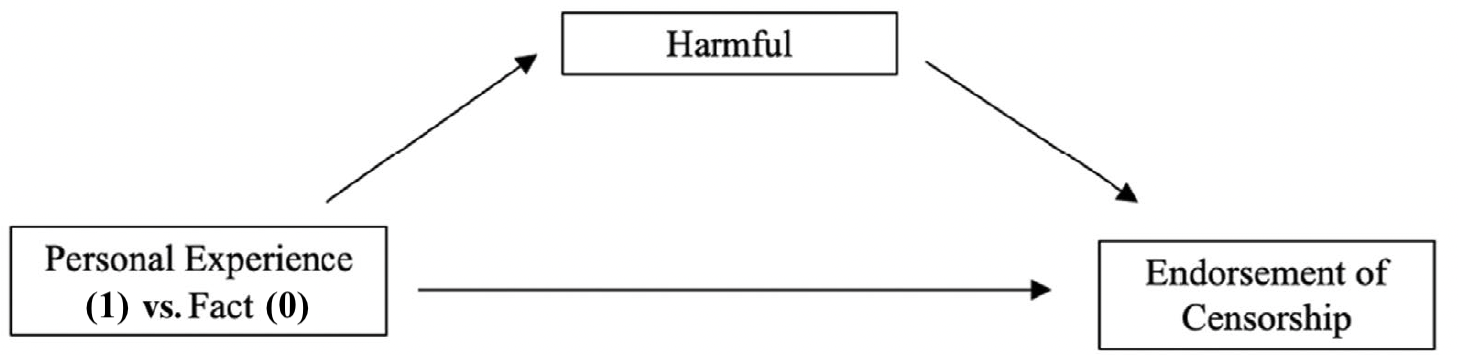
Fragen?

Mediation mit mehreren Regressionsmodellen

Drei Regressionsmodelle: I

lm(Censor ~ Condition, data = d)

Effekt des Treatments auf Censorship

Parameter Coefficient 95% CI t(395) p Fit
(Intercept) 2.98 (2.76, 3.19) 26.99 < .001
Condition (Experience) -0.71 (-1.02, -0.40) -4.56 < .001
R2 (adj.) 0.05

Drei Regressionsmodelle: II

lm(Harm ~ Condition, data = d)

Effekt des Treatments auf Harmful

Parameter Coefficient 95% CI t(395) p Fit
(Intercept) 4.84 (4.60, 5.07) 40.85 < .001
Condition (Experience) -0.81 (-1.14, -0.49) -4.87 < .001
R2 (adj.) 0.05

Drei Regressionsmodelle: III

lm(Censor ~ Condition + Harm, data = d)

Effekte des Treatments und des Mediators auf Censorship

Parameter Coefficient 95% CI t(394) p Fit
(Intercept) 1.47 (1.00, 1.94) 6.17 < .001
Condition (Experience) -0.46 (-0.75, -0.16) -3.02 0.003
Harm 0.31 (0.23, 0.40) 7.06 < .001
R2 (adj.) 0.15

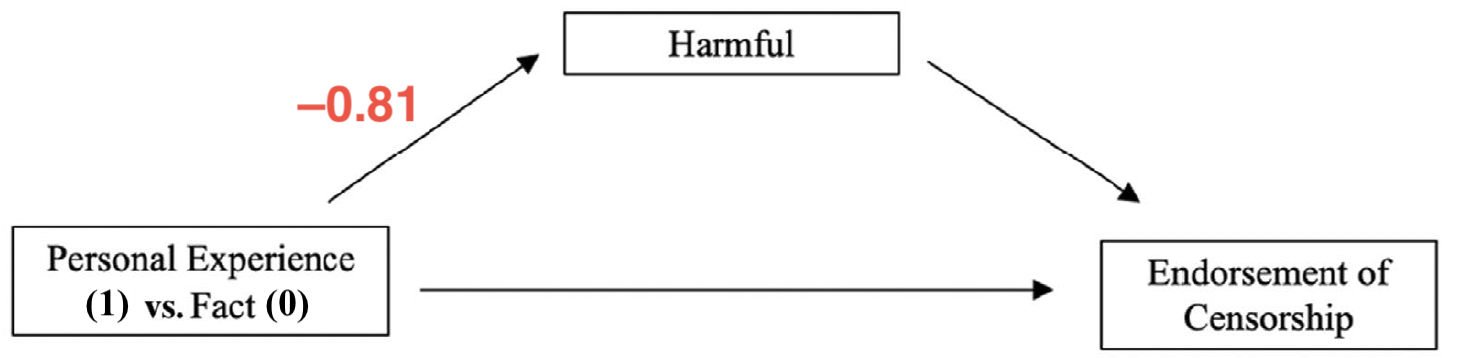
Indirekte, direkte und totale Effekte

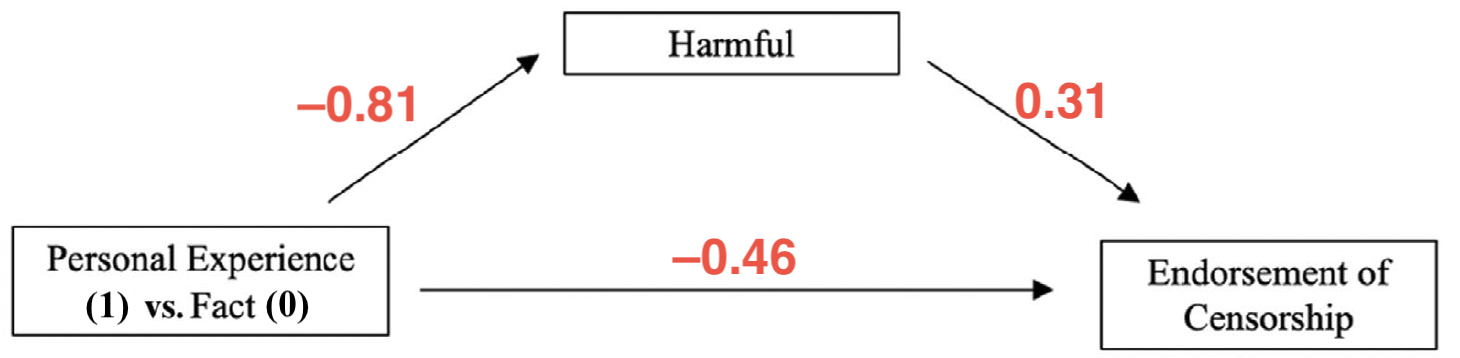
  • Totaler Effekt des Treatments auf Censorship: \(c = -0.71\)
  • Effekt des Treatments auf Harmful: \(a = -0.81\)
  • Effekt von Harmful auf Censorship bei Kontrolle des Treatments: \(b = 0.31\)
  • Direkter Effekt des Treatments bei Kontrolle von Harmful: \(c' = -0.46\)
  • Indirekter Effekt des Treatments über Harmful: \(a \times b = -0.25\)
  • Totaler Effekt = Indirekter Effekt + Direkter Effekt: \(c = ab + c' = -0.25 + -0.46 = -0.71\)

Fragen?

Gesamtes Modell

(Kubin et al., 2025)

Vier Regressionsmodelle: I

lm(Censor ~ Condition, data = d)

Effekt des Treatments auf Censorship

Parameter Coefficient 95% CI t(395) p Fit
(Intercept) 2.98 (2.76, 3.19) 26.99 < .001
Condition (Experience) -0.71 (-1.02, -0.40) -4.56 < .001
R2 (adj.) 0.05

Vier Regressionsmodelle: II

lm(Harm ~ Condition, data = d)

Effekt des Treatments auf Harmful

Parameter Coefficient 95% CI t(395) p Fit
(Intercept) 4.84 (4.60, 5.07) 40.85 < .001
Condition (Experience) -0.81 (-1.14, -0.49) -4.87 < .001
R2 (adj.) 0.05

Vier Regressionsmodelle: III

lm(Lie ~ Condition, data = d)

Effekt des Treatments auf False

Parameter Coefficient 95% CI t(395) p Fit
(Intercept) 4.99 (4.79, 5.19) 48.86 < .001
Condition (Experience) -1.55 (-1.83, -1.27) -10.75 < .001
R2 (adj.) 0.22

Vier Regressionsmodelle: IV

lm(Censor ~ Condition + Harm + Lie, data = d)

Effekte des Treatments und der Mediatoren auf Censorship

Parameter Coefficient 95% CI t(393) p Fit
(Intercept) 0.87 (0.31, 1.44) 3.05 0.002
Condition (Experience) -0.20 (-0.53, 0.12) -1.23 0.218
Harm 0.21 (0.11, 0.31) 4.11 < .001
Lie 0.22 (0.10, 0.33) 3.61 < .001
R2 (adj.) 0.18

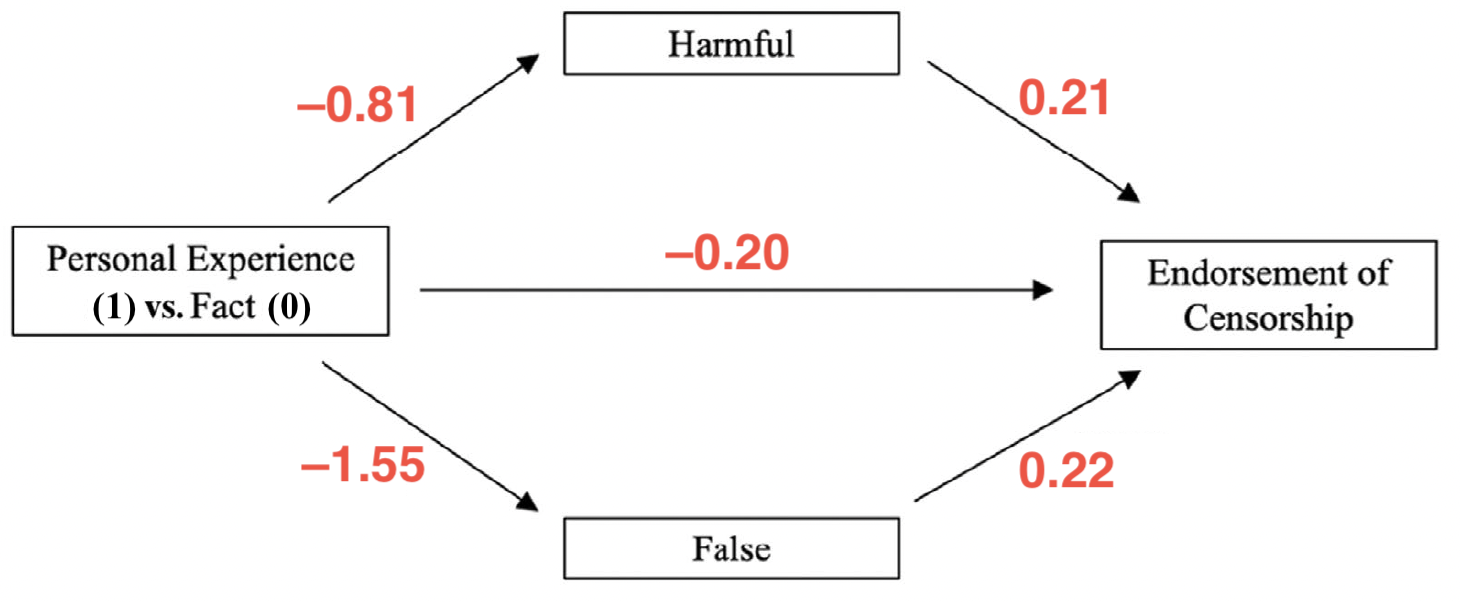
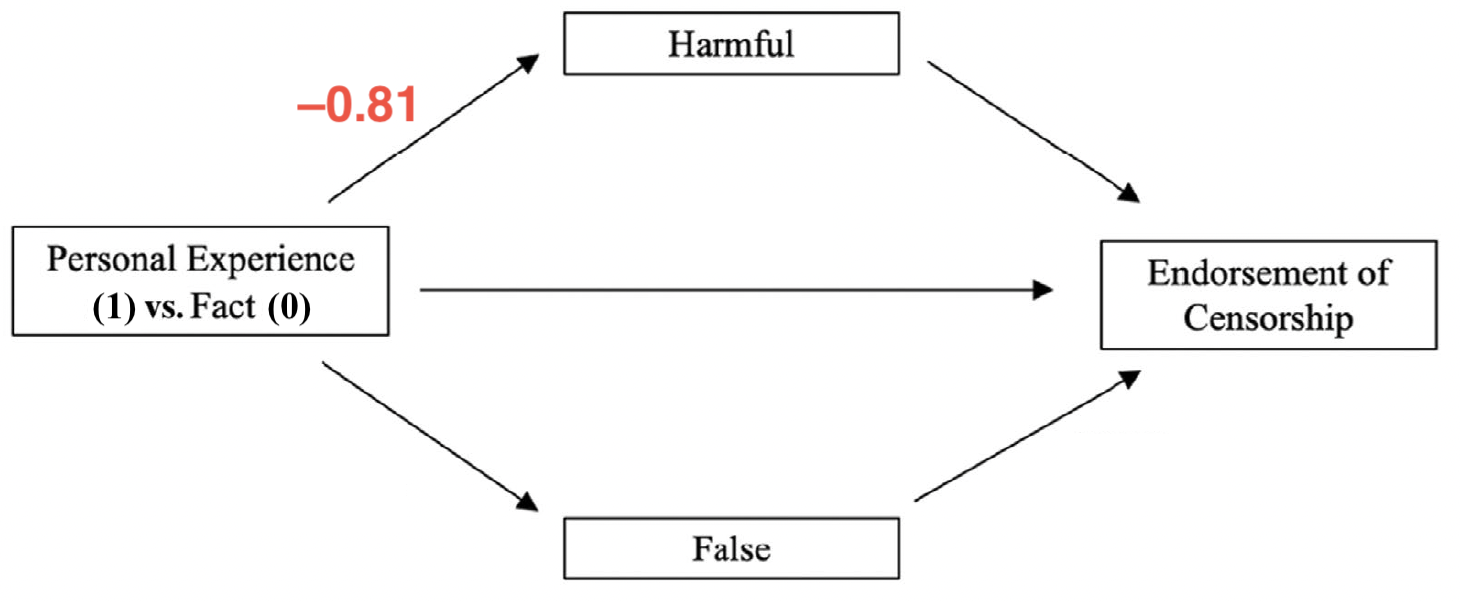
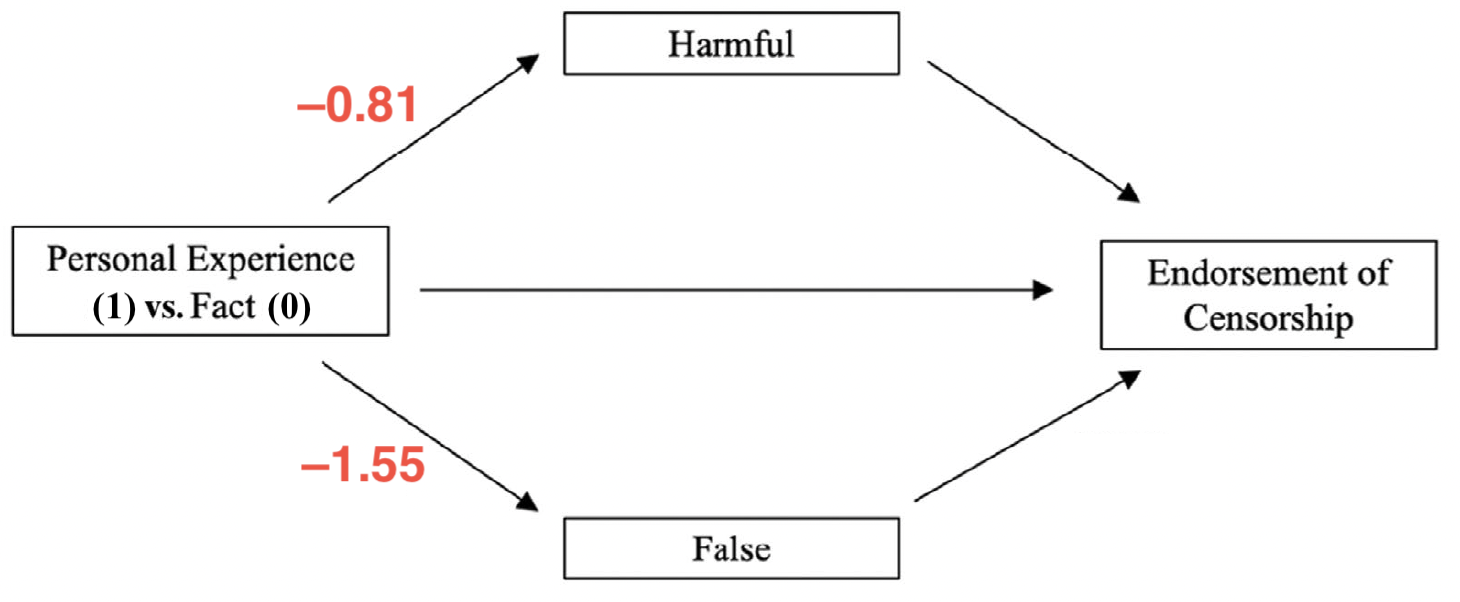
Indirekte, direkte und totale Effekte

  • Totaler Effekt: \(c = -0.71\); direkter Effekt: \(c' = -0.20\)
  • Indirekter Effekt über Harmful: \(a_1 \times b_1 = -0.81 \times 0.21 = -0.17\)
  • Indirekter Effekt über False: \(a_2 \times b_2 = -1.55 \times 0.22 = -0.34\)

Indirekte, direkte und totale Effekte

  • Der negative Effekt der Begründung mit einer persönlichen Erfahrung im Vergleich zur Begründung mit wissenschaftlichen Fakten auf die Zustimmung zu einer Zensur der Aussage wird durch die Einschätzung der Gefährlichkeit und der Falschheit vermittelt. Die Schilderung einer persönlichen Erfahrung wird als weniger gefährlich und weniger falsch eingeschätzt, was wiederum zu einer verringerten Zustimmung zur Zensur der Aussage führt.

  • Aber sind diese indirekten Effekte statistisch signifikant?

Fragen?

Mediation mit einem Strukturgleichungsmodell

Schätzen und Inferenzstatistik

Schätzen

  • Option 1: Mehrere Regressionsmodelle und spezielle Testverfahren
  • Option 2: Ein Strukturgleichungsmodell

Inferenzstatistik

  • In 2010er Jahren sehr aktives Forschungsfeld; wir steigen in diesem Rahmen nicht tiefer in die Debatten ein. Für Interessierte: Hayes & Scharkow (2013)
  • Heute stärkerer Fokus auf Annahmen für Identifikation kausaler Effekte

Strukturgleichungsmodelle

  • Englisch Structural Equation Models (daher Abkürzung SEM gebräuchlich)
  • Schätzung von mehreren Gleichungen in einem Modell
  • Schätzung meist mit Maximum-Likelihood-Verfahren und deren Varianten
  • Wesentliche Vorteile gegenüber mehreren Regressionsmodellen:
    • Einfach zu spezifizieren und trotzdem sehr flexibel
    • Statistische Tests für selbst definierte Paramenter, z.B. indirekte Effekte
    • Messmodelle: Latente Variablen aus Indikatoren schätzen

Strukturgleichungsmodelle

  • Hier nur konzeptionelle und praktische Einführung zur Mediationsanalyse
  • Einstieg in die Vertiefung (nicht klausurrelevant):

Ein Pfadmodell

modell <- "
# Modelle
# Mediator 1: Harm
Harm ~ a1 * Condition
# Mediator 2: False
Lie ~ a2 * Condition
# aV: Endorsement of Censorship
Censor ~ c_ * Condition + b1 * Harm + b2 * Lie
# Kovarianz zwischen Mediatoren
Harm ~~ Lie

# Effekte
# Indirekte Effekte
indirect_harm := a1 * b1
indirect_lie := a2 * b2

# Direkter Effekt
direct := c_

# Totaler Effekt
total := direct + indirect_harm + indirect_lie
"

Mediation im Pfadmodell

Nicht standardisierte Koeffizienzen der einzelnen Pfade

Parameter Coefficient CI z p
Harm ~ Condition -0.81 (-1.14, -0.49) -4.88 < .001
Lie ~ Condition -1.55 (-1.83, -1.27) -10.77 < .001
Censor ~ Condition -0.20 (-0.52, 0.12) -1.24 0.215
Censor ~ Harm 0.21 (0.11, 0.31) 4.13 < .001
Censor ~ Lie 0.22 (0.10, 0.33) 3.62 < .001

Mediation im Pfadmodell

Nicht standardisierte Koeffizienzen der zusammengesetzen Effekte

Parameter Coefficient CI z p
indirect_harm := a1*b1 -0.17 (-0.28, -0.07) -3.16 0.002
indirect_lie := a2*b2 -0.33 (-0.53, -0.14) -3.44 < .001
direct := c_ -0.20 (-0.52, 0.12) -1.24 0.215
total := direct+indirect_harm+indirect_lie -0.71 (-1.02, -0.41) -4.57 < .001


  • Der negative Effekt der Begründung mit einer persönlichen Erfahrung im Vergleich zur Begründung mit wissenschaftlichen Fakten auf die Zustimmung zu einer Zensur der Aussage wird durch die Einschätzung der Gefährlichkeit und der Falschheit vermittelt. Die Schilderung einer persönlichen Erfahrung wird als weniger gefährlich und weniger falsch eingeschätzt, was wiederum zu einer verringerten Zustimmung zur Zensur der Aussage führt.

  • Die indirekten Effekte vermittelt über die Einschätzung der Gefährlichkeit (\(a_1b_1 = -0.17\), 95%-KI \([-0.28, -0.07]\), \(z = 3.16\), \(p = .002\)) und der Falschheit (\(a_2b_2 = -0.33\), 95%-KI \([-0.53, -0.14]\), \(z = 3.44\), \(p < .001\)) sind statistisch signifikant.

Kausale Identifikation des Modells?

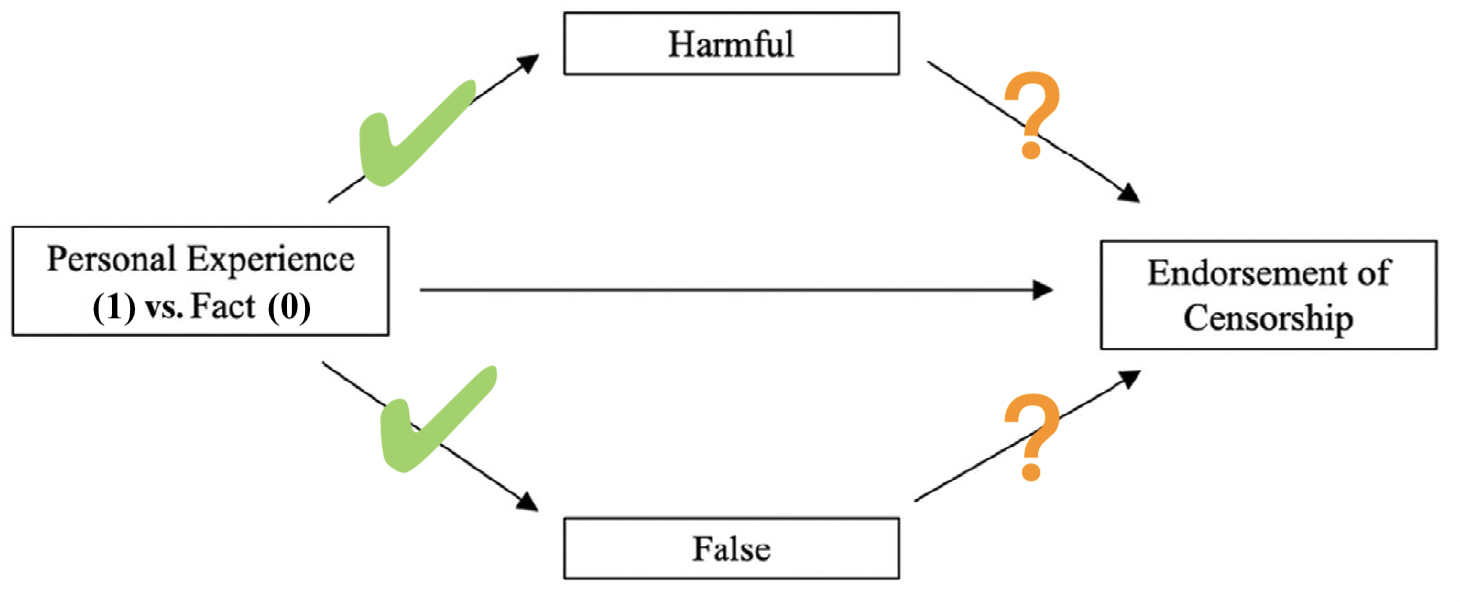
  • Randomisierte Zuteilung des Treatments: Identifikation durch Design
  • Gemessene Mediatoren: Identifikation durch theoretische Annahme
    • Da keine Kontrollvariablen im Modell sind, gilt die starke Annahme, dass es keine Confounder zwischen den Mediatoren und der aV gibt.

Fragen?

Fazit

  • Mediationsanalyse sieht leicht aus, ist aber schwer.

  • Mediationsmodelle sind in der Regel sehr leicht zu spezifizieren und lassen sich auf den ersten Blick intuitiv interpretieren. Allerdings sind sehr starke theoretische Annahmen nötig, um die kausalen Effekte zu identifizieren.

    • Das gilt auch dann, wenn das Treatment in einem Experimentaldesign randomisiert wird.
    • Mediationsanalysen auf Basis von reinen Querschnittsdesigns sollten grundsätzlich ignoriert werden.

  • Die statistisch geschätzten Effekte basieren auf der Annahme, dass das zugrunde liegende kausale Modell korrekt ist. Das statistische Modell kann diese Annahme nicht prüfen.

  • “Yes, but what’s the mechanism? (don’t expect an easy answer)” — Bullock et al. (2010)

  • “That’s a lot to process! Pitfalls of popular path models” — Rohrer et al. (2022)

Fragen?

Hausaufgabe

  1. Vollziehen Sie die Analysen nach, deren Ausgaben wir in der Vorlesung besprochen haben.
  2. Modifizieren Sie die Mediationsanalysen aus der Vorlesung.

Nächste Einheit

Messmodelle in Strukturgleichungsmodellen

Danke

Marko Bachl

Literatur

Arzheimer, K. (2016). Strukturgleichungsmodelle: Eine anwendungsorientierte Einführung. Springer Fachmedien. https://doi.org/10.1007/978-3-658-09609-0
Bullock, J. G., Green, D. P., & Ha, S. E. (2010). Yes, but what’s the mechanism? (don’t expect an easy answer). Journal of Personality and Social Psychology, 98(4), 550–558. https://doi.org/bw5pxx
Hayes, A. F., & Scharkow, M. (2013). The relative trustworthiness of inferential tests of the indirect effect in statistical mediation analysis: Does method really matter? Psychological Science, 24(10), 1918–1927. https://doi.org/bbhr
Keele, L., Stevenson, R. T., & Elwert, F. (2020). The causal interpretation of estimated associations in regression models. Political Science Research and Methods, 8(1), 1–13. https://doi.org/gf5sjg
Kubin, E., Sikorski, C. von, & Gray, K. (2025). Political censorship feels acceptable when ideas seem harmful and false. Political Psychology, 46(2), 279–299. https://doi.org/g9fgdz
MacKinnon, D. P., Krull, J. L., & Lockwood, C. M. (2000). Equivalence of the mediation, confounding and suppression effect. Prevention Science, 1(4), 173–181. https://doi.org/cmd8b5
Rohrer, J. M. (2018). Thinking clearly about correlations and causation: Graphical causal models for observational data. Advances in Methods and Practices in Psychological Science, 1(1), 27–42. https://doi.org/10.1177/2515245917745629
Rohrer, J. M., Hünermund, P., Arslan, R. C., & Elson, M. (2022). That’s a lot to process! Pitfalls of popular path models. Advances in Methods and Practices in Psychological Science, 5(2), 25152459221095827. https://doi.org/gqw5jr