Sei L dfa-Sprache, das heißt, es gibt einen dfa M, der L erkennt.

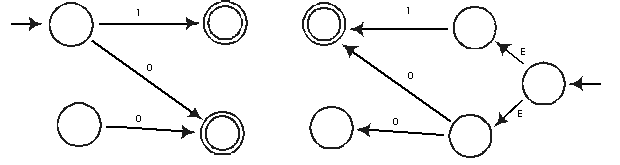
Konstruktion eines dfa M^R für L^R:

• Drehe alle Pfeile um.
• Der alte Startzustand wird akzeptierend und ist nicht mehr Startzustand.
• Die alten akzeptierenden Zustände sind nicht mehr akzeptierend.
• Ein neuer Startzustand wird eingefügt und mit Epsilon-Übergängen zu den alten akzeptierenden Zuständen verbunden.

Der nun entstandene Automat ist ein nfa, für den es nach Vorlesung einen äquivalenten dfa gibt, der nun L^R erkennt.

M^R erkennt alle umgedrehten Worte aus L, da für jedes Wort aus L der Pfad zurückverfolgt wird und es einen umgedrehten Pfad in M^R gibt.

M^R erkennt keine anderen Worte, denn für jedes Wort aus L(M^R) gibt es in M einen 'Vorwärtspfad'.

Sei L dfa-Sprache, dann ist L auch reguläre Sprache, und es gibt einen regulären Ausdruck A für L.

Wir konstruieren einen regulären Ausdrucks A^R (der L^R beschreibt), indem wir A von hinten nach vorn lesen. Der Stern wird aber jeweils nicht vor sein Argument, sondern dahinter geschrieben. [Bsp.: (01v1)*v1 wird zu 1v(1v10)*] A^R beschreibt eine dfa-Sprache, da die regulären den dfa-Sprachen entsprechen.

Seien A,B reguläre Ausdrücke.

Ind.anf.: n=0

Wenn A kein Verknüpfungssymbol enthält, besteht der reg. Ausdruck nur aus einem Symbol a oder Epsilon. Dieses von hinten gelesen wird durch A^R beschrieben.

Ind.vor.:

A^R und B^R stellen die 'Rückwärtsworte' der regulären Ausdrücke A, B dar.

Ind.schritt.: n->n+1

AB wird zu und B^RA^R, da beim Rückwärtslesen von AB zuerst B^R und dann A^R gelesen wird.

AvB wird zu und B^RvA^R, da das das gleiche ist wie A^RvB^R.

A* wird zu A^R*, da A zu A^R wird, und beim *-Operator die Reihenfolge der Argumente beliebig ist.

Die Idee ist, den Automaten für L dazu zu nutzen, das Präfix festzustellen, um danach ebenfalls mit L das Wort daraufhin zu untersuchen, ob es noch akzeptiert werden kann.

Zunächst bauen wir für den gegebenen dfa für L einen, der L\{Epsilon} akzeptiert, denn Epsilon soll nicht als (echtes) Teilwort gelten. Dazu verdoppelt man den (angenommen) akzeptierenden Startzustand, das Double wird akzeptierend, der alte ist es nicht mehr und alle Pfeile, die auf den alten zeigten (der ist weiterhin Startzustand !) werden auf das Double umgelenkt. Das Double zeigt auf die gleichen Zustände wie das Original.

Sei dieser neue Automat A=(Q,Sigma,d,s,F). s nicht in F.

Wir bauen 1 Kopie A' von A. Die Ausgänge der akzeptierenden Zustände im Original A werden auf die Kopie A' umgelenkt.

Die akzeptierenden Zustände vom ganzen sind jene von A'.