Das helle Muster im skalierten Bild entsteht durch den durchscheinenden Hintergrund an Stellen, wo Pixeln des Bildrasters kein Bild eines Urbildpixels zugeordnet wurde.
Um die Koordinaten des Originals in solche eines Bildes oder Modells umrechnen zu können,
ist eine Abbildungsvorschrift erforderlich, die das gewünschte Resultat liefert. Dazu bedarf es
eines mathematischen Modells, welches den geometrischen Zusammenhang (z.B. Projektion)
zwischen Urbild und Bild definiert.
Der nächste Schritt ist oft eine Vergrößerung oder Verkleinerung. Dabei ist die Frage zu beantworten, wie hinzukommende Pixel aufgefüllt werden. Auch sollen relative Maße erhalten bleiben, was im Pixelbereich auf Grenzen stößt. Was die Genauigkeit technischer Bauelemente ermöglicht, soll nicht durch ungenaue Rechnungen in Frage gestellt werden.
Nachdem das Original in geeigneter Form abgebildet ist, z.B. mit einer Stereokamera in Form
von zwei zweidimensionalen Pixelbildern, könnte daraus ein dreidimensionales Bild
berechnet werden.
Ein großes Problem entsteht durch die Tatsache, daß die Rasterungen von Urbild und Bild im allgemeinen nicht übereinstimmen. Es treten zwei Teilprobleme auf:
Sei f eine Abbildung zwischen zwei Pixelmengen, P und P' Pixel mit P Urbild, P' Bild. Dann
gibt es zwei Möglichkeiten zur Vorgehensweise:
Das helle Muster im skalierten Bild entsteht durch den durchscheinenden Hintergrund an Stellen, wo Pixeln des
Bildrasters kein Bild eines Urbildpixels zugeordnet wurde.
Besser wäre es, P' auf mehrere Pixel zu verteilen. Dies ist möglich, wenn wir jedes Pixel als Quadrat auffassen. Ein Pixel im Bildraster würde dann aus allen ihn überdeckenden Bildpixeln gemittelt, wobei als Gewicht der Überdeckungsanteil genommen würde. Es wäre eine relativ aufwendige Rechnung nötig.
Beide Methoden lösen nicht das Problem von Löchern im Bild.
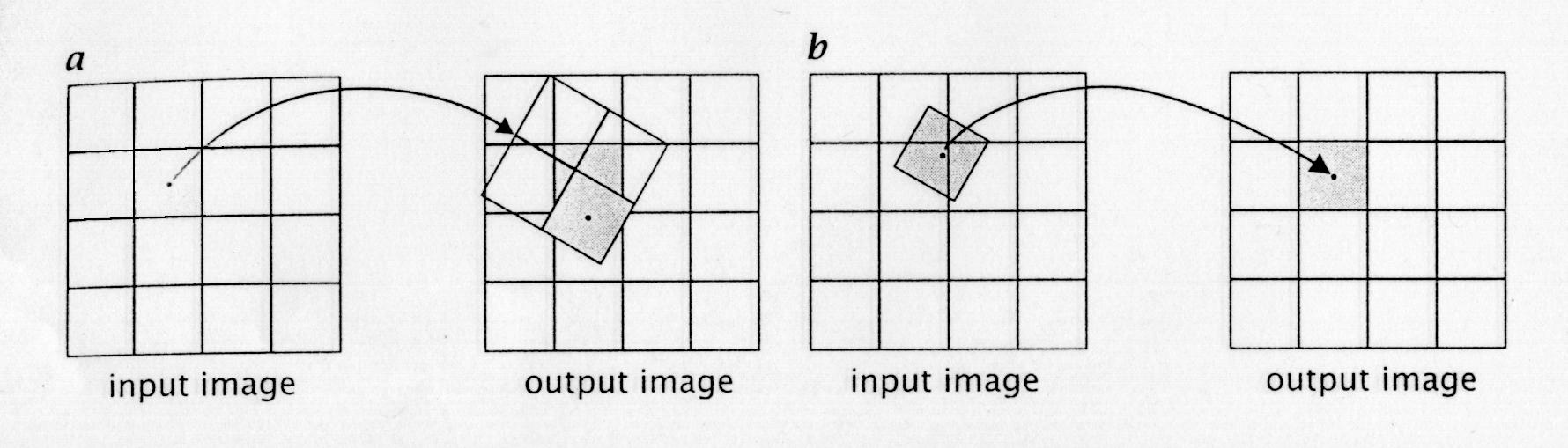
a) P' = f(P) Das Bild des Urbildrasters (schräg gezeichnet) deckt sich nicht mit dem Bildraster. Die vier Pixel
könnten zur Berechnung des Wertes des Bildpixels verwendet werden.
b) P = f -1 (P') Das Urbild des Pixels (schräg gezeichnet) berührt mehrere Urbildpixel.
Skalierung unter Verwendung der Methode der
Umkehrabbildung ohne Interpolation.
Es wird jeweils der Pixelwert des dem rechnerischen
Urbild am nächsten liegenden Pixels verwendet.
Daher treten im Bild keine Löcher auf.
|
| 
|
|
| Urbild | Translation | Skalierung |
| 
| 
|
| Dehnung | Scherung | Rotation |
Für eine affine Abbildung g, einen Vektor T und P, Q, k wie oben gilt:
Affine Abbildungen haben eine Reihe von nützlichen Eigenschaften, wie z.B. Parallelität zu
erhalten und können durch Matrizenrechnung berechnet werden.
v' = M * v + T ,
wobei v Urbild, v' Bild , M im R² eine 2x2-Matrix der linearen Abbildung, T Translationsvektor,
oder genauer:
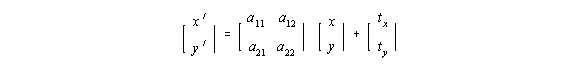
Diese Transformationen lassen sich auch mit nur einer Matrizenmultiplikation ausdrücken, wenn man zu homogenen Koordinaten übergeht.
Ein Punkt P im R² läßt sich durch genau einen Vektor v = (x, y) mit kartesischen Koordinaten darstellen. Bei Verwendung homogener Koordinaten wird eine Koordinate hinzugefügt. Ein Punkt entspricht dann einer ganzen Scharr von Vektoren v = k*(x ,y, 1). Wir verwenden den Repräsentanten (x, y, 1). Im R³ haben die Vektoren entsprechend eine Koordinate mehr.
Eine affine Abbildung läßt sich wie folgt berechnen:
v' = A * v ,
wobei v Urbild, v' Bild , A im R² eine 3x3-Matrix der affinen Abbildung
oder genauer:
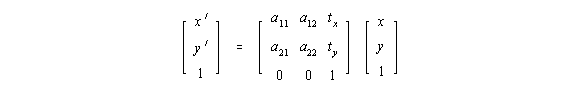
a11, a12, a21, a22 bestimmen den linearen Anteil der Transformation, tx und ty die Translation.
Auf diese Weise läßt sich also das Bild berechnen, wenn Urbild und Transformationsmatrix
gegeben sind.
Unter
www.inf.fu-berlin.de/~vratisla/Bildverarbeitung/Transfrm/Transfrm.html können mit diesem Applet verschiedene im Text
erwähnte Funktionen im Zweidimensionalen ausgeführt
werden.
Funktionalität:
Insgesamt läßt sich folgende Vektorgleichung aufschreiben:
X' = A * X ,
oder genauer
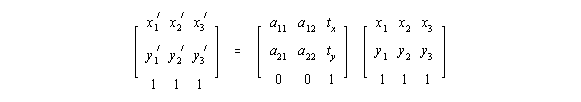
und auflösen nach : A = X' * X -1 .
Die inverse Abbildung läßt sich mit der inversen Matrix A -1 berechnen.
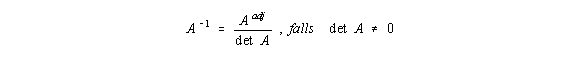
Für 3x3-Matrizen gilt:
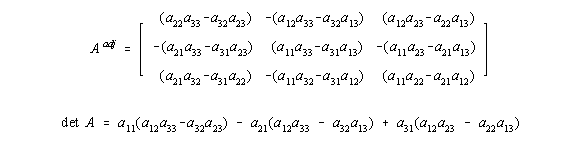
Allgemein lassen sich aus der Gleichung X' = A * X im Zweidimensionalen folgende
Formeln für die Berechnung der Bildkoordinaten gewinnen:
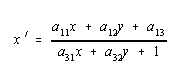
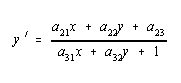
Für affine Transformationen fällt der Nenner weg, da a31 und a32 dann immer Null sind.
Abbildungen dieser Art sind durch vier Punkte mit ihren Bildern bestimmt. (Es gilt aber:
Nicht alle Abbildungen, die durch vier Punkte mit ihren Bildern gegeben sind, sind in
homogenen Koordinaten mit einer 3x3-Matrix darstellbar!)
| Abbildung mit der Matrix:
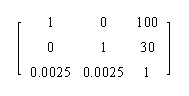 Parallelen bleiben nicht erhalten, dies ist keine affine Abbildung. (Die Löcher im Bild stammen lediglich von der Vorwärts-Abbildung.) |
Seien x ein Punkt und xm,n einer aus der Umgebung von x. 'm', 'n' beziehen sich dabei auf die
Position innerhalb des Filterkerns, angewendet auf x. G(xm,n) ist der Grauwert von xm,n:
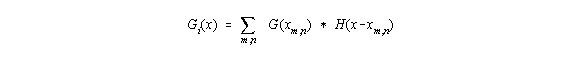
H ist dabei der verwendete Filterkern, Gi(x) der resultierende Grauwert an der Stelle i.
Gehen wir davon aus daß der Filterkern H separierbar ist, so läßt er sich in eindimensionale
Filterkerne zerlegen.
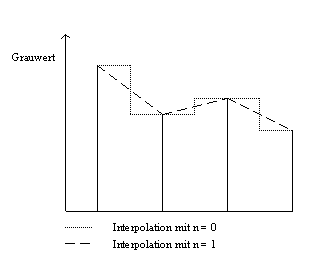
Ein höherer Grad gibt eine glattere Kurve, benötigt aber auch mehr Rechenzeit. Der einfachste Fall ist n=0. Hier werden überhaupt keine mittleren Werte berechnet, sondern die Werte der Stützstellen verwendet. Die "ausgleichende" Kurve besteht aus Konstanten und weist Sprünge auf, ist also nicht stetig. Diese Sprünge sind im Bild als Grauwertstufen zu sehen.
Bei Fall n=1 werden alle Punkte mit Geraden verbunden, wobei x=0 die zu interpolierende Stelle sei.
Sei dx der Abstand zweier benachbarter Punkte, so ergibt sich für -dx/2 < x < dx/2:
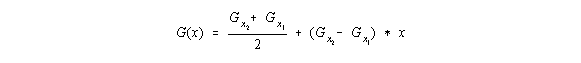
Für den Filterkern ergibt sich:
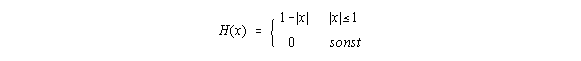
Die ausgleichende Kurve hat keine Sprünge aber Ecken an den Stützstellen, ist also stetig
aber nicht differenzierbar. Das Bild ist im Vergleich zum vorigen Fall wesentlich weicher.
Ab n=2 werden Parabeln verwendet.
Für n = 0 findet keine Interpolation statt, die
Punkte erhalten den Wert des nächsten Nachbarn.
Für n = 1 gibt es keine Sprünge, jedoch ist die Kurve in den Stützpunkten nicht stetig ableitbar.
Für n > 1 ergibt sich dann eine gebogene Kurve, bei erhöhtem Rechenaufwand.
Der Nachteil der Interpolation mit Polynomen ist,
daß nicht alle Ableitungen stetig sind.
Vergrößerung um Faktor 4 mit Verwendung der nächsten Nachbarn.
Jeweils vier Pixel in einer Zeile erhalten den gleichen Wert, wodurch ein Treppeneffekt zustande kommt.
Vergrößerung um Faktor 4. Die Pixelwerte errechnen
sich aus den Urbildpixeln mit ihren vier Nachbarn.
Dabei wird eine Art linearer Interpolation verwendet,
das arithmetische Mittel der Intensitäten der drei
Farbbestandteile. Der Treppeneffekt wird deutlich
geglättet. (Die Abstände zu den Nachbarn gehen in
diesem Beispiel nicht ein.)
Ein B-Spline ist eine ausgleichendeKurve um vorgegebene Punkte Pi und berechnet sich als
parametrisierte Kurve im Prinzip durch folgende Formel:
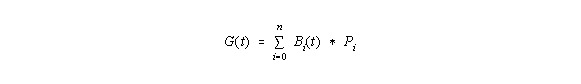
wobei t aus [0,1] und Bi(t) eine Gewichtung ist, die sich rekursiv berechnen läßt.
Die Bi(t) gehören einer zuvor zu definierenden Ordnung an, welche die Qualität der
Interpolation bestimmt. Bei Ordnung 1 werden die Werte der Nachbarpixel übernommen.
Ordnung 2 ist eine lineare Interpolation, d.h. die Punkte werden miteinander verbunden. Ab
Ordnung 3 resultieren ausgleichende Kurven. Bei B-Spline-interpolierten Bildern werden
ausreißende Grauwerte geglättet, da die Kurve nicht durch die Stützpunkte laufen muß.
B-Spline der Ordnung 4.
Ein Applet, das B-Splines erzeugt findet sich unter:
www.inf.fu-berlin.de/~vratisla/Bildverarbeitung/Bspline/Bspline.html.
Bei Verwendung eines Interpolationsfilters mit separierbaren, d.h. in eindimensionale Kerne zerlegbaren Filterkernen können zunächst alle Zeilen skaliert werden und dann erst die Spalten, was die Effizienz erhöht. Dazu können für jede Zeile dieselben Ortskoeffizienten genommen werden, was erheblich Rechenzeit spart.
Entsprechend werden im nächsten Schritt die Spalten skaliert.
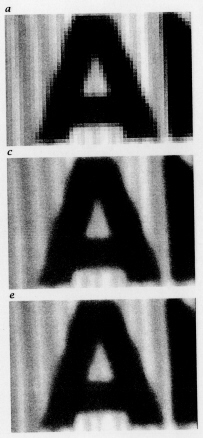
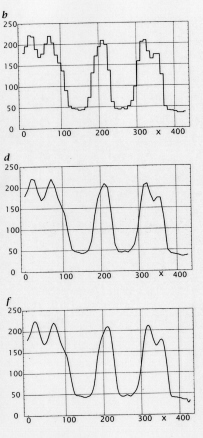Skaliertes Bild und ein Zeilenprofil:
a) Vergrößerung mit Interpolation der Ordnung 0, d.h. mit Übernahme der Nachbarpixel
b) Vergrößerung mit Interpolation der Ordnung 1, d.h. mit linearer Interpolation. (Verbinden der Pixelwerte durch Geraden)
c) Vergrößerung mit Interpolation der Ordnung 3, d.h. mit kubischer Interpolation (Polynome der Ordnung 3)
Bei Übernahme der Nachbarpixelwerte
entstehen Stufen. Die Interpolationen 1. und 3.
Ordrung sind kaum zu unterscheiden.
Eine Rotation ist zwar mit einer einzigen Matrizenmultiplikation möglich, dabei werden
jedoch Zeilen und Spalten zugleich transformiert. Es ist jedoch möglich, diese Operation mit
einer Reihe eindimensionaler Transformationen auszuführen, um sie mit den
eindimensionalen Filteroperationen koppeln zu können. Dazu kann man sich dreier
Scherungen bedienen:
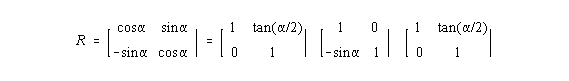
Scherungen können effizient zeilenweise ausgeführt werden, da wie bei der Skalierung für
jede Zeile die selben Koeffizienten verwendet werden können.
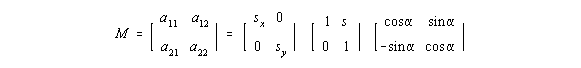
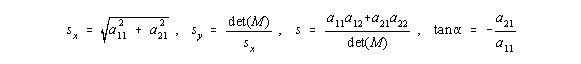
Effiziente Rotation zusammengesetzt aus drei
Scherungen.
www.inf.fu-berlin.de/~vratisla/Flug/Flug.html erreichbar.
Eine Landkarte wird dabei auf eine Kugeloberfläche projiziert, welche wiederum unter
Zentralprojektion auf den gedachten Bildschirm abgebildet wird.
| 
| 
|
| 
| 
|
Eine Bildfolge aus dem Applet www.inf.fu-berlin.de/~vratisla/Flug/Flug.html.